Raisonnement
Amélioré par J.-V. Aellen
Raisonnement : la vision classique
Introduction
Le raisonnement est un processus cognitif qui permet d'obtenir de nouveaux résultats ou de vérifier la réalité d'un fait en faisant appel soit à différentes lois soit à des expériences, quel que soit leur domaine d'application : mathématique, judiciaire, physique, pédagogie, etc.
On dit que l’individu effectue des inférences et que le mécanisme d’élaboration de ces inférences s’appelle raisonnement.
Déduction logique (raisonnement par déduction)
En logique, la déduction procède de la conception que les moyens ne sont pas plus importants que la fin (conclusion), par opposition à l'induction logique qui consiste à former des représentations générales à partir de faits particuliers. La déduction est un principe de la logique développée entre autres par Aristote. Ce dernier a en effet introduit une des formes les plus basiques du raisonnement déductif: le syllogisme. Un syllogisme comprends deux assertions que l'on appelle "prémisses" suivies par une troisième assertion, la conclusion.
D'autres théories logiques définissent le raisonnement déductif comme une inférence dont la conclusion est aussi certaine que les prémisses, tandis que dans un raisonnement inductif la conclusion peut être moins certaine que les prémisses. Dans les deux approches, la conclusion d'une inférence déductive découle des prémisses ; celles-ci ne peuvent être vraies si la conclusion est fausse. (En logique aristotélicienne, les prémisses d'un raisonnement inductif peuvent entretenir le même lien avec la conclusion.)
Exemples
Les syllogismes suivants sont valides :
Tous les Hommes sont mortels. Or tous les Athéniens sont des Hommes. Donc tous les Athéniens sont mortels.
La peinture est au-dessus du bureau. Le bureau est au-dessus du sol. Par conséquent la peinture est au-dessus du sol.
Le syllogisme suivant ne sont pas valides :
Tous les criminels sont contre le gouvernement. Or tous les membres de l'opposition sont contre le gouvernement. Donc tous les membres de l'opposition sont des criminels.
Ce dernier raisonnement est invalide, car les hypothèses ne parviennent pas à relier l'appartenance au parti de l'opposition et le fait d'être un criminel. Il s'agit d'une sorte de sophisme amené par un argument fallacieux : il confond certains « contre le gouvernement » (les membres de l'opposition, les criminels), et conclut sur une égalité entre tous ces individus particuliers sous prétexte qu'ils appartiennent à la même catégorie. Seulement, s'il est possible d'être à la fois membre de l'opposition et criminel, on ne peut en déduire que l'un implique nécessairement l'autre ; c'est ce que l'on appelle le sophisme du milieu non distribué (fallacy of the undistributed middle). Dans ce genre de cas, les deux prémisses peuvent être vraies sans que la conclusion soit correcte, car la forme logique est incorrecte.
Induction logique (raisonnement par induction)
L'induction est historiquement le nom utilisé pour signifier un genre de raisonnement qui se propose de chercher des lois générales à partir de l'observation de faits particuliers, sur une base probabiliste. Autrement dit, dans un raisonnement inductif, les premisses sont basées sur l'observation d'un cas, puis on généralise de ce cas particulier à une conclusion plus générale. Ainsi, pour le raisonnement inductif, les conclusions ne découlent pas des prémisses mais sont plutôt suggérées, avec des différents degrés de certitude.
Exemple
Remarque : Bien qu'associée dans le titre de cet article à la logique, la présentation qui suit correspond surtout à la notion « philosophique » de l'induction. En effet, en mathématiques, en logique et en informatique, l'induction complète, aujourd'hui très souvent abrégée en induction, est une autre façon de désigner la récurrence, aussi bien le raisonnement par récurrence que les définitions par récurrence. Le terme est souvent employé pour les généralisations de la récurrence aux bons ordres et aux relations bien fondées. En raisonnement automatisé, l'abduction est un mode de raisonnement qui vise à émettre une hypothèse pour expliquer un fait et elle ne doit pas être confondue avec l'induction présentée ici.
Par exemple :
Si la loi de la gravitation universelle détermine que, une pomme qui se détache de son arbre tombera sur le sol, et de quelle manière elle le fera, l'observation du mouvement de cette même pomme permet d'établir la loi générale, mais avec un degré de certitude très faible. Si ensuite, on observe que toutes les pommes et tous les corps tombent de la même façon, si on observe que les corps dans l'espace respectent la même loi, alors la probabilité de la loi augmentera jusqu'à devenir une quasi certitude. Dans le cas de la gravitation universelle, cependant, on a observé que l'orbite de Mercure présentait un effet de précession qui n'était pas expliqué par la loi. La loi de la gravitation universelle est cependant restée considérée comme universellement valide jusqu'à ce que Henri Poincaré explique le phénomène par une nouvelle loi de composition des vitesses qui conserve l'invariance de la vitesse de la lumière et qui sera expliqué par Einstein dans la théorie de la relativité restreinte. Malgré tout, la gravitation universelle reste utilisée car elle reste valable dans les cas courants, et elle est plus simple à utiliser et à comprendre que la théorie de la relativité.
Raisonnement inductif en sciences
Le raisonnement par induction constitue la procédure basique permettant de faire des découvertes scientifiques. En effet, l'objectif principal des sciences est de découvrir quelque chose de nouveau. Pour cela les scientifiques commencent souvent par des observations systématiques. En résumé, lorsque ces observations sont testées et qu'elles permettent de produire des résultats intéressants et significatifs, alors on peut les généraliser à une population plus large et parfois créer une théorie qui explique l'occurence de ces observations spécifiques. Dans ce cas le raisonnement inductif permet surtout de générer des hypothèses et ce sont ces hypothèses qui sont testées. Rappelons que la génération des hypothèses de recherche constitue véritablement la partie cruciale de la méthodologie scientifique!
Apprentissage de concept
L'apprentissage de concept, également connu sous les noms d'"apprentissage catégoriel", "atteinte de concept" (concept attainment), et "formation de concept", est largement basé sur les travaux du cognitiviste Jerome Bruner. Bruner, Goodnow et Austin (1967), ont défini l'apprentissage de concept comme la recherche et le listage des attributs qui peuvent être utilisés pour distinguer des exemplaires de non exemplaires d'une catégorie. En clair, les concepts sont les catégories mentales qui nous aident à classifier des objets, des événements, des idées, en se basant sur la compréhension du fait que chaque objet, événement, ou idée a un ensemble de traits caractéristiques. Par conséquent, l'apprentissage de concept est une stratégie qui requiert qu'un apprenant compare et différencie des groupes ou des catégories qui ont des caractéristiques pertinentes concernant le concept en question avec des groupes ou des catégories qui n'ont pas de telles caractéristiques.
L'apprentissage de concept se réfère également à une tâche d'apprentissage dans laquelle un humain ou une machine sont entraînés pour classer des objets en leur montrant des exemples d'objets avec leurs noms de classes. L'apprenant simplifie ce qui a été observé en considérant cela comme une forme d'un exemple (un exemplaire d'une catégorie). Cette version simplifiée de ce qui a été appris est ensuite appliquée à des exemples futurs. L'apprentissage de concept peut être simple ou complexe parce qu'il peut se faire dans de nombreux domaines différents. Quand un concept est difficile, il est moins probable qu'un apprenant soit capable de le simplifier, et, par conséquent il est moins probable qu'il apprenne. Couramment, cette tâche est connue comme "apprentissage à partir d'exemples". La plupart des théories sur l'apprentissage de concept sont basées sur le stockage d'exemplaires et évitent n'importe quel type de synthèse, ou d'abstraction.
Le rôle du raisonnement dans l'apprentissage des concepts
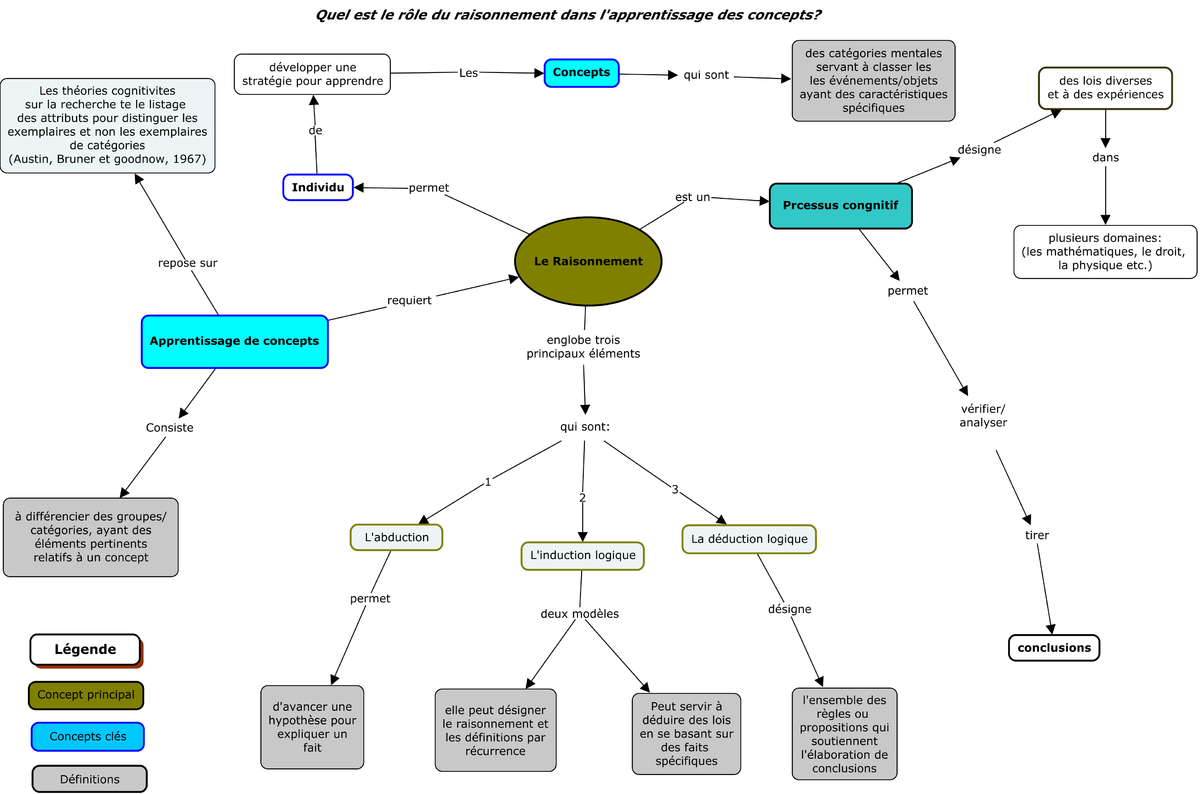
Ici, l'apprentissage de concepts fait référence à la construction de catégories. Dans ce processus de construction, chaque catégorie se définit par un ensemble de règles permettant d'inclure ou de rejeter un élément. On définit alors ce que sont les attributs nécessaires pour appartenir à la catégorie.
De ce fait, le raisonnement est employé pour construire des concepts. Ils s'expriment sous forme de catégories mentales qui acceptent ou rejettent des objets en fonction de leurs caractéristiques.
Comme indiqué, le processus cognitif qu'est le raisonnement s'appuie sur trois éléments principaux:
- l'abduction
- l'induction logique
- la déduction logique
Comme la déduction et l'induction logique sont déjà traitées dans cette page, seule l'abduction sera traitée ici. L'abduction est le "raisonnement par lequel on restreint dès le départ le nombre des hypothèses susceptibles d'expliquer un phénomène donné". Selon Pierce, elle est la seule forme de raisonnement "capable d'introduire des idées nouvelles" (p.95, Tiercin, 1993).
Types de concepts
Pas un concept. L'apprentissage de concept doit être distingué du fait d'apprendre en répétant quelque chose de mémoire ou en discriminant entre deux choses différentes (discrimination). Néanmoins, ces problèmes sont intimement reliés dans la mesure où le rappel mnésique de faits pourrait être considéré comme un processus conceptuel trivial où des exemplaires antérieurs représentant le concept sont invariants. De la même manière, alors que la discrimination n'est pas la même chose que le véritable apprentissage de concept, les processus de discrimination sont inclus dans l'affinement de concept par la présentation répétée d'exemplaires.
Concepts concrets ou perceptuels vs concepts abstraits
Concepts définis (ou relationnels) et concepts associés
Concepts complexes. Des notions telles qu'un schéma ou un script sont des exemples de concepts complexes. Un schéma est une organisation de concepts plus petits (ou de caractéristiques) qui est corrigé par de l'information en provenance de la situation pour aider à la compréhension. Un script quant à lui est une liste d'actions qu'une personne suit afin d'atteindre un but. Un exemple de script serait le processus d'achat d'un CD. Il y a dans ce cas un certain nombre d'actions qui doivent se produire avant le véritable acte d'achat du CD. Ainsi, le script fournit une séquence des actions nécessaires et un ordre correct pour ces actions afin de réussir à acheter le CD.
Méthodes pour apprendre un concept
Découverte: n'importe quel bébé découvre des concepts par lui-même, tel que le fait de découvrir que chacun de ses doigts peut être contrôlé individuellement ou que les personnes qui prennent soin de lui sont des individus. Bien que cela soit guidé par la perception, la formation du concept est plus complexe que le simple fait de mémoriser des perceptions.
Exemples: la généralisation, supervisée ou non à partir d'exemples pourrait amener à l'apprentissage d'un nouveau concept, mais la formation de concept est plus complexe qu'une simple généralisation à partir d'exemples.
Mots: Ecouter ou lire de nouveaux mots amène à l'apprentissage de concepts, mais la formation d'un nouveau concept est plus complexe que l'apprentissage d'une définition de dictionnaire. Une personne pourrait avoir formé au préalable un nouveau concept avant d'avoir trouvé un mot une phrase pour l'exprimer.
Comparaison d'exemplaires: Une autre manière efficace d'apprendre de nouvelles catégories et d'induire de nouvelles règles de catégorisation consiste à comparer un certain nombre d'objets quand leur relation catégorielle est connue. Ainsi, le fait de comparer deux exemplaires alors que l'on est informé que les deux appartiennent à la même catégorie permet d'identifier les attributs partagés par les membres de la catégorie, et illustre la variabilité à l'intérieur de cette catégorie. D'autre part, la comparaison de deux exemplaires, alors que l'on sait qu'ils appartiennent à des catégories différentes pourrait permettre une identification des attributs qui ont une valeur diagnostique. Il est intéressant de constater que les comparaisons à l'intérieur d'une catégorie, et entre deux catégories pourraient ne pas être équivalentes en termes d'efficacité pour connaître ces catégories. La capacité à utiliser l'une ou l'autre de ces formes d'apprentissage par comparaison est sujette à changement au cours de la petite enfance.
Invention: quand les hommes préhistoriques qui manquaient d'outils utilisaient leurs ongles pour racler la nourriture des animaux qu'ils avaient tués ou de melons fracassés, ils remarquèrent qu'une pierre cassée avait parfois un côté tranchant comme un ongle et était, par conséquent, adaptée au raclage de la nourriture. L'invention d'un nouvel outil pour éviter de se casser les ongles était un nouveau concept.
Problèmes théoriques
En général, les problèmes théoriques qui concernent l'apprentissage de concept sont les mêmes que ceux qui concernent l'induction logique. Ces problèmes sont traités dans de nombreuses publications, qui incluent la littérature sur les espaces de version, la théorie de l'apprentissage statistique, l'apprentissage PAC, la théorie de l'information, et la théorie algorithmique de l'information.
Résolution de problème
Pour plus d'informations, voir la page Résolution de problème dans l'edutechwiki.
Généralités
La résolution de problème consiste à utiliser des méthodes génériques ou "ad hoc", d'une manière ordonnée, afin de trouver des solution à des problèmes. Certaines des techniques de résolution de problème développées et utilisées en intelligence artificielle, en sciences informatiques, en ingénierie, en mathématiques, en médecine, etc. sont liées aux techniques de résolution mentale de problème étudiées en psychologie.
La carte conceptuelle ci-dessous détaille comment est décrite la résolution de problème par différents modèles.
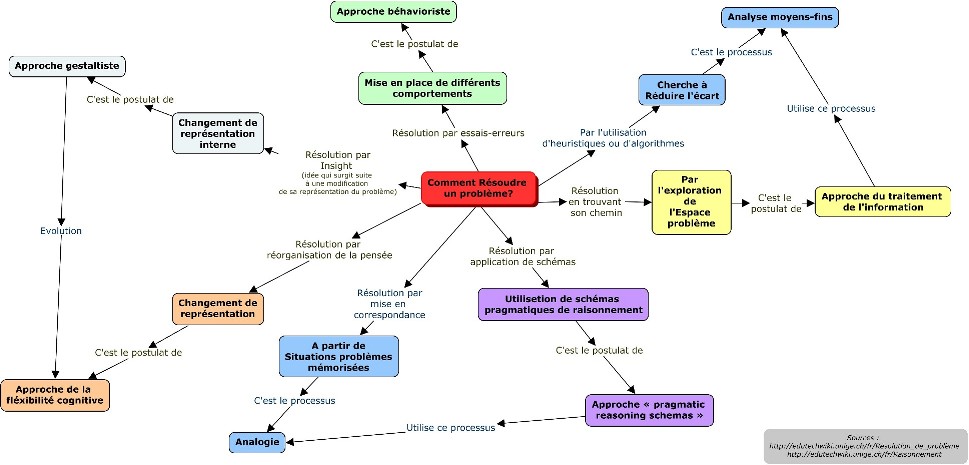
La carte conceptuelle ci-dessus renseigne sur différentes approches possibles permettant d'appréhender la résolution de problèmes.
L'approche béhavioriste postule que si l'un des comportements adopté permet la résolution de problème, alors celui-ci sera renforcé par les feedbacks reçus. Dans cette approche, la part inférentielle qui constitue le raisonnement n'est pas directement considérée puisque l'ajustement se fait par une répétitions de différents essais tant que l'erreur persiste.
L'approche gestaltiste puis, dans la continuité l'approche cognitiviste, indique que la résolution d'un problème s'opère par une modification de la représentation mentale. La pensée est amenée à être réorganisée jusqu'à ce qu'elle décrive adéquatement la situation.
Une résolution par analogie se traduit par le fait que le problème rencontré sera appréhendé en fonction des similarités qu'il partage avec des situations précédemment rencontrées.
L'approche des schémas pragmatiques de raisonnement s'appuie sur l'analyse des conditions. Ici, il n'est pas fait état d'une théorie générale du raisonnement puisque l'analyse est centrée sur le contexte. Les schémas pragmatiques sont issus de l'expérience et sont réactivés par le contexte (Cheng & Holyoak, 1985). Bien que comportant des similarités avec l'analogie, cette approche se différencie par l'existence de règles de permission ou d'obligation. Ces règles revêtent un caractère déontique puisqu'elles sont constituées de ce qui "peut ou doit être fait" (p.55, Grosset, Barouillet & Misuraca, 2004).
Dans une conception axée sur le traitement de l'information, le problème est vu comme un espace à travers lequel l'individu chemine. La résolution du problème se dessine alors comme l'exploration de cet espace. La rencontre du problème peut être vue comme l'entrée dans un labyrinthe. En empruntant le mauvais chemin le problème reste irrésolu, il y a alors lieu de revenir au précédent embranchement pour explorer une autre voie. Dans cette optique, le problème est résolu lorsque l'on parvient à sortir du labyrinthe.
L'allégorie du labyrinthe est intéressante puisqu'elle renvoie aux différentes stratégies employées pour en explorer les couloirs. Ceci nous amène à la notion d’algorithmes et d'heuristiques exprimés dans cette carte. Une stratégie heuristique se traduirait par une pérégrination moins systématique dans les couloirs du labyrinthe, la rapidité de sortie s'expliquerait alors partiellement par la chance. Dans l'algorithme, l'exploration diffère par son caractère systématique.
Stratégies de résolution de problèmes
Afin de résoudre les problème qu'il rencontre, les individus élaborent différentes stratégies. Ces stratégies de résolution de problème comportent plusieurs étapes. On appelle également cela le "cycle de résolution de problèmes" (Bransford & Stein, 1993). Dans ce cycle, la personne reconnaît le problème, définit le problème, développe une stratégie pour résoudre le problème, organise la connaissance concernant le problème, définit les ressources qu'elle a à disposition, contrôle ses progrès, et évalue l'exactitude de la solution au problème. On appelle cela un "cycle" parce qu'une fois qu'un problème est résolu, généralement, un autre apparaît. Voici quelques exemple de stratégies de résolution de problème :
- Abstraction: résoudre le problème grâce à un modèle du système avant d'appliquer la solution au système réel
- Analogie: utiliser une solution qui résout un problème similaire
- Brainstorming: (en particulier dans les groupes) suggérer un grand nombre de solutions ou d'idées, les combiner et les développer jusqu'à ce qu'une solution optimale soit trouvée
- Diviser et conquérir: diviser un problème complexe de grande taille en problèmes plus petits et plus faciles à résoudre
- Test d'hypothèses: supposer une explication possible au problème et essayer de la prouver
- Pensée latérale: approcher la solution indirectement et avec créativité
- Analyse des moyens et des buts: choisir une action pour chaque étape afin de s'approcher du but
- Méthode des objets focaux: faire la synthèse de caractéristiques qui n'ont apparemment pas de relation
- Analyse morphologique: évaluer le résultat et les interactions d'un système entier
- Preuve: essayer de prouver que le problème ne peut être résolu. Le point où la preuve ne marche pas sera le point de départ pour résoudre le problème
- Réduction: transformer le problème en un autre problème pour lequel il existe une solution
- Recherche: employer des idées ou adapter des solutions qui existent à des problèmes similaires
- Analyse de la cause première: identifier la cause d'un problème
- Essais et erreurs: tester les solutions possibles jusqu'à ce que la bonne soit trouvée
Le raisonnement comme outil de compréhension dans l'échange
Cette carte conceptuelle détaille la place du raisonnement dans l'échange entre l'émetteur et le récepteur d'un message:

Une utilité sociale du raisonnement est exprimée ici. Cette carte met en évidence deux composantes principales. La première est définie comme les maximes de conversation. Au nombre de quatre, elles visent à optimiser la bonne réception du message par l'interlocuteur. En respectant ces règles, l'émetteur minimise les risques "d'échec conversationnel" avec le récepteur. En d'autres mots, il limite les risques d’incompréhensions et favorise ainsi une possible coopération.
La deuxième composante principale réside dans le fait que le strict respect de ces règles n'est pas obligatoire et que la transgression d'une ou plusieurs de ces règles reste possible sans entrainer d'échec. Cette transgression possible est dictée par le contexte et l'implicature conversationnelle. Les opportunités de transgressions sont pertinemment illustrées par les exemples repris dans cette carte. L'exemple de la question sur Jean démontre parfaitement une situation de coopération réussie. La vidéographie nous renseigne sur le fait que la conversation peut être audible pour Jean. La réponse dénuée de pertinence du récepteur peut indiquer à l'émetteur que Jean est présent. Le but de la coopération est alors de ne pas se retrouver dans une situation conflictuelle avec Jean.
Pour mesurer pleinement la nécessité du respect de ces règles et les possibles transgressions, il y a lieu de ne pas limiter la définition de l'énoncé aux seuls mots qui le compose. L'énoncé doit également s'étendre à la dimension non verbale du langage.
Pour aller plus loin
- Anderson, J. R. (1982). Acquisition of cognitive skill. Psychological review, 89(4), 369. Article très long, début intéressant.
Références
- Anderson, J. R. (1983). A spreading activation theory of memory. Journal of verbal learning and verbal behavior, 22(3), 261-295.
- Grosset, N., Barrouillet, P., Misuraca, R. (2004). Développement du raisonnement conditionnel et tâche de sélection de Wason. In: L'année psychologique. vol. 104, n°1. pp. 51-81.
- Cheng, P. W., & Holyoak, K. J. (1985). Pragmatic reasoning schemas. IN: Cognitive Psychology, 17(4), 391–416.
- Michael R. Genesereth and Nils J. Nilsson, (1987) Logical Foundations of Artificial Intelligence, Morgan Kaufmann, chap. 7 Induction, pp. 161-176.
- Tiercelin, C. (1993). C.S. Peirce et le pragmatisme. Paris: Presses universitaires de France.
Créer une nouvelle sous-page production vidéographie
Ajouter une nouvelle production (MAX par promotion = 2)
Sous-pages qui existent déjà et (y compris des productions):
- Raisonnement/Adaptive Control Of Thought
- Raisonnement/Comment résolvons-nous un problème ?
- Raisonnement/Le Raisonnement
- Raisonnement/Les différentes stratégies de résolution de problèmes
- Raisonnement/Modèle mental
- Raisonnement/Production Sandrine Favre
- Raisonnement/Raisonnement dans l'apprentissage des concepts
- Raisonnement/Raisonnement et apprentissage de concepts
- Raisonnement/Selon Grice, comment le raisonnement permet-il aux hommes de se comprendre ?