« Projet de formation mathplusplus pour parents d'élève » : différence entre les versions
| Ligne 103 : | Ligne 103 : | ||
==== Pour en savoir plus ==== | ==== Pour en savoir plus ==== | ||
=== | === Une alternance présence/distance === | ||
==== Plus-value pour la formation ==== | ==== Plus-value pour la formation ==== | ||
L’alternance des activités, en présence et à distance, de la formation offre différents avantages. Par exemple: | L’alternance des activités, en présence et à distance, de la formation offre différents avantages. Par exemple: | ||
Version du 2 juin 2019 à 15:30
Rédigé par les étudiants du master MALTT dans le cadre du cours ADID2 : Mariana Mozdzer, Tatiana Timofeeva, Florian Ribon et Léonard Truscello
Juin 2019
Une formation mathématique pour parents
Contexte
Les parents des enfants du cycle d’orientation suisse se trouvent dans une situation difficile lorsqu’ils ont besoin d’aider leur enfants avec les devoirs en mathématiques. Bien souvent, ils peinent à se souvenir de leurs notions en mathématiques qui remontent à plusieurs années. Pour certains également, leur expérience des mathématiques à l’école n’a probablement pas toujours été plaisante. C’est pourquoi notre formation, conçue spécialement pour les parents des enfants qui entrent au cycle, permet, d’abord, de modifier positivement les souvenirs des expériences désagréables vécues par le passé, et ensuite, de revoir les bases des mathématiques du niveau cycle afin de pouvoir soutenir leur enfant dans sa formation. L’accent est mis notamment sur le partage émotionnel, les jeux de rôles ou encore les activités collaboratives. Les parents reçoivent également, au long de leur formation, des outils pédagogiques et métacognitifs qui facilitent les interactions et les explications mathématiques avec leur enfant.
Public cible
La population cible de cette formation sont les parents d’élèves du cycle d’orientation qui souhaitent apprendre, mieux comprendre ou rafraîchir les sujets de mathématiques que leurs enfants vont aborder.
Leurs objectifs et leurs motivations sont d’aider et soutenir leurs enfants. Les expériences personnelles des apprenants avec les mathématiques peuvent être assez hétérogène. D’un côté, ceux qui ont une mauvaise expérience à l’école et du mal à comprendre les bases de la pensée mathématique, et d’un autre, les anciens “bons élèves” qui doivent seulement faire une mise à jour de leurs connaissances pour s’assurer d’assister au mieux leurs enfants.
Objectifs pédagogiques
Les objectifs pédagogiques visées par la formation sont :
- Transformer positivement les émotions associées aux mathématiques et à son apprentissage.
- Maîtriser les connaissances de base en mathématiques du cycle d’orientation.
- Maîtriser des outils mathématiques, matériel ou formule, pouvant être utilisés dans la vie, professionnelle et privée, de tous les jours.
- Développer sa capacité d’explication de concepts appris, afin de les transmettre à son/ses enfant(s).
- Développer sa capacité à encadrer son/ses enfant(s) dans l’apprentissage de sujets complexes.
- Développer des compétences du 21ème siècle suivantes:
- - Numératie - par la réalisation d'exercices.
- - Pensée critique - par la conception collaborative des exercices.
- - Curiosité - par la fixation des objectifs individuels et communs.
- - Initiative - par le choix des thèmes/activités préférés.
- Développer sa capacité de collaboration autour d’un apprentissage et autour de la résolution de problèmes.
Description de la formation
Contenu et durée de la formation
La formation proposée est une formation hybride. Les dispositifs et activités de ce format s'articulent entre des phases de formation en présence et à distance (Peraya, Charlier et Dschryver, 2014).
La formation a une durée d’un mois et demande à l’apprenant d’investir au minimum 15 heures. Elle est divisée en 4 modules thématiques hebdomadaires à réaliser à distance et 2 séances en présentiel. La première séance en présence introduit l’apprenant à la méthodologie de travail pendant le cours et son syllabus. La deuxième séance clôt la formation par une discussion rétrospective de 30 minutes en classe, avant de passer à la séance suivante qui introduira le premier module de la formation suivante, si l'apprenant s'engage à la suivre.
Objectifs de la formation
L’objectif de Mathplusplus est d’offrir plusieurs formations au long de l’année et de traiter l’ensemble du contenu étudié pendant le cycle d’orientation. La formation a pour but aussi de favoriser l’échange entre les participants et ainsi faciliter le travail à distance.
Investissement attendu
L'accès aux ressources de la formation à distance est permanent. Idem pour les activités asynchrones, par exemple l'utilisation du forum. Concernant les activités synchrones ponctuelles, Mathplusplus n’a pas les ressources humaines nécessaires pour effectuer des permanences régulières, mais une courte permanence journalière peut-être fixée pendant la formation. La charge de travail hebdomadaire est estimée à 3 ou 4 heures.
Une fois la formation finalisée, les apprenants ont accès aux ressources du cours sans date limite, même s’ils ne sont pas inscrits à la formation suivante
Une approche pédagogique cohérente
Les 4 critères proposés par Boud et Prosser pour le design des formations en ligne ont guidé la conception des activités de cette formation (Molinari, 2018):
- L’engagement de l’apprenant, en tenant compte de ses connaissances initiales, de ses objectifs personnels et de ses attentes ;
- La prise en compte du contexte dans lequel l’apprentissage a lieu: le contexte personnel de l’apprenant, la situation d’apprentissage et le contexte institutionnel ;
- La mise au défi de l’apprenant en stimulant sa participation active ;
- L’inclusion d’une forte composante pratique, afin que l’apprenant puisse appliquer ce qu’il a appris.
Effectivement, la formation prend en compte en tout moment la situation particulière de sa population cible: les parents d'élèves cherchant des outils pour soutenir leurs enfants dans leur apprentissage. Les activités proposées ont été développées pour offrir pas seulement des connaissances en mathématique, mais aussi des techniques pour transmettre ces connaissances dans leur contexte familial. En favorisant la communication entre pairs, le travail collaboratif, la pratique et la reflexion à chaque étape, la formation vise à un apprentissage profond et intégral.
Cette approche est soutenu aussi par le modèle de “communauté d'enquête” développé par Garrison, Anderson et Archer suggère que les dispositifs d’apprentissage en ligne doivent permettre “le partage d’idées, information et opinions parmi les instructeurs et les apprenants” (Picciano, 2017, p.173) en s’appuyant sur 3 éléments: la “présence sociale” (la capacité des apprenants de participer dans la communauté d’apprentissage), la “présence de l’instructeur” comme facilitateur des processus cognitifs et la “présence cognitive” par laquelle les apprenants vont construire leur connaissance grâce à la réflexion (Bates, 2015). Dans ce cadre, les technologies à notre disposition ont été utilisées de manière à permettre les 7 affordances de Jeong (2016) pour la collaboration dans des environnements numériques: (1) l’engagement dans une tâche en commun, (2) la communication (3) le partage de ressources, (4) l’engagement dans des processus collaboratifs d’apprentissage, (5) l’engagement dans la co-construction, (6) le suivi et l’apprentissage régulé et collaboratif, (7) la construction de groupes et communautés. La formation a été développée avec LAMS (Learning Activity Management System) qui offre des outils pour la création des leçons et ses activités, comme un forum, un mindmap, le partage de ressources, etc. Pour compenser les limitations de LAMS, surtout pour les activités collaboratives, nous avons cherché des alternatives dans des applications externes.
De manières générales, la formation s’appuie sur les principes socio-constructivistes d’apprentissage par la résolution collaborative de problèmes. L’enseignant propose des problèmes dans un environnement social où l’apprenant trouve des solutions et construit ses connaissances grâce à l’interaction avec les autres (Picciano, 2017). Comme George et al (2013, p.9) l’indiquent, “les interactions avec les autres sont essentielles à l’apprentissage, qu’il s’agisse de coopérations, collaborations ou conflits socio-cognitifs”. L’instructeur joue un rôle central dans le processus de construction de connaissances, en tant que facilitateur actif et membre de la communauté d’apprentissage (Picciano, 2017).
Avec des activités comme la résolution d’exercices en groupe, la création de défis pour ses camarades, ou encore la participation aux divers forums, la formation suit une pédagogie active. Les activités rendent les apprenants acteurs de leur formation en servant de base à la construction de leur savoir. Les participants s’engagent dans un apprentissage actif et dynamique. Ils apprennent, d’une manière plus profonde, en agissant sur le contexte et le contenu étudié, ainsi qu’en interagissant avec les autres (George et al, 2013).
L’apprentissage expérientiel est un autre pilier de la formation. George (2013, p.9) le définit comme “un processus d’attribution de sens aux informations présentes dans une situation et d’extraction de ces sens au vue de les relier aux situations de tous les jours”. Les jeux de rôles, tant en présence comme à distance, mettent l’apprenant dans des situations proches de sa réalité de parent. L’objectif sera de l’aider à développer des compétences de tuteur en mathématiques, mais aussi de se mettre à la place de son enfant et de sa problématique.
Les sections suivantes décrivent en détail quatre composantes fondamentales de la formation : la collaboration à distance, l’engagement, le suivi et l'alternance présence/distance.
Une collaboration à distance orientée objectifs
Plus-value pour la formation
Dans cette formation, les parents révisent des notions mathématiques et apprennent à les transmettre à leur enfant. La formation propose de développer ces compétences de collaboration, communication et transmission de connaissances à travers ses différents modules, cohérentes avec ses objectifs d'apprentissage.
Les activités collaboratives proposées aux apprenants visent à promouvoir la construction des connaissances d’une manière active et participative. Cette collaboration est nécessaire dans les activités en groupe pour favoriser les compétences de discussion, d’entraide, d’organisation et de participation. Les activités collaboratives aident ainsi l’apprenant à devenir agent et acteur principal de son apprentissage. Ces activités, au regard de l’objectif principal d’aider son/ses enfant(s) à mieux comprendre les mathématiques, enseignent l’utilisation d’outils, pédagogiques et métacognitifs, pertinents.
Par exemple, en expliquant des notions mathématiques à ses camarades dans une activité collaborative, l'apprenant entraîne ses compétences d'entraide et pédagogiques, ainsi que sa compréhension des mathématiques.
Afin d'être cohérent avec les contraintes des apprenants, éducation des enfants et responsabilités professionnelles, les activités collaboratives sont généralement courtes, dynamiques et asynchrones. Par exemple, résolution d'exercices en groupe, discussion sur un forum ou encore construction d'un réseau sémantique sur une nouvelle notion mathématique. Les activités synchrones sont moins nombreuses et moins contraignantes au niveau du nombre de participants que les activités asynchrones. Par exemple, une session Skype entre deux apprenants pour l'explication d'une théorie ou un soutien pour expliquer la correction d'un exercice. Dans une classe d'une vingtaine d'apprenants, les probabilités de trouver du temps entre deux apprenants pour une courte vidéo-conférence est suffisamment élevée.
Pour en savoir plus
Jeong et Hmelo-Silver (2016, p. 247) font la différence entre la collaboration et la coopération. La collaboration demande aux apprenants de s’engager à travailler ensemble pour accomplir une tâche d’apprentissage tandis que la coopération indique plutôt une séparation de tâches dont les résultats sont ensuite combinés. La formation de Mathplusplus incite essentiellement l’apprenant à la collaboration et au développement d’une conscience de groupe déclenchant des processus d’apprentissage positifs (Bodemer, 2018).
Selon Bates (2015, p.143), l'apprentissage collaboratif en ligne, s’il est bien encadré, peut favoriser l’apprentissage profond et le développement des compétences comme : “la pensée critique, la pensée analytique, la synthèse et l’évaluation”. Harasim (2018) explique que la collaboration en ligne se déroule en trois phases dont l’instructeur a un rôle fondamental comme participant et facilitateur: la génération d’idées, l’organisation d’idées et la convergence intellectuelle. Dans cette dernière phase, “les membres du groupe atteignent un niveau de synthèse intellectuelle, c’est-à-dire, ils comprennent et parviennent à un consensus ou accepte d’être en désaccord. Si la discussion nécessite une position ou un seul résultat, tel qu'un projet commun, un essai commun ou une activité coproduite, l'équipe doit parvenir à un consensus opportun sur ce qu'elle va faire, comment et quand.” (Harasim, 2018, p.8).
Engagement
Plus-value pour la formation
Les exercices et les activités de la formation favorisent l'autonomie et l'autorégulation des apprenants. Ceux-ci font leur propre choix d'apprentissage, i.e. ils sont autodéterminés. Le module 0 est, par exemple, conçu sur la base de l'autodétermination (SDT ci après) afin de créer une atmosphère bienveillante et propice à l’apprentissage, en présence et à distance, et d’augmenter les deux types de motivation: intrinsèque et extrinsèque. Ces différents éléments favorisent l'engagement des apprenants dans la formation.
Afin de favoriser la motivation intrinsèque, les éléments suivants sont mis en avant lors du module 0.
Le renforcement de la relation sociale se construit grâce au partage émotionnel. Afin de créer de l’engagement de la part des apprenants, il est important d’encourager les apprenants à partager leurs ressentis (positifs ou négatifs) par rapport à leur expérience précédente de l’apprentissage des mathématiques, leurs peurs ou leurs sentiments. La fonction du tuteur est alors de susciter de la curiosité et de l’intérêt envers la matière afin de favoriser la transformation positive de la perception des mathématiques; d’une expérience négative du passé à une expérience positive du présent.
Le renforcement du sentiment de compétence se construit sur la base de la reconnaissance des expériences précédentes des apprenants. Lorsque l’expérience pré-existante est mise en évidence par le tuteur et est valorisée par les collègues du groupe, cela permet de stimuler davantage la motivation intrinsèque. Par exemple dans le module d'introduction, les apprenants partagent leur sujet préféré et celui qu'ils maîtrisent le mieux. ils sont ensuite valoriser comme expert du domaine par leur tuteur, puis engagés auprès de leurs camarades par cette responsabilité d'expert.
Le renforcement de l’autonomie assuré par le choix d’objectifs propres à chaque apprenant. Le degré d’autonomie est particulièrement renforcé, étant donné que les apprenants, non seulement, font leur propre choix d’objectifs, mais ils précisent également la contrepartie. En d’autres termes, le temps et les ressources qu’ils sont prêts à consacrer pour atteindre leurs buts et la date d'achèvement visée.
Enfin le renforcement de la motivation extrinsèque prend place aux travers du groupe. En effet, les apprenants sont invités à fixer les objectifs communs du groupe, afin de développer une co-régulation.
(Les sentiments d’accomplissement sont favorisés davantage, alors que les sentiments d’incompétence, de contrôle, d’anxiété ou la culpabilité sont évités. → à préciser plus clairement)
Pour en savoir plus
L’engagement des apprenants se fonde sur l’usage des éléments constituant la base de la théorie de l’auto-détermination : la compétence, l’autonomie et la relation sociale
Suivi
Plus-value pour la formation
Le suivi des apprenants se fonde sur les processus métacognitifs. Le but d’un suivi “intelligent” est d’organiser une régulation et une auto-régulation régulière consciente, et non pas une régulation externe, par exemple par un tuteur. Les activités proposées dans un environnement éducatif bienveillant laissent aux apprenants la liberté d’organiser leur apprentissage, individuel et collaboratif. Le suivi permettra de tracer les activités des apprenants afin qu’ils sachent où il se trouvent et de contextualiser ce qu’ils font. Les traces d’activités sont indispensables pour les acteurs de la formation. Le suivi est organisé de deux manières. D’une part, par un système de guidage, pendant les activités, qui offre une vue globale des étapes d’apprentissage. De plus, une vue d’ensemble des activités accomplies permet à l’apprenant de déclencher les processus réflexifs sur ce qui a été réalisé. Ainsi, les traces servent de rappel des activités, de leur processus de réalisation et de suivi du déroulement des activités. D’une autre part, au moyen de la co-régulation générée par les objectifs individuels et de groupe fixés lors du module 0. L’interaction entre pairs favorise l’auto-régulation et le travail collaboratif favorise la régulation.
Les outils de suivi permettent de faire un suivi régulier et qualitatif durant la totalité de la formation et de manières diverses: une liste de tâches que oblige à l'apprenant à cocher les activités réalisées après chaque unité thématique avant de passer à l'activité suivante, un sommaire des activités achevées est présenté à la fin de chaque unité, des exercices formatifs avec de feedback immédiat ou encore la participation aux forums. Cette dernière sert à tracer les questions ou les difficultés rencontrées lors de réalisation d’exercices, de tâches individuelles ou de groupe. Un "Grade Book" permet à l'enseignant de suivre le progrès de chaque apprenant.
Pour en savoir plus
Une alternance présence/distance
Plus-value pour la formation
L’alternance des activités, en présence et à distance, de la formation offre différents avantages. Par exemple:
- La flexibilité, elle est indispensable étant donnée les obligations personnelles et/ou professionnelles du public cible.
- Le mode d’activités de groupe synchrone et asynchrone: le travail en présence favorise des activités plutôt synchrones, alors que le travail à distance peut alterner les deux modes synchrone et asynchrone grâce aux outils proposés.
- La présence d’interactions sociales (tuteur-apprenants et apprenants-apprenants). Elle garantie un support technique et un soutien psychologique et cognitif nécessaires pour un travail à distance. Engagés dans une activité de collaboration à distance, les apprenants communiquent avec des outils numériques proposés (chat, vidéoconférence) et évitent le sentiment d’isolement. Les interactions entre les apprenants se composent de confrontations et de négociations, en d’autres termes des conflits cognitifs, qui constituent un apprentissage collaboratif, selon la théorie socio-constructiviste.
- L’hybridation de la formation intègre les configurations propres à chaque format : en classe ou en ligne. Chaque module, indépendamment du format, définit avant tout des objectifs à atteindre, des acteurs, des activités, la médiation et des outils. Les dimensions socio-affective, cognitive, et pédagogique, présentes dans ces éléments, favorisent la participation active des apprenant.
Pour en savoir plus
Un usage vidéo motivant
Plus-value pour la formation
Afin de pouvoir étudier les notions mathématiques chez soi et sans contraintes, la formation a besoin d'un support pédagogique, de bonne qualité, accessible à tout moment. La vidéo, en tant que cours enregistré, répond à cette exigence. De plus, lorsqu'elle est bien faite, elle motive et dynamise l'apprentissage du contenu présenté.
Avec le développement des plateformes de streaming, la présence de vidéos d'apprentissage sur les mathématiques a explosé. Pour les étudiants, c'est devenu un outil d'apprentissage complémentaire à celui proposé par les enseignants de l'école obligatoire. En utilisant la vidéo comme support d'apprentissage pour les parents d'enfants, cela les prépare à rechercher ce type de support d'apprentissage. Ils pourront, par la suite, soutenir leur enfant en les aidant à s'autonomiser en cherchant du matériel pour compléter les supports pédagogiques donnés par leur enseignant.e.
Pour expliquer un concept, ici en mathématique, il ne suffit pas de le comprendre. Il faut être capable de synthétiser l'information et de présenter l'information le plus simplement possible. Ceci nécessite de l'entraînement. Dans la formation, les apprenants doivent aider les camarades qui ont des difficultés sur un sujet d'apprentissage ou qui sont en train de découvrir un sujet déjà maîtrisé. La vidéo est ici doublement utilisée. Premièrement en faisant des vidéos-conférences pour mettre en relation deux apprenants, lorsqu'ils s'entraident. Deuxièmement, en enregistrant ces vidéos conférences afin de les partager avec l'ensemble de leurs camarades, en présence par exemple, dans le but discuter et d'améliorer les compétences pédagogiques des apprenants.
Pour en savoir plus
L'utilisation de la vidéo comme outil d'instruction s'appuie sur les principes de la théorie cognitive de l'apprentissage multimédia de Mayer (2010). L'apprentissage multimédia est l'apprentissage par des mots, soit à l'oral ou à l'écrit, et des images, soit des animations, photos ou vidéos. L'apprenant utilise les canaux visuel et auditif pour intégrer d'une manière active et efficace l'information transmise en trois étapes: La sélection des éléments importants, l’organisation et l’intégration avec des connaissances antérieurs. Selon ce modèle, pour aider ce processus cognitif, une présentation multimédia ou vidéo doit suivre 7 principes: les contiguïtés temporelle et spatiale, la modalité, la cohérence, la redondance, les différences individuelles et l'utilisation d'images.
De nouvelles compétences indispensables aujourd'hui
Plus-value pour la formation
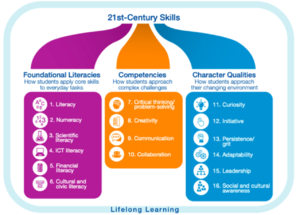
Le Forum économique mondial ou forum de Davos a écrit un rapport sur les compétences clés, dont la société du 21ème siècle aurait besoin. Le rapport décrit seize compétences.
La formation mathplusplus pour parents d'élève a l'avantage d'enseigner et de développer des compétences chez les parents d'élèves, mais aussi indirectement aux élèves par la transmission et le soutien de leurs parents. Transmettre au sein de la formation des compétences clés a ainsi le double avantage de servir les individus d'une famille et d'une manière plus globale la société.
Les mathématiques présentées permettent aux familles d'utiliser les nombres et l'algèbre pour établir des relations entre des quantités (numératie). En comprenant le fonctionnement de ces relations, il est possible à partir d'une situation de la vie réelle d'identifier un problème et de l'exprimer sous une forme mathématique afin d'en trouver la solution (résolution de problème).
Afin de soutenir son enfant, les apprenants s'exercent, dans la formation, à transmettre du contenu en réfléchissant à la manière de l'expliquer (communication). Ils doivent créer des nouveaux problèmes et imaginer de nouvelles situations (créativité).
Déjà mentionnée précédemment, les apprenants doivent travailler ensemble pour comprendre la théorie et résoudre différents problèmes (collaboration). Ils choisissent ensemble les sujets qu'ils souhaitent aborder et la manière dont ils souhaitent s'engager et collaborer (initiative). En interagissant, ils se questionnent et s'interroge entre eux ou avec leur tuteur pour essayer de comprendre le sujet (curiosité).
Pour en savoir plus
Le Forum économique mondial publie régulièrement différents rapports sur des problématiques globales. Voici le lien vers le rapport sur les compétences du 21ème siècle.
Déroulement de la formation
Séance d'introduction
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Évaluation |
|
| Résultats d'apprentissage |
|
| Ressources |
|
| Outils et médias |
|
Premier module
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Evaluation |
|
| Résultats d'apprentissage |
|
| Ressources utilisées | |
| Outils et médias |
|
Illustration du scénario du module
- Mathplusplusmodule1.png
Séquence LAMS du module 1
- Mathplusplusmodule1collab.png
Séquence LAMS partie collaborative du module 1
Deuxième module
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Evaluation |
|
| Résultats d'apprentissage |
|
| Ressources utilisées | |
| Outils et médias |
|
Illustration du scénario du module
- Mathplusplusmodule2.png
Séquence LAMS du module 2
- Mathplusplusmodule2collab.png
Séquence LAMS partie collaborative du module 2
Troisième module
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Évaluation |
|
| Résultats d'apprentissage |
|
| Ressources utilisées | |
| Outils et médias |
|
Illustration du scénario du module
- Mathplusplusmodule3.png
Séquence LAMS du module 3
- Mathplusplusmodule3collab.png
Séquence LAMS partie collaborative du module 3
Quatrième module
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Évaluation |
|
| Résultats d'apprentissage |
|
| Ressources utilisées | |
| Outils et médias |
|
Illustration du scénario du module
- Mathplusplusmodule4.png
Séquence LAMS du module 4
- Mathplusplusmodule4collab.png
Séquence LAMS partie collaborative du module 4
Séance de clôture
Présentation du module
| Titre |
|
|---|---|
| Format |
|
| Durée |
|
| Introduction |
|
| Objectifs pédagogiques |
|
| Contenu pédagogique |
|
| Approche pédagogique |
|
| Compétences du 21e siècle |
|
| Activité individuelle |
|
| Activité collaborative |
|
| Évaluation |
|
| Résultats d'apprentissage |
|
| Ressources |
|
| Outils et médias |
|
Références
Bibliographies
- George, S, Michel, C. & Ollagnier-Beldame, M. (2013). Usages réflexifs des traces dans les environnements informatiques pour l'apprentissage humain, en Intellectica, 2013/1, 59, pp., Association pour la Recherche Cognitive
- Jeong, H. & Hmelo-Silver, C. (2016). Seven Affordances of Computer-Supported Collaborative Learning: How to Support Collaborative Learning? How Can Technologies Help?, Educational Psychologist, 51:2, 247-265
- Mayer, R. (2010). Apprentissage et technologie. In Dumont, H., Istance, D., Benavides, F. (eds.) Comment apprend-on? La recherche au service de la pratique, OECD, Paris, pp. 191-209
- Molinari (2018) Le design pédagogique des environnements informatisés d’apprentissage, matériel du cours ADID1, MALTT, Tecfa, Université de Genève
- [1] Bates, A. W. (2015). Teaching in a Digital Age: Guidelines for Designing Teaching and Learning, BCcampus.
- Bodemer, Daniel & Janssen, Jeroen & Schnaubert, Lenka. (2018). Group Awareness Tools for Computer-Supported Collaborative Learning (disponible sur Moodle, cours ADID)
- [2] Harasim, L. (2018). Learning about Learning Online: The Methodology of Discourse Analytics. In B. Khan, J.R. Corbeil, and M.E. Corbeil (Eds.) Responsible Analytics and Data Mining in Education. Routledge
- [3] Picciano, A. (2017) Theories and Frameworks for Online Education: Seeking an Integrated Model , in Research Gate, référencé le 22 mai 2019.
- Carole Raby, Thierry Karsenti, Hélène Meunier and Stéphane Villeneuve (2011) Usage des TIC en pédagogie universitaire : point de vue des étudiants
- Mitchell, R., Schuster, L., Jin, H. S. (2017) Gamification and the impact of extrinsic motivation on needs satisfaction: Making work fun? in Journal of Business Research https://doi.org/10.1016/j.jbusres.2018.11.022
- Kusurkar, R. A., Croiset, G. & Ten Cate O. Th. J. (2011) Twelve tips to stimulate intrinsic motivation in students through autonomy-supportive classroom teaching derived from Self-Determination Theory in Medical Teacher, N° 33, pp. 978-982
- Ryan, R. M., Deci, E. L. (2000) Self-Determination Theory and the Facilitation of Intrinsic Motivation, Social Development, and Well-Being in American Psychologist, Vol. 55, N°1, pp. 68-78
- Smit, K., de Brabander, C. J., Boekaerts, M., Martens, R. L. (2017) The self-regulation of motivation: Motivation strategies as mediator between motivational beliefs and engagement for learning in International Journal of Educational Research, N°82, pp. 124-134
- Quintin, J-J. (2014), Design pédagogique d'un environnement de formation à distance, Université de Lyon
- Charlier, B., Deschryver, N., Peraya, D. (2004). Articuler présence et distance, une autre manière de penser l’apprentissage universitaire in L’AIPU: 20 ans de recherches et actions pédagogiques: bilans et perspectives, Université Cadi Ayyad
- Jégégou, A. (2010/2). Créer de la présence à distance en e-learning: Cadre théorique, définition, et dimensions clés in Lavoisier “Distance et savoirs”, Vol.8, pp. 257-274