Principes de base d'analyse statistique
| Manuel de recherche en technologie éducative | |
|---|---|
| Module: Analyse de données quantitatives | |
| ◀▬▬▶ | |
| ⚐ brouillon | ☸ débutant |
| ⚒ 2020/03/05 | |
Introduction
Ce petit chapitre vise à faire deux choses:
- Expliquer ce qu'est - au fond - un modèle statistique
- Présenter une simple typologie d'analyses.
Trouver la structure
Le but de l’analyse statistique est relativement simple: trouver/révéler une structure dans les données. Une structure est normalement définie par un croisement entre 2 variables (par exemple tableau, histogramme par catégories, ou nuage de points) ou par plusieurs variables.
Ce principe peut être exprimé par trois formules synonymes :
DONNÉES = STRUCTURE + NON-STRUCTURE
DONNÉES = VARIANCE EXPLIQUÉE + VARIANCE NON EXPLIQUÉE
DONNÉES = RELATION + VARIANCE NON EXPLIQUÉE
Exemple: analyse de régression simple
DONNÉES = droite de régression prédite + résidus (données non expliquées)
L’analyse de régression cherche à établir une droite qui permettra de maximiser la prédiction et de minimiser les résidus comme l'illustre la figure suivante:
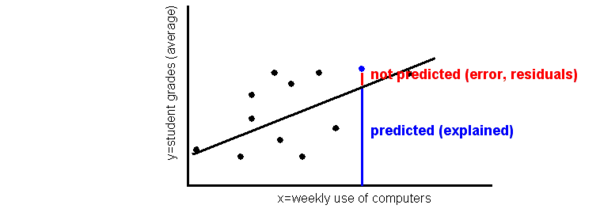
Attention: La structure est différente pour chaque type d'analyse statistique: Pour la corrélation, il s'agit d'un simple nombre, pour la régression il s'agit d'une formule pour une droite, etc.
Etapes de l’analyse statistique
Voyons à présent ce que nous entendons par analyse statistique et ce que vous devez faire dans ce cas. Dans ce chapitre, nous allons nous intéresser aux étapes qui suivent les premiers points de l’analyse:
Tableau 1: Principales étapes de l’analyse statistique
(1) Nettoyez vos données
- Assurez-vous que vos données soient correctes (e.g. vérifiez la transcription des données)
- Assurez-vous que les valeurs manquantes (e.g. les questions d’un questionnaire sans réponse) soient clairement identifiées comme des données manquantes
(2) Faites en sorte d’en connaitre davantage sur vos données
- Dressez des listes de données (uniquement pour les petits ensembles de données!)
- Etablissez des statistiques descriptives, e.g. des moyennes, des écarts-types, des valeurs minimales et maximales pour chaque variable
- Etablissez des graphiques, e.g. des histogrammes ou des boîtes à moustaches qui montrent la distribution
(3) Produisez des échelles composées
- E.g. créez une seule variable en calculant la moyenne à partir d’un ensemble de questions
- Testez si si cette nouvelles variable satisfait des exigences au niveau de la consistance/fiabilité (par ex. alpha de Cronbach)
(4) Examinez la distribution
- Décidez si la distribution des variables satisfait les hypothèses sur les données.
- Vous pouvez reprendre les opérations du point (2) mais aussi ajouter des coefficients statistiques comme les mesures asymétrie ou de normalité
(5) Etablissez des graphiques ou des tableaux qui présentent les relations
- E.g. créez des graphiques pour les données à intervalles (comme dans notre exemple précédent) ou créez des tableaux croisés
(6) Calculez des coefficients qui mesurent la force et la structure d’une relation
- Exemples de force: le V de Cramer pour les tableaux croisés, ou le R de Pearson pour les données à intervalles
- Exemples de structure: coefficient de régression, tableaux des moyennes dans l’analyse de variance.
(7) Calculez des coefficients qui décrivent le pourcentage de la variance expliquée
- E.g. R2 dans une analyse de régression ou Eta2 dans l’analyse de variance
(8) Calculez le seuil de signification, i.e. déterminez si vous êtes en droit d’interpréter la relation
- E.g. Chi2 pour les tableaux croisés, le F de Fischer dans l’analyse de régression
- Le seuil de probabilité est un chiffre entre 0.0 (bon) et 1 (souvent affiché sous "Sig." ou "p")
Remarque: avec un bon programme d’analyse de données statistiques, il est facile d’effectuer plusieurs étapes en une opération.
Types de coefficients statistiques
Chaque analyse statistique produit différents types de coefficients, i.e. des chiffres qui résument certains types d’information. Assurez-vous toujours d’utiliser uniquement des coefficients appropriés pour vos données. Il y a quatre types principaux de coefficients, que vous trouverez dans la plupart des méthodes d’analyse:
| Type de coefficient | |
|---|---|
| 1. Force d’une relation | Les coefficients vont généralement de -1 (relation négative totale) à +1 (relation positive totale). 0 signifie aucune relation. |
| 2. Structure (tendance) d’une relation | Résume une tendance |
| 3. Pourcentage de variance expliquée | Indique le degré de structure de votre modèle |
| 4. Seuil de signification de votre modèle | Calcule la probabilité ("Sig." / "p") que votre relation soit une distribution hasardeuse, i.e. qu’il n’y ait pas de relation entre les variables.
Typiquement, en sciences sociales, un seuil de signification inférieur à 5% (0,05) est acceptable. N’interprétez pas de données qui se situent au-dessus! |
Au delà de ces coefficients qui résument des relations vous devez aussi veiller à respecter les hypothèses sur les données, donc par exemple montrer que des variables utilisés dans une analyse "paramétrique" (corrélation de Pearson, Anova, etc.) possède une distribution proche de la normale. Ces quatre types sont mathématiquement liés: e.g., le seuil de signification ne dépend pas uniquement de la taille de votre échantillon, mais également de la force d’une relation.
Aperçu des méthodes statistiques
Les méthodes d’analyse de données statistiques peuvent être catégorisées en fonction des types de données (concept expliqué dans Statistiques descriptives et échelles). Le tableau ci-dessous présente des méthodes d’analyse bivariée courantes pour une variable X (explicative) indépendante et pour une variable Y (à expliquer) dépendante.
| Variable Y dépendante | |||
|---|---|---|---|
| Quantitative (à intervalles, échelle) | Qualitative (nominale ou ordinale) | ||
| Variable X indépendante (explicative) | Quantitative | Corrélation et régression | Transformez X en une variable qualitative et faites un tableau croisé (c.f. ci-dessous)
Alternativement, vous pouvez vous renseigner sur l'analyse discriminante ou la régression logistique. |
| Qualitative | Analyse de variance (aussi appelée Anova, Anova simple, comparaison de moyennes) | Tableaux croisés (aussi appelé tri croisé ou tableau de contingence | |
Un tableau similaire peut être créé pour une analyse multivariée, mais nous n’allons pas présenter ce sujet.
| Variable(s) Y dépendante(s) | |||
|---|---|---|---|
| Quantitative (à intervalles) | Qualitative (nominale ou ordinale) | ||
| Variable(s) X indépendante(s) (explicative) | Quantitative | Analyse factorielle, régression multiple, SEM, analyse typologique | Transformez X en variables qualitatives et reportez-vous ci-dessous ou séparez une variable en plusieurs variables dichotomiques (oui/non) et reportez-vous à gauche. Analyse discriminante pour une seule variable dépendante. |
| Qualitative | Anova | Positionnement multidimensionnel, logit, etc. | |
Hypothèses de données
Les hypothèses de données (Angl.: "Data assumptions") vous disent si oui ou non un méthode statistique est appropriée par rapport à un type de données. Savoir distinguer entre variables intervalles, ordinales et nominales est la chose la plus importante, mais il existe des contraintes supplémentaires. Les analyses "paramétrique" comme la régression, la corrélation de Pearson et la régression exigent que les données soient proches d'une distribution normale. Cela implique par exemple qu'on ne peut faire une régression avec une variable dichotomique (par exemple, 1=réussite et 2=non-réussite).