Analyse de régression et corrélations de Pearson

Manuel de recherche en technologie éducative
Module: Analyse de données quantitatives
◀▬▬▶
⚐ brouillon	☸ débutant
⚒ 2020/03/23

Le principe de la régression et de la correlation de Pearson

Nous avons déjà présenté le principe de la régression linéaire. Il permet de calculer une tendance entre une variable explicative X et une variable à expliquer Y. Ces variables doivent toutes deux être des variables quantitatives.

L’analyse de régression cherche à établir une droite qui résume l'évolution de Y en fonction des valeurs de X. Cette droite maximise la prédiction (linéaire) minimise les résidus. Nous avons déjà introduit la figure suivante dans le chapitre d'introduction aux analyses quantitatives

Structure d'une régression linéaire (la droite)

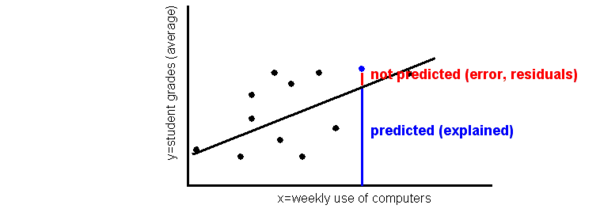
DONNEES = droite de régression prédite + résidus (données non expliquées)

Régression et coefficients de corrélation

• Ces coefficients de régression synthétisent le modèle, i.e. ils décrivent mathématiquement la droite.

Y = A + X * B

• B représente la pente de la droite
• A est une constante et représente l’écart par rapport au 0

Il existe ensuite 2 coefficients qui mesurent la relation et la portée du modèle:

• La corrélation de Pearson (r) synthétise la force de la relation
• R au carré (R²) représente la variance expliquée

Exemple: Age de l’enseignant et activités en dehors de la classe

Nous souhaitons répondre à la question: l’âge de l’enseignant explique-t-il les activités d’exploration en dehors de la classe? I.e. est-il plus probable que ce soient des enseignants plus âgés qui organisent des activités en dehors de la classe?

• Variable indépendante X: âge de l’enseignant
• Variable dépendante Y: fréquence des activités d’exploration organisées en dehors de la classe

Le résumé du modèle de régression produit par SPSS est présenté de la façon suivante. Nous pouvons observer qu’il existe une faible corrélation (R=0.316) et que la relation est significative (.027)

Age de l’enseignant et activités d’exploration en dehors de la classe – corrélation

R	R au carré	R au carré corrigé	Erreur de l’estimation standard	Corrélation de Pearson	Sig. (unilatéral)	N
.316	.100	.075	.4138	.316	.027	38

Les coefficients du modèle de régression sont les suivants:

Age de l’enseignant et activités d’exploration en dehors de la classe – modèle de régression

	Coefficients		Coefficients standard	t	Sig.	Corrélations
	B	Erreur standard	Beta			d’ordre zéro
(Constante)	.706	.268		2.639	.012
Age	.013	.006	.316	1.999	.053	.316
Variable dépendante: COP2 Fréquence des activités d’exploration en dehors de la classe

Nous pouvons donc exprimer le modèle qui explique les activités d’exploration en dehors de la classe avec l'age avec l'équation suivante:

Activités_exploration = .705 + 0.013 * AGE

Voici un nuage de points pour cette relation:

Modèle de régression linéaire. Est-que l'age peut expliquer les sorties ?

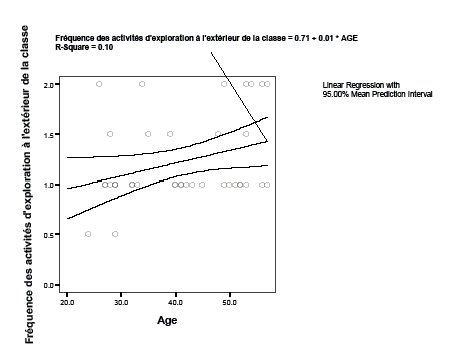
En regardant ce graphique, on s’aperçoit que que la relation est plutôt faible (autrement dit, ce graphisme montre pourquoi la corrélation est faible).

Le formule de régression peut être utilisée pour faire des prédictions précises, par exemple: «Un résultat de 2 sorties est prédit pour les gens de 100 ans».

.705 + 0.013 * 100 = 2.005

Régression multiple multivariée

Il arrive que l'on souhaite prédire l'effet de plusieurs VI (multiple) sur plusieurs VD (multivariée). On pourrait lancer des analyses de régression indépendantes pour chacune des VD, mais cela diminue la force statistique des analyses. Aussi vaut-il mieux réaliser dans ce cas une analyse de régression multiple multivariée.

Par exemple, nous souhaitons répondre à la question: quelles habiletés de lecture prédisent la rétention et la compréhension d'un document?

• Variables indépendantes : rétention et compréhension
• Variables dépendantes : vocabulaire, fluence, littératie

Comment faire avec SPSS

NB : Avant de lancer une régression multivariée, lancer une analyse de corrélation. Seules les VD qui corrèlent avec la/les VI seront inclues dans le modèle de régression.

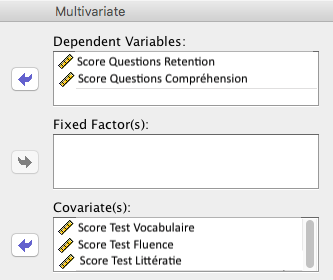
Sous SPSS une régression multivariée (multiple ou simple) est effectuée en utilisant la commande GLM-Multivariate:

• Lancer une première analyse
  • Insérer toutes les VD comme Dependent Variables.
  • Insérer toutes les VI comme Covariate(s).
  • Dans les Options : cocher les Parameters estimates pour obtenir les valeurs B pour chaque VD.
  • Ne rien mettre comme Fixed Factors.
  • Output : Les test univariés sont l'équivalent de régressions multiples séparées.
• Lancer une deuxième analyse pour obtenir les valeurs beta
  • Relancer la même analyse mais utiliser les valeurs standardisées de vos VD.
  • Output : Les valeurs des B de cette 2ème analyse sont vos beta.

source

Mesure d'estimation : Déterminer le modèle de régression le plus approprié

Qu'il s'agisse d'analyses de régression exploratoires (construction d'un modèle) ou d'analyse visant à déterminer lequel de deux modèles construit à partir de la théorie est le plus approprié, il faut savoir que comparer.

D'après Fields (2013, 4e édition), le problème de R² est que plus on entre de prédicteurs, plus la valeur du R² augmente. Il recommande donc d'utiliser plutôt le critère d'information d'Akaike (AIC). En lui même l'AIC ne signifie rien, mais c'est le modèle de régression avec le plus faible AIC qui est considéré comme le plus approprié.

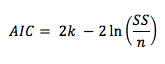
En cas d'analyse de régression avec un échantillon faible (n ± 40), préférez l'AICc.

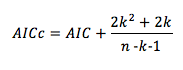
Liens

• Analyse de régression avec SPSS (montre comment créer un graphique)
• Procédure pour une régression multiple multivariée sous R