Introduction à la modélisation des données avec R

Cet article est en construction: un auteur est en train de le modifier.

En principe, le ou les auteurs en question devraient bientôt présenter une meilleure version.

---

Introduction

Étant R un logiciel utilisé très souvent dans le contexte du Data Science, il existe des nombreuses possibilités pour modéliser des données, notamment à travers une grande variété de paquets externes. La modélisation des données est un sujet très vaste et qui incorpore différentes approches philosophiques, théoriques et pratiques. Certaines sont déjà utilisées depuis longtemps en sciences sociales, comme les statistiques inférentielles de type fréquentiste, tandis que d'autres commencent à apparaître (e.g. statistiques Bayésiennes, machine learning), en dépit du fait qu'elles existent déjà depuis plusieurs années (voir siècles pour les statistiques Bayésiennes). Le point de contact parmi ses différentes approches est souvent identifié comme la séparation entre le signal et le bruit. Même si cette définition est probablement trop abstraite pour qu'elle puisse être utile sans une expérience préalable dans le domaine, elle permet d'éviter de tomber dans un champ plutôt qu'un autre. D'autres définitions qu'on peut parfois lire dans des livres de textes en sciences sociales (e.g. la réduction des données à un indicateur statistique ou encore la quantification de l'incertitude) ne sont souvent valables que dans une approche spécifique.

Dans cette page, nous proposons d'abord une description du fonctionnement technique de la modélisation en R, notamment en référence aux caractéristiques de Input et Output des fonctions qui s'occupent de modéliser des données. Deuxièmement, nous proposons un bref aperçu des débats et perspectives différentes concernant l'utilisation de la modélisation des données en sciences sociales. Ensuite, nous illustrons différents approches à la modélisation des données, avec une liste de paquets externes souvent utilisés dans l'approche de référence.

Prérequis

Cet article présuppose deux types de connaissances préalables :

• Techniques, relatives à l'utilisation de R
• Théoriques, relatives à des connaissances en modélisation des données

Connaissances techniques

Cette page fait partie du parcours guide Pensée computationnelle avec R et nécessitent pourtant au moins une première exposition à l'environnement de R et à la programmation. Si vous n'avez pas suivi le parcours guidé et vous avez une expérience limité avec R ou la programmation en général, la lecture de ces pages peut être utile :

• Introduction à la programmation

• Introduction conceptuelle à R

De plus, même si les exemples proposés dans la page peuvent être reproduit dans tout environnement qui supporte R, l'utilisation de RStudio est conseillée, voir à ce propos :

• Mise en place d'un environnement de travail avec R

Connaissances théoriques

Cet article aborde des concepts statistiques qui nécessitent au moins une expérience de base au préalable avec l'analyse de données quantitatives. Si vous avez suivi un cours en méthodologie de recherche en général ou en statistiques en particulier et mené une analyse statistique (e.g. régression linéaire, t-test, ANOVA, ...), vous pouvez suivre le contenu, même si très probablement certains informations seront nouvelles.

Si vous n'avez pas d'expérience au préalable ou vous préférez revoir certains principes avant d'aborder le contenu de cette page, vous pouvez vous référez au Manuel de recherche en technologie éducative, notamment aux sections consacrées aux données et analyses quantitatives :

• Statistiques descriptives et échelles
• Analyse de données quantitatives

Les informations du manuel sont largement généralisables à tout contexte en sciences sociales, même en dehors de la technologie éducative.

• Manuel de recherche en technologie éducative

Pensée computationnelle avec R

Cette page fait partie d'une collection de ressources visant l'introduction de principes computationnels en sciences sociales avec R. Voir :

• Pensée computationnelle avec R
• Pensée computationnelle en sciences sociales

Principes techniques de la modélisation des données

La modélisation des données en R, sauf quelques exceptions, suit toujours le même schéma de base dans lequel les données représentent l'Input et le modèle représente l'Output. Entre les deux, une fonction compute le modèle selon une formule (avec éventuellement d'autres paramètres) et le met à disposition, normalement avec des informations corollaires qui permettent, par exemple, d'évaluer sa pertinence ou de le visualiser graphiquement.

DONNÉES -> FONCTION(FORMULE, ....) -> MODÈLE

Modéliser à travers une formule

La plupart des paquets qui s'occupent de la modélisation des données en R utilise la même syntaxe, avec parfois quelques variations, pour expliciter les caractéristiques du modèle à utiliser, c'est-à-dire la relation entre les données/variables qui font partie du jeu des données. Voyons toute de suite un schéma essentiel qui sera ensuite adapté à des fonctions existantes :

# Exemple de la structure d'une fonction de modélisation (CODE NON EXECUTABLE)

my_model <- my_modeling_function(
  formula = y ~ x + z, 
  data = my_data, 
  [other_parameters, ...]
)

Analysons ce code en détail. La ligne 3 consiste dans une simple association entre une référence symbolique, my_model, avec le résultat de l'exécution d'une fonction de modélisation, my_modeling_function(). Bien entendu, il existe une différence substantielle entre ces deux composantes :

• La référence symbolique my_model peut avoir tout nom arbitraire que vous souhaitez utiliser, du moment qu'il respecte les règles syntaxique du langage
• La fonction de modélisation, nommée ici my_modeling_function(...), doit en revanche être une fonction existante, c'est-à-dire qu'elle est disponible dans l'environnement de la session de travail. Elle peut être à disposition de l'environnement de deux manières différentes :
  • Une fonction de modélisation déjà disponibles dans les paquets de R de base, comme par exemple lm() ou t.test()
  • Une fonction chargée à travers un paquet externe qui la met à disposition dans l'environnement, comme par exemple les paquets car ou afex

La ligne 4 introduit le concept fondamental de formule. La formule s'occupe de formaliser, avec une syntaxe concise, la relation entre les données/variables du modèle. Dans le cas de notre exemple, la formule se lit de la manière suivante :

y ~ x + z

• y représente la valeur que le modèle veut expliquer ou prédire. Selon l'approche utilisée à la modélisation, elle est souvent appelée variable dépendante (VD), variable expliquée, outcome ou explandandum
• Le symbole ~ (à lire tilde) peut se traduire avec la locution est expliqué/prédit par. Il sert donc à séparer la formule entre ce que nous souhaitons expliquer ou prédire, et les éléments utilisés pour effectuer l'explication ou la prédiction. Nous pouvons donc lire notre formule de la manière suivante y est expliqué/prédit par x et z.
• x et z sont par conséquent les valeurs qui expliquent ou prédisent y. Encore une fois, selon l'approche adoptée, on les identifie souvent en tant que variables indépendantes (VIs), prédicteurs, covariés, ou explanans

y, x et z font références à des valeurs contenus dans la structure de données qui est passée en argument à la ligne 5, avec le code data = my_data. Par conséquent, my_data doit être une structure de données qui peut identifier des valeurs y, x et z (pas forcément dans cet ordre). Dans la plupart de cas, il s'agit des noms des colonnes d'une structure de données de type rectangulaire (e.g. un data.frame dans R de base ou un tibble dans l'écosystème tidyverse) :

x	y	z	...
x1	y1	z1	...
x2	y2	z2	...
...	...	...	...
xn	yn	zn	...

À la ligne 6, la notation conventionnelle [other_parameters, ...] signale que certains fonctions de modélisation acceptent des paramètres supplémentaires qui permettent de mieux adapter la modélisation aux besoins particulier de l'analyse. Ces paramètres dépendent évidemment de la fonction spécifique utilisée et il est souvent nécessaire de consulter la documentation ou des tutoriels pour connaître les différentes possibilités. Si vous utilisez RStudio, il est également possible de se servir de la touche TAB à l'intérieur des parenthèses de la fonction pour avoir un aperçu des paramètres acceptés, souvent avec une explication qui peut déjà aider un peu :

Liste des paramètres d'une fonction de modélisation, lm() dans l'exemple

Différentes combinaisons dans la formule

La notation de la formule passée à la fonction doit évidemment s'adapter selon la modélisation à effectuer. On peut en effet combiner les éléments de différentes manières, en utilisant également d'autres symboles pour dénoter des rapports entre les éléments de la formule. Voici quelques exemples de notations qui sont valables dans plusieurs fonctions de modélisation, même dans des paquets externes. Pour brévité, nous utiliserons les termes de variable dépendante ~ variable(s) indépendante(s), abrégées en VD ~ VI, mais bien évidemment ces termes peuvent être substitués avec des combinaisons alternatives (e.g., outcome ~ prédicteur(s), explenandum ~ explenans, ...). Pour l'instant nous nous limitons à afficher la syntaxe avec une référence au nom de tests classiques, souvent utilisés en sciences sociales, qui peuvent être rapportés à la formule. Des exemples concrets plus bas illustrerons les conséquences sur le modèle.

• y ~ x

  La VD est expliquée par une seule VI (e.g. t-test, One-way ANOVA, régression linéaire simple)

• y ~ x + z + c + d

  La VD est expliquée par les 4 VIs (e.g., régression linéaire multiple)

• y ~ x + z + x:z

  La VD est expliquée par les 2 VIs, plus un effet d'interaction/modération, dénoté par x:z (e.g. ANOVA factorielle)

• y ~ x * z

  Même résultat du point précédent, mais en format raccourcis. L'utilisation de * implique automatiquement l'effet d'interaction/modération.

• y ~ .

  Raccourcis pour dénoter que la VD est expliquée par toutes les VIs de la structure de données (i.e. toutes les autres colonnes)

• y ~ . - w

  Raccourcis pour dénoter que la VD est expliquée par toutes les VIs de la structure de données (i.e. toutes les autres colonnes) sauf la VI w.

Version courte de la fonction de modélisation

Comme il arrive souvent en R, les noms des paramètres utilisés très souvent dans une fonction peuvent ne pas être explicités, à condition d'en respecter l'ordre. Par conséquent, plusieurs fonctions de modélisation peuvent se passer des noms des paramètres formula = ... et data = .... Par exemple :

my_model <- my_modeling_function(y ~ x + z, my_data)

Le Output d'une fonction de modélisation

Contrairement aux logiciels d'analyse statistiques de type point-and-click (SPSS, Jamovi, ...) qui affichent souvent un grand nombre de résultats suite à une analyse (mais parfois pas ceux qui nous intéressent vraiment...), le Output d'une fonction de modélisation avec R est simplement un objet, souvent de type liste, avec lequel on peut interagir ultérieurement, surtout si nous l'avons stocké dans une référence symbolique.

En revanche, s'il existe plus ou moins une certaine cohérence dans les formats d'Input des fonctions de modélisation (i.e. formula + data + autres paramètres), le format de Output peut varier énormément d'une fonction à l'autre, ce qui est souvent source de frustration et incompréhension. Nous verrons dans la suite de cet article que cet aspect peut être géré par des paquets externes qui s'occupent de mettre en forme les résultats des fonctions de modélisations, mais pour l'instant focalisons nous sur un exemple de Output.

Dans le code suivant, nous simulons le score de 200 participants au jeu Super Mario Bros. Le score est généré aléatoirement selon une distribution normale avec la moyenne de 100 et l'écart type de 15. Chaque joueur a utilisé soit le personnage Mario, soit le personnage Luigi. Ensuite, nous utilisons deux fonctions de modélisation disponibles out of the box en R qui nous permettrons de comparer les différences dans l'Output :

• la fonction lm(), qui correspond à une régression linéaire simple dans notre cas
• la fonction t.test() avec homogénéité de la variance, qui correspond à un test t de Student

Les deux modélisations sont attribuées respectivement aux références symboliques lm_model et t_model.

# Simulation de 200 scores M = 100, SD = 15, associés aléatoirement à deux personnages
game_scores <- data.frame(
  score = rnorm(200, 100, 15),
  player = sample(c("Mario", "Luigi"), 200, replace = TRUE)
)

# Régression linéaire simple
lm_model <- lm(
  formula = score ~ player, 
  data = game_scores
)

# Student t-test (homogénéité de la variance)
t_model <- t.test(
  formula = score ~ player, 
  data = game_scores, 
  var.equal = TRUE
)

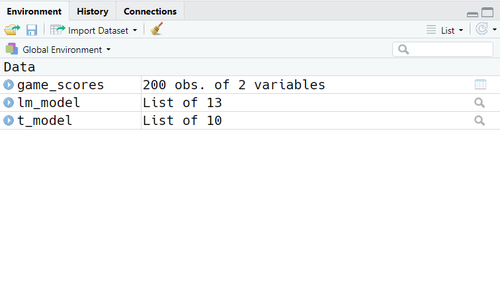
Lorsqu'on exécute ce bout de code, il n'y a aucun Output qui s'affiche à la console. En revanche, l'environnement global de votre session de travail se sera peuplé avec trois nouveaux éléments. Si vous utilisez RStudio, vous pouvez les noter dans le tab correspondant :

Deux fonctions de modélisations qui génèrent deux listes différentes

Nous pouvons noter que les deux Output des fonctions de modélisations sont deux listes, mais qu'elles diffèrent déjà dans le nombre d'éléments :

• lm_model est une liste avec 13 éléments
• t_model est une liste avec 10 éléments

Il existe différents possibilités pour interagir avec ce type d'Output, par exemple :

• Accès direct à l'Output général
• Accès aux sous-éléments de l'Output
• Passer le Output en tant que Input pour une autre fonction

Accès direct à l'Output général

On peut accéder à l'Output général si on saisie tout simplement la référence symbolique à laquelle nous avons associé le résultat de la fonction de modélisation (ou alternativement si on invoque directement la fonction sans passer à travers une référence symbolique). Cet Output général est une sorte de résumé que les créateurs de la fonction décident de mettre à disposition comme représentatif du modèle, mais qui n'est pas le seule résultat accessible. Voyons cette explication plutôt abstraite appliquée aux deux fonctions de modélisations que nous avons utilisées. Si on saisie respectivement les deux références symboliques des modèles, nous obtenons à la console deux messages très différents :

• lm_model

  Call:
  lm(formula = score ~ player, data = game_scores)
  
  Coefficients:
  (Intercept)  playerMario  
        99.77         2.84
  

• t_model

  Two Sample t-test
  
  data:  score by player
  t = -1.28, df = 198, p-value = 0.2
  alternative hypothesis: true difference in means is not equal to 0
  95 percent confidence interval:
   -7.2272  1.5508
  sample estimates:
  mean in group Luigi mean in group Mario 
               99.766             102.604
  

Le Output de t_model est beaucoup plus informatif par rapport à lm_model, avec déjà plusieurs indicateurs corollaires (e.g. le test statistique t, les degrés de liberté, la p-valeur, ...). En revanche, les informations affichées à l'écran ne représentent pas l'ensemble des informations qui sont disponibles avec le modèle. Nous verrons dans les deux sections suivantes comment extraire plus d'informations depuis le Output de la modélisation.

Accès aux sous-éléments de l'Output

Les sous-éléments de l'Output de la fonction lm()

Sous-éléments de la fonction de modélisation t.test()

Les résultats d'une fonction de modélisation sont des objets de R comme tous les autres. Il est donc possible d'accéder aux différents sous-éléments qui peuvent souvent donner des informations plus spécifiques. De plus, ces éléments peuvent être ré-utilisés dans d'autres computations, ou référencés dans la création dynamique de report (voir Introduction à Rmarkdown).

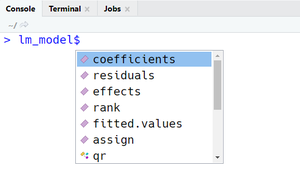
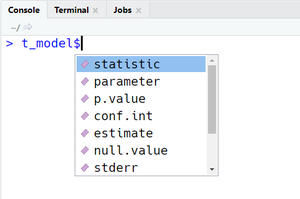
Dans nos exemples, il suffit d'ajouter le symbole $ de sélection d'un sous-élément dans une liste pour pouvoir accéder à des indicateurs des deux modèles. Si vous utilisez RStudio, la liste de sous-éléments va s'afficher à l'écran pour vous faciliter la tâche (voir Figures à côté). En alternative, on peut utiliser la fonction attributes() pour afficher à la console tous les sous-éléments et des informations complémentaires sur l'Ouput, comme par exemple sa classe :

• attribues(lm_model)

  $names
   [1] "coefficients"  "residuals"     "effects"       "rank"          "fitted.values"
   [6] "assign"        "qr"            "df.residual"   "contrasts"     "xlevels"      
  [11] "call"          "terms"         "model"        
  
  $class
  [1] "lm"
  

• attributes(t_model)

  $names
   [1] "statistic"   "parameter"   "p.value"     "conf.int"    "estimate"    "null.value" 
   [7] "stderr"      "alternative" "method"      "data.name"  
  
  $class
  [1] "htest"
  

Les sous-éléments peuvent être à leur tours des structures de données, par exemple des listes ou des vecteurs, et peuvent ainsi être ultérieurement sélectionnés de manière plus précise. Par exemple, on peut accéder singulièrement aux intervalles de confiances autour du t.test() de la manière suivante :

• Limit inférieur : t_model$conf.int[1]
• Limit supérieur : t_model$conf.int[2]

Passer le Output en tant que Input pour une autre fonction

L'Output d'une fonction de modélisation peut être passé en tant que Input à une autre fonction, qui s'occupe d'extraire différents indicateurs et les combiner. Par exemple, si on passe la référence symbolique à l'intérieur de la fonction summary() qui est souvent utilisée pour récupérer des informations depuis des structures de données ou listes, la situation par rapport à l'accès directe qu'on a vu plus haut est radicalement opposée :

• summary(lm_model)

  Call:
  lm(formula = score ~ player, data = game_scores)
  
  Residuals:
     Min     1Q Median     3Q    Max 
  -43.98 -11.44  -0.79  11.24  42.86 
  
  Coefficients:
              Estimate Std. Error t value            Pr(>|t|)
  (Intercept)    99.77       1.64   61.00 <0.0000000000000002
  playerMario     2.84       2.23    1.28                 0.2
  
  Residual standard error: 15.7 on 198 degrees of freedom
  Multiple R-squared:  0.00815,	Adjusted R-squared:  0.00314 
  F-statistic: 1.63 on 1 and 198 DF,  p-value: 0.204
  

• summary(t_test)

  Length Class  Mode     
  statistic   1      -none- numeric  
  parameter   1      -none- numeric  
  p.value     1      -none- numeric  
  conf.int    2      -none- numeric  
  estimate    2      -none- numeric  
  null.value  1      -none- numeric  
  stderr      1      -none- numeric  
  alternative 1      -none- character
  method      1      -none- character
  data.name   1      -none- character
  

Veuillez noter que la fonction summary() créé à son tour une liste d'éléments, que vous pouvez d'ailleurs associer à une autre référence symbolique à fin de récupérer un ou plusieurs indicateurs d'intérêt :

summary_lm_model <- summary(lm_model)

# Récupérer la taille de l'effet R-squared
summary_lm_model$r.squared

Un autre exemple concerne la fonction plot() (voir Introduction à la visualization des données avec R), dont le comportement est encore plus différent selon le modèle que vous passez en argument :

• plot(lm_model)

  Cette utilisation de la fonction crée 4 graphiques qui sont souvent utilisés pour évaluer les postulats d'une regression linéaire, car elle est pré-programmée pour traiter un objet avec la classe lm.

• plot(t_model)

  Cette utilisation de la fonction déclenche une erreur car elle n'est pas pré-programmée pour traiter un objet avec la classe htest.

Le comportement en terme de Input/Output d'une fonction qui s'occupe à son tour des résultats d'une fonction de modélisation peut donc varier selon les intentions des créateurs de la fonction. Avec le temps ou selon les contextes, des nouveaux indicateurs peuvent être intéressants ou nécessaires. Pour cette raison, il existe des paquets externes qui peuvent être plus adaptés aux besoins, comme par exemple le paquet broom illustré dans l'exemple suivant :

library(broom)

# Jeu de données alétaoires avec une VD, une VI catégorielle et une VI continue
sim_data <- data.frame(
  vd = rnorm(100),
  vi_cat = sample(c("Contrôle", "Traitement"), 100, replace = TRUE),
  vi_cont = runif(100)
)

# Modèle avec interaction
lm.model <- lm(vd ~ vi_cat + vi_cont + vi_cat * vi_cont, data = sim_data)

# Mettre en forme le paramètres du modèle
tidy(lm.model)

# Mettre en forme les observations par rapport au modèle
augment(lm.model)

# Résumé du modèle statistique
glance(lm.model)

Le paquet broom - qui fait partie de l'écosystème Tidyverse - met à disposition trois fonctions qui permettent de mieux accéder aux résultats d'un modèle statistique :

• tidy(model) permet de mettre en forme les différents paramètres du modèle. Dans le code d'exemple le résultat de la fonction tidy(lm.model) sera similaire à celui-ci :

  # A tibble: 4 x 5
    term                     estimate std.error statistic p.value
    <chr>                       <dbl>     <dbl>     <dbl>   <dbl>
  1 (Intercept)                0.0611     0.292    0.210    0.834
  2 vi_catTraitement          -0.303      0.424   -0.715    0.476
  3 vi_cont                    0.0248     0.488    0.0510   0.959
  4 vi_catTraitement:vi_cont   0.314      0.703    0.446    0.657
  

• augment(model) permet de confronter les observations par rapport au modèle. Dans le code d'exemple le résultat de la fonction augment(lm.model) sera similaire à celui-ci :

  # A tibble: 100 x 9
         vd vi_cat     vi_cont .fitted .resid .std.resid   .hat .sigma  .cooksd
      <dbl> <chr>        <dbl>   <dbl>  <dbl>      <dbl>  <dbl>  <dbl>    <dbl>
   1  2.65  Contrôle    0.373   0.0704  2.58       2.59  0.0233  0.977 0.0400  
   2  2.59  Traitement  0.196  -0.176   2.77       2.82  0.0511  0.970 0.107   
   3 -0.284 Contrôle    0.535   0.0744 -0.358     -0.359 0.0172  1.01  0.000565
   4  1.20  Traitement  0.536  -0.0608  1.26       1.27  0.0238  1.00  0.00979 
   5  0.835 Contrôle    0.639   0.0770  0.758      0.759 0.0199  1.01  0.00292 
   6 -0.677 Traitement  0.0374 -0.230  -0.447     -0.464 0.0839  1.01  0.00492 
   7 -1.22  Contrôle    0.274   0.0679 -1.29      -1.30  0.0329  1.00  0.0143  
   8  1.23  Contrôle    0.812   0.0813  1.15       1.16  0.0355  1.01  0.0124  
   9  0.825 Traitement  0.239  -0.161   0.987      1.00  0.0444  1.01  0.0117  
  10  1.22  Traitement  0.944   0.0772  1.14       1.17  0.0683  1.01  0.0252  
  # ... with 90 more rows
  

• glance(model) permet de résumer le modèle avec des indicateurs souvent utilisés dans les contributions scientifiques. Dans le code d'exemple le résultat de la fonction glance(lm.model) sera similaire à celui-ci :

  # A tibble: 1 x 12
    r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC deviance df.residual  nobs
        <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <int> <int>
  1   0.00942       -0.0215  1.01     0.304   0.822     3  -141.  291.  304.     97.5          96   100
  

Le paquet broom s'adapte à des modèles issues de différentes fonctions et paquets de modélisation. Dans tous les cas supportés, le Output des fonctions de broom sont des tibbles, c'est-à-dire une version avancée des data.frame de R et peuvent donc être utilisés pour récupérer les informations dans les lignes/colonnes (voir l'introduction à Tidyverse pour plus de détails).

Débats et perspectives dans la modélisation des données en sciences sociales

La modélisation des données est un sujet très vaste et complexe, qui implique plusieurs considérations philosophiques et méthodologiques qui dépassent le cadre introductif de cet article. Néanmoins, cette complexité se reflète inévitablement dans l'écosystème de R et il est donc utile de pouvoir l'aborder, au moins de manière superficielle.

Nous pouvons diviser les différences entre modélisations de données en deux grandes catégories :

1. Différences philosophiques et méthodologiques relatives souvent à des interprétations du concept de probabilité différentes;
2. Différences techniques au sein de la même approche philosophique/méthodologique dans l'implémentation pratique du même modèle.

Les deux catégories s'influencent mutuellement est sont destinées à changer dans le temps suite au débat et les indications de la communauté scientifique sur le sujet. En particulier dans ces dernières années, plusieurs propositions ont été faites pour modifier radicalement les pratiques dans l'analyse statistique dans les sciences sociales, notamment en psychologie. Nous proposons ici une liste non exhaustive de quelques propositions, en essayant de garder un regard neutre. L'utilité de cette liste est principalement celle de donner un aperçu de comment ces différences influencent profondément le fonctionnement, et par extension le choix, d'outils techniques de modélisation des données. Cette prémisse sert également à rendre attentif au fait que, parfois, la complexité de l'utilisation de R dans ce contexte relève principalement de la complexité du domaine lui-même. En d'autres termes, comparé à des logiciels de type point-and-click dans lequel les choix de l'utilisateur sont souvent forcées, en R il existe une plus grande flexibilité, accompagnée inévitablement par une plus grand choix d'options et par conséquent d'incertitude.

Ne plus utiliser le terme significatif dans l'interprétation d'un test statistique

L'utilisation du term significatif serait devenu désormais trop ambigu, surtout à cause d'une mauvaise compréhension de la p-valeur qui accompagne l'interprétation de la significativité statistique. Une confusion entre la significativité statistique et la significativité pratique serait l'une des conséquences majeure à la base de cette proposition. Par exemple, il peut arriver de lire dans un article scientifique qu'une différence entre moyennes significative à p=0.00001 est retenue comme plus importante d'un point de vue pratique qu'une différence à p=0.02. Ou encore que la significativité d'un indicateur statistique dont la p-valeur est comprises entre 0.05 et 0.1 soit considérée tendancielle. Vous pouvez retrouver cette approche dans les résultats des tests statistiques classiques (voir plus bas) en R avec l'utilisation d'astérisques qui accompagnent les paramètres. La présence de ces astérisques, qui peut-être gérée à travers une option, est ironiquement identifiée par certains avec la pratique du stargazing (regarder les étoiles). Voici un exemple basé sur un jeu de donné déjà disponible en R de base avec la référence mtcars. L'exemple en soit est inintéressant si ce n'est pour la forme de l'output :

# Stargazing is ON
options(show.signif.stars = TRUE)

# Regréssion linéaire multiple :
# consommation carburant (mpg) ~ puissance (hp) + poids (wt) + boîte de vitesse automatique/manuelle (am)
lm_cars <- lm(formula = mpg ~ hp + wt + am, data = mtcars)
summary(lm_cars)

Le Output du sommaire est le suivant :

Call:
lm(formula = mpg ~ hp + wt + am, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.422 -1.792 -0.379  1.225  5.532 

Coefficients:
            Estimate Std. Error t value         Pr(>|t|)    
(Intercept) 34.00288    2.64266   12.87 0.00000000000028 ***
hp          -0.03748    0.00961   -3.90          0.00055 ***
wt          -2.87858    0.90497   -3.18          0.00357 ** 
am           2.08371    1.37642    1.51          0.14127    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.54 on 28 degrees of freedom
Multiple R-squared:  0.84,	Adjusted R-squared:  0.823 
F-statistic:   49 on 3 and 28 DF,  p-value: 0.0000000000291

La ligne de l'Ouput Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1, ainsi que les différents astérisques à côté des paramètres de la régression linéaire multiple, illustrent bien cette approche. La présence de ces astérisques est donc déterminée par le rôle philosophique ou méthodologique qui est donnée à la p-valeur et au seuil de significativité (le niveau $\alpha$).

Utiliser les intervalles de confiance en plus (ou au lieu) de la p-valeur

Une autre proposition est celle d'intégrer, ou même remplacer, la p-valeur avec des intervalles de confiance construits autour du paramètre d'intérêt. On a déjà vue ces intervalles dans la modélisation avec la fonction t.test() plus haut dans la page. Le même Output est reporté ici :

Two Sample t-test

data:  score by player
t = -1.28, df = 198, p-value = 0.2
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -7.2272  1.5508
sample estimates:
mean in group Luigi mean in group Mario 
             99.766             102.604

Les intervalles de confiance à 95% dans cet Output sont construits autour de la différence observée dans les deux groupes (i.e. 99.766 - 102.604 = -2.838) et correspondent à :

• -7.2272 pour la limite inférieure
• 1.5508 pour la limite supérieure

Vu que l'écart entre les deux intervalles inclut 0, on ne peut pas rejeter l'hypothèse nulle (c'est-à-dire l'hypothèse qu'il n'y a pas de différence entre les deux moyennes), ce qui est corroboré d'ailleurs par la p-valeur=0.2 (en assumant un niveau alpha conventionnel de référence à 0.05). La proposition d'utiliser ces valeurs est liée à une interprétation plus simple de la précision du test statistique : un écart plus grand entre les deux intervalles correspond à une mineur précision comparé à un écart plus serré.

Cette approche philosophique et méthodologique implique, techniquement, aux fonctions de modélisation de calculer les intervalles de confiance autour des paramètres d'intérêt et, idéalement, de les mettre facilement à disposition pour pouvoir les reporter dans le résultat de l'analyse. La fonction t.test() le fait automatiquement, mais ce n'est pas le cas pour toutes les fonctions de modélisation.

Baser l'interprétation de résultats sur des indicateurs de magnitude (taille de l'effet)

Encore une autre proposition, liée d'ailleurs à la première sur l'abandon de l'utilisation du terme significatif en relation à la p-valeur, consiste à fonder toute discussion sur les implications d'un test statistique sur des indicateurs de magnitude, également appelée taille de l'effet. Il existe cependant différents indicateurs de la taille de l'effet, qui sont souvent regroupés en deux familles :

• La famille des indicateurs de type d, relatifs à la différence standardisée entre moyennes
• La famille des indicateurs de type r, relatifs à la force de l'association entre deux variables, souvent indiquée en terme de pourcentage de la variance expliquée par une ou plusieurs variables indépendantes/prédicteurs par rapport à la variable dépendante/outcome.

Les fonctions de modélisation en R peuvent par conséquent :

1. Ne pas fournir d'indications sur la taille de l'effet
2. Fournir des indicateurs de type d et/ou des indicateurs de type r
3. Fournir d'autres indicateurs encore, en alternative ou en plus des indicateurs de type d et/ou r

Par exemple, nous avons vu plus haut que le Output général de la fonction t.test() donnent plusieurs indicateurs, mais il n'y a aucune référence à la taille de l'effet. Pour la récupérer il faudra donc :

• La calculer en écrivant vous-mêmes le code pour implémenter la formule, par exemple, du d de Cohen (la différence entre les deux moyennes des groupes, divisés par l'écart type de l'échantillon total ou seulement du groupe contrôle)

  $d={\frac {{\bar {x}}_{1}-{\bar {x}}_{2}}{s}}={\frac {\mu _{1}-\mu _{2}}{s}}.$

• Utiliser un paquet de R qui le calcule pour vous, comme par exemple le paquet effectsize

Au contraire, le Output de la fonction summary() appliquée au résultat de la fonction lm() affiche directement la taille de l'effet de type R-squared et R-squared ajusté (lorsqu'il y a plusieurs variables indépendantes/prédicteurs).

La taille de l'effet est un indicateur qui est d'ailleurs utilisé également dans des paquets de R qui s'occupent de calculer la puissance statistique d'un test ou dans une méta-analyse (voir plus bas).

Paquets de R en relation avec la taille de l'effet :

• effectsize (Ben-Shachar, Makowski & Lüdecke, 2020)

Abandonner les tests statistiques basés sur l'hypothèse nulle

Enfin, une dernière proposition que nous reportons, plus radicale, consiste à abandonner complètement les tests statistiques basées sur l'hypothèse nulle (Null Hypothesis Significance Testing, NHST), c'est-à-dire l'approche philosophique et méthodologique dominant en sciences sociales depuis plusieurs décennies (voir statistiques fréquentistes plus bas). Les raisons apportées en support de cette proposition sont plusieurs et relèvent de différentes sources, comme par exemple :

• Philosophiques : ce type d'approche est étroitement lié à l'approche épistémologique hypothétique-déductive qui, selon certains, ne serait pas toujours adapté au contexte des sciences sociales ;
• Méthodologiques : les tests statistiques basées sur l'hypothèse nulle donnent une indication sur la probabilité d'obtenir des données similaires à celles obtenus dans l'échantillon si l'hypothèse nulle est vraie, ce qui se traduit en langage des probabilités P(D|H), à lire Probability of Data given the Hypothesis. Au contraire, les chercheurs sont plutôt intéressés à connaître la probabilité que l'hypothèse soit vraie en fonction des données, donc plutôt P(H|D), à lire Probability of the Hypothesis given the Data ;
• Pratiques : l'utilisation de NHST est souvent mal interprétée par les chercheurs, avec des erreurs méthodologiques et interprétatives qui remettent profondément en question la fiabilité des hypothèses (et par extension des théories) qui sont corroborées ou rejetées suite à un test statistique de ce type.

Les alternatives proposées à l'approche NHST sont en prévalence deux :

• Les statistiques Bayésiennes (voir plus bas)
• Les statistiques basées sur le concept de Likelihood

Des paquets de R proposent ainsi des test et fonctions de modélisation de données qui relèvent d'approches alternatives et qui peuvent donc nécessiter d'Input différents (e.g. pas de formule ou des formules différentes) et proposer des Output avec peu ou pas de lien avec les fonctions de modélisation classiques.

Différentes approches à la modélisation des données

Dans cette section, nous proposons un survol de différentes approches à la modélisation de données. Chaque approche inclut également une liste non exhaustive de paquets de R souvent utilisé dans ce contexte. La distinction entre approches essaie de suivre les différentes positions et techniques établies ou émergentes en sciences sociales dans les dernières années, mais ne vise surtout pas à renforcer des perspectives d'incommensurabilité entre approches. Au contraire, les techniques et finalités de la modélisation des données ont souvent des amples recouvrements.

Modélisation avec statistiques classiques ou fréquentistes

Les statistiques classiques ou fréquentistes représentent l'approche dominante aux statistiques en sciences sociales depuis plusieurs décennies. Dans l'interprétation la plus répandue de ce type d'approche, l'information est exclusivement contenue dans les données à disposition, à travers lesquelles les chercheurs essaient d'identifier la présence et la direction d'un effet (e.g., association ou relation causal). Pour ce faire, on utilise souvent le test basé sur l'hypothèse nulle, ou Null Hypothesis Significance Test (NHST) en anglais. Ce type de test, associé en général avec un seuil de significativité statistique $\alpha$, évalue la discrépance entre les données de l'échantillon et une distribution nulle qui représente une population dans laquelle il n'y a pas d'effet. Si la discrépance entre les données observées et la distribution nulle est suffisamment élevée, le seuil de significativité est franchi : la p-valuer observée est inférieur au seuil de significativité $\alpha$, souvent fixé à 0.05 de manière conventionnelle et arbitraire. À ce moment, l'hypothèse nulle est rejetée et la présence d'un effet est corroborée. La magnitude de cet effet est ensuite calculée à travers des indicateurs bruts (e.g. différence observée entre moyennes) ou standardisés (e.g. le R² ou le d de Cohen).

Dans cette section, nous proposons une liste non exhaustive de paquets souvent utilisés dans les statistiques classiques ou fréquentistes.

Paquet de base stats

Le paquet stats qui est disponible out of the box dans R propose plusieurs fonctions statistiques dans une perspective classique ou fréquentiste. Dans cette page, nous avons vu les fonctions lm() pour la régression linéaire et t.test() pour la comparaison entre deux moyennes. Il existe encore d'autres fonctions pour les statistiques fréquentistes les plus répandues au niveau paramétrique ou non-paramétrique. Ces fonctions sont en général plutôt vieilles, mais ne sont pas mises à jour pour éviter des problèmes de rétro-compatibilité, notamment car elles sont souvent utilisées par d'autres paquets qui sont des wrappers construits autour de ces fonctions de base.

Pour plus de détails, voir la page Analyses statistiques avec R.

Puissance statistique

Pour déterminer le nombre d'observations nécessaires afin d'évaluer la présence et direction d'un effet d'une certaine magnitude ou supérieur, on utilise de plus en plus des analyses de puissance statistique à priori, c'est-à-dire avant de recueillir des données. Ce type d'analyse permet de limiter l'erreur de Type II qui consiste à ne pas rejeter une hypothèse nulle, quand au contraire il faudrait la rejeter (e.g. dans une comparaison entre deux groupes, le test statistique ne franchit pas le seuil de significativité, lorsqu'en réalité les deux groupes sont différents).

Le paquet pwr (Champely, 2020) est souvent utilisé à cet effet. Par exemple, le code suivant détermine le nombre de participants nécessaires dans une comparaison bi-latérale entre deux groupes indépendants (i.e. un t-test) pour détecter un effet égale ou supérieur à d = 0.5 (i.e. moitié d'une écart type) avec un seuil de significativité (erreur de Type I) fixé à $\alpha =0.05$ et la puissance statistique (erreur de Type II) fixé à $1-\beta =0.9$ :

library(pwr)

pwr.t.test(
  d = 0.5, 
  sig.level = 0.05, 
  power = 0.9, 
  type ="two.sample", 
  alternative = "two.sided"
)

Le résultat de cette fonction montre qu'il faut environ 85 participants par groupe, donc 170 participants au total, pour pouvoir détecter une différence de d = 0.5 dans les deux groupes avec les valeurs $\alpha$ et $\beta$ choisi :

Two-sample t test power calculation 

              n = 85.03128
              d = 0.5
      sig.level = 0.05
          power = 0.9
    alternative = two.sided

NOTE: n is number in *each* group

Autres paquets utilisés pour les analyses de puissance statistique :

• Superpower (Caldwell,& Lakens, 2019) utilisé surtout pour des designs factoriels
• pwr2ppl (Aberson, 2020)

Régression linéaire

La régression linéaire est le type de modélisation le plus utilisé en sciences sociales : d'autres tests comme l'analyse de la variance (voir plus bas) sont des cas particuliers de la régression linéaire. Bien que R dispose de la fonction lm() pour ce type de modélisation, on utilise souvent également le paquet car (Fox & Weisberg, 2019) qui propose plusieurs fonctionnalités d'accompagnement à la modélisation basée sur la régression linéaire simple ou multiple, notamment en termes de visualisation. De plus, le paquet propose aussi des données (à travers le paquet carData importé automatiquement avec) qui peuvent être utilisées pour test ou exemple. Le code suivant utilise par exemple les données du jeu de données Salaries qui reporte le salaire de professeurs universitaires avec des prédicteurs comme le type de professeur-e (associate, full, ...), les années depuis le PhD, depuis le début du travail, et le sexe de la personne. Le jeu de données est utilisé dans l'exemple suivant, avec des fonctions du paquet car pour accompagner le modèle :

library(car)

model.salaries <- lm(salary ~ rank + yrs.since.phd + yrs.service + sex, data = Salaries)

# Summary
S(model.salaries)

#Residual plots
residualPlots(model.salaries)

#Outliers test
outlierTest(model.salaries)

#Added variables plots
avPlots(model.salaries)

#Leverage plot
leveragePlots(model.salaries)

Analyse de la variance

L'analyse de la variance (ANOVA) est un cas spécial de la régression linéaire (voir plus haut) souvent utilisé dans des designs expérimentaux où une ou plusieurs variables catégorielles (e.g. groupes expérimentaux) sont manipulées par les chercheurs. Bien que des analyses des variances puissent être menées avec la modélisation de la régression linéaire, il existe des paquets qui sont plus spécifiquement focalisés sur ce type d'analyse.

Le paquet afex (Singmann, Bolker, Westfall, Aust and Ben-Shachar, 2020), acronyme de Analysis of Factorial EXperiments, est un exemple de ce type de paquet. Il permet de spécifier des modélisations basées sur différents designs expérimentaux (one-way ANOVA, ANOVA factorielle avec ou sans interaction, ANOVA à mesure répétée). Il propose également la possibilité d'utiliser la modélisation linéaire multi-niveaux (Multi-Level Modeling).

Le code suivant montre une ANOVA factorielle avec deux facteurs (deux modalités chacun) et l'effet d'interaction sur des données simulées. À noter qu'il faut utiliser le format des données long (voir par exemple Introduction à Tidyverse). Le code utilise également le paquet emmeans (Lenth, 2020) pour des contrasts/comparaisons ultérieurs.

library(afex)
library(emmeans)

simulated_anova <- data.frame(
  participant_id = paste0("p", seq(1:400)),
  vd = rnorm(400, 100, 15),
  vi_1 = sample(c("Control group", "Treatment group"), 400, replace = TRUE),
  vi_2 = sample(c("Short training", "Long training"), 400, replace = TRUE)
)

#Modélisation avec indication du résidu avec Error(participant_id)
model.afex <- aov_car(vd ~ vi_1 * vi_2 + Error(participant_id), data = simulated_anova)

#Affichage avec la fonction "nice()"
nice(model.afex)

#Graphique
afex_plot(model.afex, "vi_1", "vi_2")

# Comparison avec le paquet emmeans
follow_up <- emmeans(model.afex, pairwise ~ vi_1 * vi_2)

La fonction nice(model.afex) affiche le résultat du test avec la colonne "ges" qui correspond au generalized effect size, une alternative à l'eta squared ou partial eta squared :

Anova Table (Type 3 tests)

Response: vd
     Effect     df    MSE      F  ges p.value
1      vi_1 1, 396 220.30   1.06 .003    .303
2      vi_2 1, 396 220.30   0.46 .001    .496
3 vi_1:vi_2 1, 396 220.30 3.04 + .008    .082
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘+’ 0.1 ‘ ’ 1

Modélisation avec statistiques Bayésiennes

Contrairement aux statistiques fréquentistes - qui sont déterminées exclusivement par les données observées - la modélisation avec les statistiques Bayésiennes utilise également des croyances qui sont définies à priori, et qu'on appelle par conséquent priors en anglais. Les priors sont des attentes que l'on peut avoir vis-à-vis de la distribution des données. Ces attentes peuvent représenter des connaissances dont nous disposons déjà sur le phénomène, ou une distribution hypothétique que les chercheurs postulent en relation avec leurs questions de recherche. Un modèle dans l'approche Bayésienne est donc calculé selon une formule qu'on peut synthétiser de la manière suivante :

modélisation = priors + données observées

Les statistiques Bayésiennes nécessitent d'une puissance computationnelle plus élevée par rapport aux statistiques fréquentistes. Cette nécessité est d'ailleurs l'une des raisons pour lesquelles elles sont moins répandues. Lors des dernières années, des techniques computationnelles puissantes et complexes, comme par exemple la technique Markov Chain Monte Carlo (MCMC), ont été rendues plus accessibles, ce qui permet de mener des analyses Bayésiennes sans avoir à utiliser des machines avec puissance de calcul inaccessible pour la plupart des chercheurs. Dans cette section, nous présentons brièvement deux paquets qui utilisent under the hood la plateforme de modélisation Stan.

Paquet rstanarm

Le paquet rstanarm ...

Voir aussi :

• rstanarm sur le site mc-stan.org

Paquet brms

Le paquet brms ...

Voir aussi :

• brms sur le site mc-stan.org

Machine Learning

Le machine learning, également appelé apprentissage automatique en français, est l'une des modélisation des données les plus célèbres en Data Science depuis quelques années. Son utilisation est en général associé à l'intelligence artificielle, mais la technique en soit peut être utilisée dans plusieurs domaines. Tandis que les statistiques inférentielles s'intéressent à établir la présence et la direction d'un effet dans une population, le machine learning s'intéresse davantage aux prédictions. Il existe principalement deux techniques de machine learning :

1. Supervised learning ou apprentissage supervisé en français

   Cette technique consiste à prédire un outcome spécifique qu'on ne connait pas, à partir de features (ou caractéristiques) connues. Pour ce faire, un algorithme est entraîné à travers un jeu de données dans lequel le outcome et les features sont disponibile, afin d'utiliser par la suite l'algorithme dans des situations où seulement les features sont connues. Par exemple, on peut utiliser un jeu de données avec les images de tableaux de différents peintres pour entraîner un algorithme à classer de nouveaux tableaux selon l'auteur correspondant.

2. Unsupervised learning ou apprentissage non-supervisé en français

   Cette technique consiste à extraire des régularités ou caractéristiques communes dans des données non étiquetées. En utilisant le même exemple, des images de tableaux sans le nom du peintre comme feature sont analysées et classées en groupes (ou clusters) en fonction de caractéristiques communes que l'algorithmes arrive à détecter (e.g. couleurs, formes, ...).

Supervised learning

Dans le cas de l'apprentissage supervisé, on utilise souvent une technique qui consiste à diviser un jeu de données en deux parties :

1. Une partie qui sert pour entraîner l'algorithme à prédire l'outcome sur la base des prédicteurs disponibles
2. Une partie qui sert ensuite pour tester la capacité de l'algorithme de prédire le outcome de données qui n'ont pas été utilisées pour entraîner l'algorithme

Il est en effet fondamentale que le test ne soit pas fait avec les mêmes données qui ont servi de base pour entraîner l'algorithme, car autrement la précision de l'algorithme serait gonflée simplement par le fait qu'il essaie de prédire des données qu'il connait déjà.

Voici un exemple avec des données simulées et qui utilise le paquet caret. L'algorithme essaie de prédire si une personne utilise un ordinateur Mac ou Windows (i.e. le outcome) sur la base de l'âge, l'expérience informatique perçue, le salaire et le nombre de dispositifs informatiques possédés :

library(caret)

simulated_data <- data.frame(
  outcome = sample(c("Mac", "Windows"), 500, replace = TRUE),
  age = round(runif(500, 18, 65)),
  perceived_it_exprience = round(rnorm(500, 100, 15)),
  salary = round(rnorm(500, 50000, 15000)),
  number_devices = sample(seq(1:5), 500, replace = TRUE)
)

# Séparer une partie pour l'entraînement (80% des données) et une pour le test (20% des données)
separation <- createDataPartition(
  simulated_data$outcome,
  p = 0.8,
  list = FALSE
)

# Créer les deux jeu des données training et test
training <- simulated_data[separation,] #Inclusion
test <- simulated_data[-separation,] #Exclusion

#Entraîner l'algorithme
trained_algorithme <- train(
  outcome ~ .,
  data = training,
  method = "glm",
  preProc = c("center", "scale")
)
trained_algorithme

# Utiliser l'algorithme pour prédire les données test
predicted_values <- predict(
  trained_algorithme,
  newdata = test
)
predicted_values

# Tester la prédiction comparé à l'outcome "réel"
accuracy <- sum(predicted_values == test$outcome) / length(predicted_values)
accuracy

En raison du fait que les données sont simulées aléatoirement, la précision de l'algorithme sera autour de 50% (avec quelques variations alétaroire), c'est-à-dire que l'algorithme n'est pas dans les conditions de prédire le outcome au-delà de la chance d'en prédire un sur deux comme en jetant une pièce.