« STIC:STIC III (2016)/Tables de multiplication » : différence entre les versions
m (→Réalisation) |
|||
| (16 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
par Sebastien Waeger | |||
= Introduction = | = Introduction = | ||
Le dispositif pédagogique décrit dans cette page, est destiné aux enfants de 7 à 8 ans. A cet age, les enfants scolarisés commencent à apprendre les multiplications, mais aussi les tables de multiplication. Dès lors, ces enfants devront être capables de comprendre les mécanismes qui composent l'opération de base qu'est la multiplication. | Le dispositif pédagogique décrit dans cette page, est destiné aux enfants de 7 à 8 ans. A cet age, les enfants scolarisés commencent à apprendre les multiplications, mais aussi les tables de multiplication. Dès lors, ces enfants devront être capables de comprendre les mécanismes qui composent l'opération de base qu'est la multiplication. | ||
| Ligne 47 : | Ligne 49 : | ||
'''Exemple d'utilisation :''' | '''Exemple d'utilisation :''' | ||
L'enfant mélange les jetons face cachée. Il pioche un premier jeton et le retourne afin de découvrir ce qui est gravé sur l'autre face. | L'enfant mélange les jetons face cachée. Il pioche un premier jeton et le retourne afin de découvrir ce qui est gravé sur l'autre face. L'enfant essaye alors de trouver quelle case de la grille correspond au résultat gravé sur le jeton. Il place alors le jeton sur la grille. Attention, il y a de fortes chance qu'un nombre se trouve à plusieurs endroit sur la grille. | ||
Une fois que la grille est pleine, l'exercice est terminé. Pour ajouter une dimension ludique à l'exercice, l'enfant peut se chronométrer pour une notion de scoring. | |||
== Pratique par le jeu à deux == | == Pratique par le jeu à deux == | ||
Pour utiliser le dispositif dans le but de s'entrainer à la multiplication, les enfants peuvent utiliser le dispositif ensemble sous la forme d'un jeu. | |||
Matériel utilisé : | |||
*Plateau avec la grille | |||
*Jetons face gravée | |||
'''Exemple d'utilisation :''' | |||
Les deux joueur se placent devant le plateau de jeu et séparent les jetons en deux partie. Chacun des joueurs a donc 77 jetons à sa disposition. Ils vont ensuite se donner un top départ et retourner le premier jeton afin de découvrir sa face gravée. Ils vont ensuite essayer de placer le jeton dans la grille, à l'intersection correspondant au résultat de la multiplication du nombre horizontale par le nombre verticale. La multiplication étant une opération commutative, un même nombre peut être représenté sur deux jetons ou plus. Lorsque le cas se présente, les joueurs ont la possibilité de se bloquer en posant le jeton à l'endroit ou il pense que l'autre joueur voudrai le mettre, afin que ce dernier doive trouver une nouvelle position. Le premier joueur à avoir déposé la totalité de ses jeton gagne la partie. | |||
= Fondements théoriques = | = Fondements théoriques = | ||
| Ligne 64 : | Ligne 78 : | ||
== Pédagogie Montessori == | == Pédagogie Montessori == | ||
(Article détaillé sur la [[Pédagogie Montessori]]) | (Article détaillé sur la [[Pédagogie Montessori]]) | ||
La [[Pédagogie Montessori]] laisse une place centrale à l'apprentissage sensoriel. Il est donc primordiale de fournir à l'apprenant un matériel palpable. Dans le cas de l'apprentissage des multiplication, l'apprenant peut déplacer les jetons et les toucher. Il peut appréhender ce nouveau concept en formant des séries et en constatant par lui même que lorsqu'il réalise avec ses jeton 4x3, c qu'il réalise en faite c'est 4 série de trois jetons. Il a alors la possibilité de les enlever de la grille et les compter un par un, afin d'arriver au résultat total. | |||
== Drill & Practice == | == Drill & Practice == | ||
Edward Thorndike, psychologue américain et précurseur du Behaviorisme, propose une méthode d’enseignement dans laquelle l’enseignant aménage des séquences d’apprentissage au sein desquelles, les connexions stimulus-réponse les plus simples sont présenté d'abord aux apprenant, pour ensuite terminer par les plus complexes. Par exemple, selon l’auteur, l’opération arithmétique 4+4=8 est plus facile que 31+25=53. | |||
En partie basé sur le Behaviorisme, les notions de répétition et de conditionnement ont une place importante dans la méthode du Drill & Practice. C'est par la répétition de ces multiplications, que l'apprenant sera en mesure en mesure de retenir les information. A force de calculer le fait que 2x3 est égale à 6, l'apprenant va, au bout d'un certain, développer un automatisme quant à cette opération. | |||
= Réalisation = | = Réalisation = | ||
| Ligne 93 : | Ligne 110 : | ||
Voici les temps de découpe et de gravure pour la réalisation du set complet : | Voici les temps de découpe et de gravure pour la réalisation du set complet : | ||
*Temps total : 70 min | |||
*Temps total : | |||
== Dessins == | |||
* [http://tecfaetu.unige.ch/etu-maltt/volt/waegers0/stic-3/Projet/ Dessins] ([http://creativecommons.org/licenses/by-nc/4.0/ Licence Creative Commons Attribution - Pas d’Utilisation Commerciale 4.0 International]) | |||
= Bibliographie = | = Bibliographie = | ||
*Montessori, M. (2013). The montessori method. Transaction publishers. | |||
*Crahay, M (1999). Psychologie de l'éducation, Paris, PUF. | |||
*[https://sylviedesclaibes.com/2014/08/18/3536/|Lycée International Montessori – Ecole Athéna – Le blog de Sylvie d'Esclaibes.] | |||
[[Catégorie: Découpe laser]] | |||
[[Catégorie: Jeux pédagogiques]] | |||
[[Category: Objet d'apprentissage tangible]] | |||
Dernière version du 2 mai 2017 à 18:36
par Sebastien Waeger
Introduction
Le dispositif pédagogique décrit dans cette page, est destiné aux enfants de 7 à 8 ans. A cet age, les enfants scolarisés commencent à apprendre les multiplications, mais aussi les tables de multiplication. Dès lors, ces enfants devront être capables de comprendre les mécanismes qui composent l'opération de base qu'est la multiplication.
Ce dispositif propose donc une méthode d'apprentissage en trois étapes, basées en partie sur les principes de la méthode d'éducation Montessori (Montessori, 2013). Dans cette pédagogie, l'apprentissage de l'enfant passe par un apprentissage sensoriel. Il utilise des objets, les touche, les manipule et développe son intelligence grâce à une perception tangible du matériel qui lui est fourni. Le support physique a donc une place centrale au sein de cette pédagogie. Un dispositif réalisé sur la découpe et gravure laser se prête donc parfaitement à ce type de méthode.
Matériel
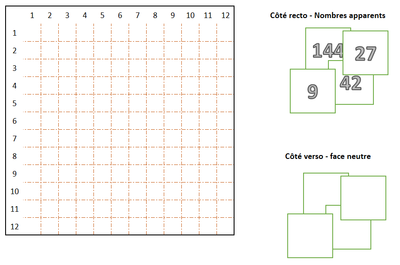
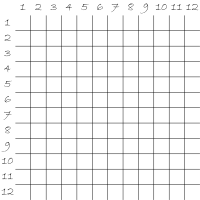
Le dispositif est composé d'un plateau, gravé d'une grille. Cette grille de 144 cases, représente les tables de multiplications des nombres de 1 à 12. Au dessus de cette grille, et sur son côté gauche, sont gravés les nombres de 1 à 12. Ces derniers représentent les intitulés de chacune des colonnes et lignes. L'intersection d'une colonne et d'une ligne représente donc la multiplication de leurs en-têtes respectives.
Le dispositif comprend aussi 144 jetons représentants les résultats de toutes les multiplications des tables de 1 à 12. Chacun de ces jeton à une des face gravée d'un nombre, tandis que l'autre face est vierge de toute inscription.
Utilisation
Il y a trois méthodes bien distinctes d'utilisation du dispositif. Chacune de ces méthode utilise le matériel à disposition d'une manière différente, ceci permettant d'accompagner l'enfant lors de son apprentissage de la multiplication.
Apprentissage des multiplications
Pour utiliser le dispositif dans le but d'apprendre les principes de la multiplication, cette méthode requiert la présence d'un tuteur ou d'un enseignant les premiers temps. Cela peut se faire avec un groupe d'enfant (4 ou 5 maximum) ou de manière individuelle.
Matériel utilisé :
- Plateau avec la grille
- Jetons face neutre
Le but de cette utilisation est d'apprendre à l'enfant les mécanismes de la multiplication. Pour ce faire, il faut se munir du matériel précédemment décrit. Il faut faire comprendre à l'enfant, que la multiplication consiste à mettre plusieurs fois le même nombre de jeton.
Exemple d'utilisation :
Il est d'abord proposé à l'enfant de réaliser la multiplication 2x5. Il faut donc guider l'enfant afin qu'il réalise 2 fois une rangée de 5 jetons. Une fois que l'enfant a déposé les jetons sur la grille, sous la forme de ces deux rangées, il lui est proposé de compter le nombre de jetons déposé. En comptant avec lui, le résultat trouvé sera 10 jetons. L'expérience peut être reproduite en réalisant la multiplication 5x3. L'enfant va déposer 5 rangées de 3 jetons chacune. A nouveau, le nombre total de jetons déposé sera compté, afin d'obtenir un total de 15.
Cette exercice doit être réalisé à de multiples reprises, jusqu'à ce que l'enfant soit en mesure de comprendre le mécanisme à la base de la multiplication. Chaque exercice peut être terminé par une phrase du type "5 multiplié par 3 égale à 15", afin de fixer les résultats obtenus.
Une fois que l'enfant à bien compris le principe, il peut essayer de résoudre des multiplications de manière indépendante.
Entrainement aux multiplications
Pour utiliser le dispositif dans le but de s'entrainer à la multiplication, l'enfant peut utiliser le dispositif de manière individuel.
Matériel utilisé :
- Plateau avec la grille
- Jetons face gravée
Le but de cette utilisation est d'entrainer la multiplication. L'enfant doit acquérir des réflexe quant aux résultat des tables de 1 à 12.
Exemple d'utilisation :
L'enfant mélange les jetons face cachée. Il pioche un premier jeton et le retourne afin de découvrir ce qui est gravé sur l'autre face. L'enfant essaye alors de trouver quelle case de la grille correspond au résultat gravé sur le jeton. Il place alors le jeton sur la grille. Attention, il y a de fortes chance qu'un nombre se trouve à plusieurs endroit sur la grille.
Une fois que la grille est pleine, l'exercice est terminé. Pour ajouter une dimension ludique à l'exercice, l'enfant peut se chronométrer pour une notion de scoring.
Pratique par le jeu à deux
Pour utiliser le dispositif dans le but de s'entrainer à la multiplication, les enfants peuvent utiliser le dispositif ensemble sous la forme d'un jeu.
Matériel utilisé :
- Plateau avec la grille
- Jetons face gravée
Exemple d'utilisation :
Les deux joueur se placent devant le plateau de jeu et séparent les jetons en deux partie. Chacun des joueurs a donc 77 jetons à sa disposition. Ils vont ensuite se donner un top départ et retourner le premier jeton afin de découvrir sa face gravée. Ils vont ensuite essayer de placer le jeton dans la grille, à l'intersection correspondant au résultat de la multiplication du nombre horizontale par le nombre verticale. La multiplication étant une opération commutative, un même nombre peut être représenté sur deux jetons ou plus. Lorsque le cas se présente, les joueurs ont la possibilité de se bloquer en posant le jeton à l'endroit ou il pense que l'autre joueur voudrai le mettre, afin que ce dernier doive trouver une nouvelle position. Le premier joueur à avoir déposé la totalité de ses jeton gagne la partie.
Fondements théoriques
Objectifs pédagogiques
L'utilisation de ce dispositif à 3 objectifs pédagogiques distincts :
Le premier objectif est l'apprentissage et compréhension des tables de multiplication selon la pédagogie Montessori. Cette apprentissage est réalisé lorsque le dispositif est utilisé comme décrit sous Apprentissage des multiplications.
Le second objectif est la pratique et l'entrainement des tables de multiplication. Cette pratique s'inscrit dans une pédagogie de Drill & Practice. L'utilisation du dispositif décrit dans la section Entrainement aux multiplications.
Enfin, le dernier objectif est la pratique ludique de la multiplication au travers du jeu à deux. Cette dernière se base sur les principes du Socio-constructivisme mais aussi du Drill & Practice. L'utilisation du dispositif comme décrit en section Pratique par le jeu à deux est propice à cet apprentissage.
Pédagogie Montessori
(Article détaillé sur la Pédagogie Montessori)
La Pédagogie Montessori laisse une place centrale à l'apprentissage sensoriel. Il est donc primordiale de fournir à l'apprenant un matériel palpable. Dans le cas de l'apprentissage des multiplication, l'apprenant peut déplacer les jetons et les toucher. Il peut appréhender ce nouveau concept en formant des séries et en constatant par lui même que lorsqu'il réalise avec ses jeton 4x3, c qu'il réalise en faite c'est 4 série de trois jetons. Il a alors la possibilité de les enlever de la grille et les compter un par un, afin d'arriver au résultat total.
Drill & Practice
Edward Thorndike, psychologue américain et précurseur du Behaviorisme, propose une méthode d’enseignement dans laquelle l’enseignant aménage des séquences d’apprentissage au sein desquelles, les connexions stimulus-réponse les plus simples sont présenté d'abord aux apprenant, pour ensuite terminer par les plus complexes. Par exemple, selon l’auteur, l’opération arithmétique 4+4=8 est plus facile que 31+25=53.
En partie basé sur le Behaviorisme, les notions de répétition et de conditionnement ont une place importante dans la méthode du Drill & Practice. C'est par la répétition de ces multiplications, que l'apprenant sera en mesure en mesure de retenir les information. A force de calculer le fait que 2x3 est égale à 6, l'apprenant va, au bout d'un certain, développer un automatisme quant à cette opération.
Réalisation
Matériel
La totalité du matériel a été réalisé avec le logiciel Inkscape, sous forme de fichier SVG.
La grille servant de plateau pour la dépose des pièces, est composé de 11 lignes verticales et 11 lignes horizontales. Ces dernières forment une grille de 144 cases représentant chacune le résultat d'une multiplication. Cette grille comporte les chiffres de 1 à 12 sur son bord supérieurs mais aussi sur son bord gauche. La police de caractère utilisé pour l'écriture des chiffre est Bradley Hand ITC. Chaque case de la grille fait 3cm x 3cm, tandis que le plateau en lui même a une dimension totale de 39cm x 39cm. Afin de rentrer dans les dimensions du plateau d'impression, cette image à été réduite à 78,2% de sa taille soit 30,5cm x 30,5cm.
Chaque jeton est composé d'un cercle de rayon de 1cm. Au centre de chaque cercle, un nombre est inscrit, représentant le résultat d'une multiplication. La police de caractère utilisée pour l'écriture de ces nombre est Lucida Handwriting. Afin de faciliter la découpe, les 144 jetons nécessaires à la réalisation du matériel ont été placés sur un seul fichier SVG.
De manière générale, les lignes avec une épaisseur inférieure à 0.01mm de couleur rouge seront découpées, tandis que les dessins plus épais de couleur noir seront gravés.
Découpeuse laser
Le matériel, réalisé dans le cadre de ce projet, a été découpé à l'aide d'une découpeuse laser Trotec Speedy 100R. La taille du plateau de découpe est de 61cm x 30.5cm avec une vitesse de découpe de 180 cm/s.
Les paramètres utilisés pour la découpe et la gravure sont les suivants :
- Puissance de découpe : 100
- Vitesse de découpe : 1
- Longueur d'onde découpe : 1000
- Puissance de gravure : 50
- Vitesse de gravure : 100
- Résolution de gravure : 500PPI
Voici les temps de découpe et de gravure pour la réalisation du set complet :
- Temps total : 70 min
Dessins
Bibliographie
- Montessori, M. (2013). The montessori method. Transaction publishers.
- Crahay, M (1999). Psychologie de l'éducation, Paris, PUF.
- International Montessori – Ecole Athéna – Le blog de Sylvie d'Esclaibes.