STIC:STIC III (2018)/TI-ssu

Physicalisation de données
Module: STIC:STIC III (2018)/Projets
⚐ à finaliser	☸ débutant
⚒ 2019/02/11

TI-ssu

Description

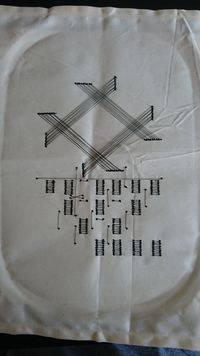
La TI-ssu (pour "Tecfa instrument sur tissu") est une broderie interactive qui peut calculer le produit de deux nombres compris entre 1 et 99 (usage unique).
L'interactivité se fait en défaisant la broderie. En enlevant des fils et en comptant le nombre d'intersections des fils restants, le résultat de la multiplication apparaît.

Origine

La TI-ssu a été développée par Léonard Truscello pendant le cours de STIC III de l'année 2018-2019
La méthode pour faire la multiplication est inspirée d'une représentation graphique de multiplication qui utilise des lignes. Voici une vidéo qui présente cette méthode.

Méthode de calcul

Partie supérieure

Description

Chaque bande de la partie supérieure a neuf lignes. Chaque bande croise deux autres bandes. Ces croisement créent quatre secteur d'intersections de forme carré. Ces quatre secteurs d'intersections sont répartis en trois parties :

• La partie de gauche avec un secteur d'intersections
• La partie du milieu avec deux secteurs d'intersections
• La partie de droite avec un secteur d'intersections

Calcul

Dans le calcul de deux nombres entre 1 et 99, chaque bande est associée à un nombre compris entre 0 et 9. L'association se fait en arrachant des fils de la bande et en laissant le nombre de fil correspondant à la bande. Un nombre est représenté entièrement par deux bandes parallèle. La dizaine est représentée par la bande la plus à gauche de la paire de bande parallèle et l'unité par la bande la plus à droite.
Par exemple, pour écrire 34 x 87 :

• la bande qui commence en haut à gauche du secteur d'intersection de la partie gauche sera composé de 3 fils.
• La bande parallèle à celle-ci aura 4 fils (i.e. la bande qui commence en haut à gauche du secteur d'intersection le plus haut)
• La bande parallèle qui commence en bas à droit du secteur d'intersection de la partie gauche sera composé de 8 fils.
• La bande parallèle à celle-ci aura 7 fils (i.e. la bande qui commence en bas à gauche du secteur d'intersection le plus bas)

S'il y a un zéro dans un des nombres, il faudra enlever tous les fils correspondant à la bande en question. Par exemple 7 x 12 sera calculé comme 07 X 12 et aura 0 fil dans la bande des dizaines parallèle à la bande 7.

Partie inférieure

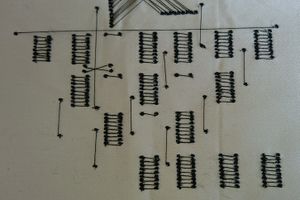
La partie inférieure permet d'inscrire les résultats de la partie supérieure. Il y a 4 niveaux horizontaux qui permettent de calculer le résultat de la multiplication. Les éléments composés de lignes horizontales correspondent à des nombres. Pour inscrire un nombre, il faut couper les lignes de manière à laisser le nombre souhaité. Par exemple pour obtenir 4, il faut laisser 4 lignes.
Les lignes verticales permettent de délimiter les différentes parties de chaque niveau. Les colonnes et les parties se comptent à partir de la droite. Une référence à la deuxième colonne signifie la deuxième colonne à partir de la droite.

Niveau 1

Le niveau 1 est séparé par des lignes verticales en 3 parties. Dans chaque partie, il faut inscrire le nombre d'intersection compté dans le ou les secteurs d'intersection correspondant.
La partie droite correspond au secteur d'intersection droit. Pour écrire 45, par exemple, il faut laisser 5 lignes dans la colonne tout à droite et 4 lignes dans l'avant dernière colonne. Les parties de droite et de gauche peuvent écrire des nombres allant de 0 à 89. La partie du milieu peut elle écrire des nombres de 0 à 199.

Niveau 2

Le niveau 2 est composé de 4 parties et de 5 colonnes.

• La première partie tout à droite est vierge, il n'y a pas de colonne.
• La deuxième partie est le résultat de l'addition de la deuxième et troisième colonne du niveau 1. La somme peut aller de 0 à 19.
• La troisième partie est le résultat de l'addition de la quatrième et sixième colonne. La somme peut aller de 0 à 19. Les lignes croisées entre le niveau 1 et 2 sont là pour indiquer dans quelle partie la cinquième colonne et sixième colonne du niveau 1 seront comptées.
• La quatrième partie est le résultat de l'addition de la cinquième colonne et de la septième colonne du niveau 1. La somme peut aller de 0 à 9. Les lignes croisées entre le niveau 1 et 2 sont là pour indiquer dans quelle partie la cinquième colonne et sixième colonne du niveau 1 seront comptées.

Niveau 3

Le niveau 3 est composé de 3 parties et de 3 colonnes.

• La première partie à droite est vierge, il n'y a pas de colonne.
• La deuxième partie est le résultat de l'addition de la deuxième et troisième colonne du niveau 2. La somme peut aller de 0 à 19.
• La troisième partie est le résultat de l'addition de la quatrième et cinquième colonne du niveau 2. La somme peut aller de 0 à 9.

Niveau 4

Le niveau 4 est le résultat de la multiplication. Le résultat se lit de gauche à droite comme un nombre normal. Il est compris entre 0 et 9'999.

• Le nombre de la colonne 1 est le même que celui de la colonne 1 du niveau 1.
• Le nombre de la colonne 2 est le même que celui de la colonne 1 du niveau 2.
• Le nombre de la colonne 3 est le même que celui de la colonne 1 du niveau 3.
• Le nombre de la colonne 4 est le résultat de l'addition de la deuxième et troisième colonne du niveau 3.

Usage pédagogique

Bien que cette broderie a été créée, en premier lieu, pour visualiser une manière d'utiliser la technique de défaire des fils pour interagir avec une broderie, un usage pédagogique est envisageable. La multiplication en colonne enseignée en primaire est une étape délicate pour l'élève et l'enseignant. La représentation graphique avec l'usage de ligne permet d'amener une autre manière d'appréhender la multiplication pour les élèves ayant des difficultés avec la multiplication. Utiliser la TI-ssu pour une première approche de la multiplication amènerait un élément tangible et manuel dans l'apprentissage de celle-ci.
Les mathématiques sont aussi souvent critiquées pour être genrées : "les garçons seraient meilleurs que les filles en math". La broderie étant elle aussi genrée et associée aux filles plutôt qu'au garçons, l'hypothèse serait que la TI-ssu permettrait de réduire l'impa ct genré de l'apprentissage des mathématiques et ici de la multiplication chez les filles. Bien évidemment l'hypothèse est à tester.

Développement

Il y a plusieurs manières de développer la TI-ssu, une idée serait de transformer les nombres en colonne de la partie inférieure en nombre digital. Le résultat serait visuellement plus explicite.
Pour avoir une TI-ssu terminée, il faut enlever manuellement environ 150 fils avant d'avoir le rendu présenté plus haut. En changeant de couleur, la brodeuse ne coudrait par les fils entre les points et diminuerait le traitement post-brodeuse.
En utilisant un tissu et un tambour plus grand, il serait possible de faire une multiplication entre deux nombres compris entre 0 et 999.