Introduction à la visualisation des données avec R
Cet article est en construction: un auteur est en train de le modifier.
En principe, le ou les auteurs en question devraient bientôt présenter une meilleure version.
| Pensée computationnelle avec R | |
|---|---|
| ⚐ à finaliser | ☸ débutant |
| ⚒ 2023/01/11 | |
| Catégorie: R | |
Introduction
L'une des utilisations les plus fréquentes de R concerne la création de visualisations des données à différents niveaux de complexité et pour différents objectifs. Notamment, on peut diviser les visualisations des données en deux grandes catégories :
- Visualisations exploratoires, dont la finalité consiste principalement à mieux comprendre des données ;
- Visualisations communicationnelles, dont la finalité est de synthétiser les résultats dans une forme graphique qui permet aux lecteurs de mieux les comprendre par rapport à des formes alternatives (e.g. texte ou tableau).
De plus, les deux types de visualisations peuvent être statiques ou dynamiques/interactives. Les représentations statiques sont les plus répandues dans les contributions scientifiques. Néanmoins, certains visualisations plus complexes peuvent bénéficier d'interactivité, comme par exemple la possibilité de zoomer sur une partie du graphique, mettre en évidence une observation spécifique parmi toutes les observations affichés, etc.
La flexibilité de R fait ainsi qu'on puisse utiliser les mêmes principes et outils pour les deux finalités et dans les deux modalités (statique ou interactive). De plus, les visualisations peuvent être intégrées directement dans un flux de travail plus large, incluant notamment la génération de report scientifiques (voir à ce propos Introduction à Rmarkdown) ou des pages web à publier.
Dans cet article nous proposons un introduction général à la visualisation des données à travers un langage de programmation, ce qui comporte une approche différente par rapport aux logiciels de type point-and-click. Nous utiliserons des exemples du paquet graphics qui est disponible par défaut en R afin de pouvoir tester les exemples rapidement, sans installer des paquets supplémentaires. En revanche, ce paquet est plus difficile à utiliser par rapport à des paquets externes plus récents et puissants, dont nous proposons une liste non exhaustive dans l'article.
Prérequis
Aucune connaissance préalable n'est nécessaire pour suivre le contenu de cet article. Cependant, pour maximiser sa compréhension et la possibilité d'appliquer directement les éléments traités, les articles suivants peuvent être très utils :
De plus, même si les exemples proposés dans la page peuvent être reproduit dans tout environnement qui supporte R, l'utilisation de RStudio est conseillée, voir à ce propos :
Générer des visualisations des données avec du code
Il existe plusieurs possibilités pour générer des visualisations des données, comme par exemple en utilisant un logiciel d'analyse statistique (e.g. SPSS ou Jamovi), un logiciel de type spreadsheet (e.g. Excel), ou encore un logiciel consacré précisément à cette démarche (e.g. Tableau Software). L'utilisation de R dans ce contexte présente les avantages en termes de flexibilité, adaptabilité et réutilisation du code. Dans cette section, nous aborderons brièvement cet aspect : comment générer des visualisations de données avec du code ? À titre d'exemple, nous utiliserons des fonctions du paquet graphics qui est disponible par défaut avec R. Les exemples disponibles dans cette section peuvent donc être testé directement, sans l'installation d'autres paquets supplémentaires.
Fonctions graphiques
Le principe est assez simple une fois qu'on comprend la logique plus étendue d'un langage de programmation (voir Introduction conceptuelle à R) : il existe des procédures (ou fonctions) qui transforment des données en représentations graphiques. Voyons tout de suite un exemple de base :
# Générer aléatoirement 100 chiffres entre 1 et 100
simulated_data <- sample(1:10, size = 100, replace = TRUE)
# Les afficher en histogramme
hist(simulated_data)
Ce code fait deux choses :
- À la ligne 2, nous créons 100 chiffres aléatoires entre 1 et 10 et nous les stockons avec la référence symbolique
simulated_data - À la ligne 5, nous utilisons la fonction
hist()en lui passant en argument nos données à travers la référence symbolique que nous venons de créer :hist(simulated_data)
Le résultat (qui s'affiche dans le tab Plot si vous utilisez RStudio) sera similaire à l'image suivante :
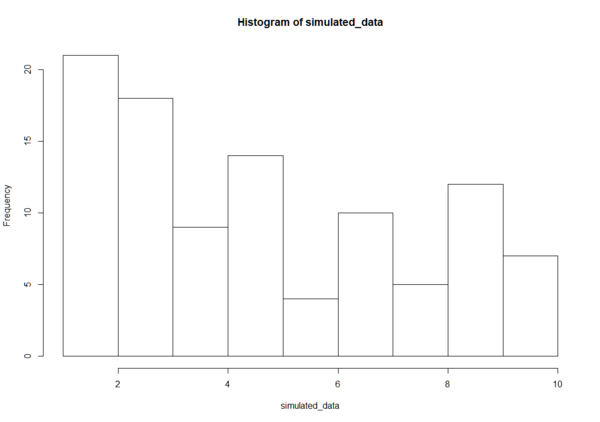
Utiliser des arguments pour adapter le graphique
Le principe de base vu dans le point précédent peut être complexifié en utilisant d'autres arguments dans la fonction qui permettent d'adapter le graphique selon les besoins :
# Adapter le graphique avec des arguments
hist(
simulated_data,
main = "Simulation de 100 données entre 1 et 10",
xlab = "Données simulées",
ylab = "Nombre d'occurence",
col = "lightblue",
)
La fonction hist() est la même, ainsi que son premier argument simulated_data. La fonction accepte également d'autres arguments, comme par exemple :
- Ligne 4
main = "Simulation de 100 données entre 1 et 10"modifie le titre du graphique - Lignes 5 et 6 modifient respectivement la labellisation des axes x et y
- Ligne 7
col = "lightblue"modifie la couleur des colonnes du histogramme
Le résultat sera similaire à l'image suivante :
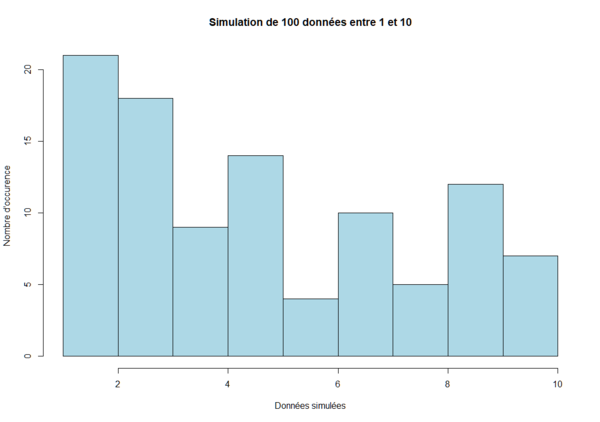
Complexification du principe de base
R permet de créer une énorme variété de représentations graphiques, du simple au très complexe, que ce soit à travers des fonctions disponibles dans les paquets de base ou à travers des paquets externes. Dans tous les cas, il s'agit d'une complexification de cet exemple de base. Dès que les visualisations deviennent plus complexes, la création du code devient également plus articulée, ce qui requiert un effort de mémorisation (ou une référence à portée de main) pour se rappeler des noms de fonctions et arguments nécessaires. Néanmoins, cette approche permet une plus grande flexibilité ainsi que la possibilité de réutiliser ou adapter le code pour créer plusieurs représentations graphiques.
Nous pouvons par exemple complexifier l'exemple de base de la manière suivante :
# Générer aléatoirement 100 chiffres entre 1 et 100
simulated_data <- sample(1:10, size = 100, replace = TRUE)
# Adapter le graphique avec des arguments
hist(
simulated_data,
main = "Simulation de 100 données entre 1 et 10",
xlab = "Données simulées",
ylab = "Nombre d'occurence",
col = "lightblue",
)
# Ajouter une ligne horizontale avec une valeur de 10
abline(h = 10, col="red", lwd=3, lty=2)
# Ajouter une légende correspondante
legend(
x = "topright",
c("Limite de 10"),
col = c("red"),
lwd = c(3),
lty = c(2)
)
Nous avons apporté les modifications suivantes :
- À la ligne 14, avec la fonction
abline(), nous avons ajouté une ligne horizontale en correspondance de la valeur 10. Cette ligne a des arguments qui en détermine la couleurcol, la largeurlwd, et le type de traitlty; - De la ligne 17 à 23, nous avons ajouté une légende, avec certains arguments (en forme de vecteurs cette fois-ci) qui reprennent les arguments de la ligne horizontale.
Le résultat sera similaire à l'image suivante :
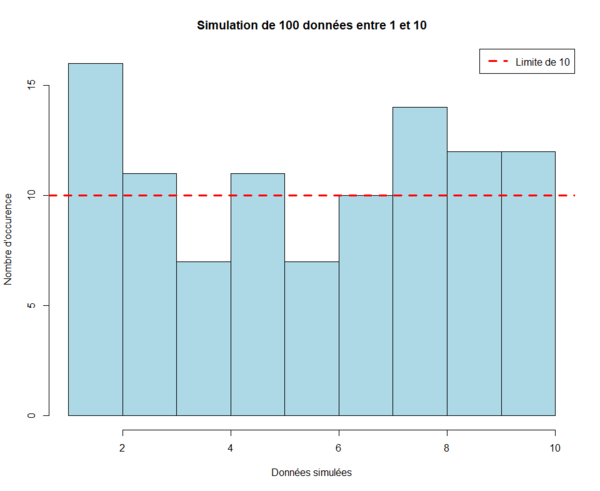
Comme vous pouvez le noter, certains arguments ne sont pas très saillants (e.g. lwd ou lty) et de plus ils sont associés à des chiffres. Il faudrait donc se souvenir à quel type de trait correspond le chiffre 1, le chiffre 2, etc.
D'autre côté, le fait qu'on puisse générer des graphiques à travers des fonctions permet de combiner les éléments de manière différente, par exemple à l'intérieur d'un paquet qui développe une syntaxe homogène comme ggplot2.
Anatomie computationnelle d'un graphique
Au niveau computationnel, un graphique est le résultat de la combinaison entre données d'Input et instructions qui s'occupent de déterminer les détails spécifique de l'Output. Nous proposons donc d'analyser un graphique en fonction du schéma de base Input-Computation-Output qui est commun à l'ensemble des ressources de la pensée computationnelle avec R.
Format de Input
En utilisant des fonctions pour générer des représentations visuelles, il faut déterminer le format d'Input qui est adéquat à la fonction. La décision du format d'entrée dépend des créateurs des fonctions ou paquets de R qui s'occupent de générer les représentations graphiques, car il n'y a pas de standard universel. Par exemple, les fonctions disponibles out-of-the-box dans R acceptent généralement des vecteurs ; d'autres paquets plus récents, comme ggplot2, requièrent des formats rectangulaires (e.g., data.frame) ; d'autres paquets encore peuvent nécessiter des formats avec des structures multi-dimensionnelles comme dans le format JSON.
D'ailleurs, certains fonctions acceptent ou requièrent des Inputs différents par rapport à des structures des données, comme par exemples des modèles (voir Introduction à la modélisation des données avec R). La fonction plot() du paquet de base graphics en est un exemple :
# Données fictives
fict_data <- data.frame(
minutes_running = c(45, 20, 55, 0, 15, 90, 120, 15, 0, 0, 15, 30),
hours_sleeping = c(5.5, 4.5, 6.5, 4.5, 7, 8, 5, 4, 4, 6, 7, 8)
)
# Plot avec les colonnes du data.frame pour scatterplot
plot(
x = fict_data$minutes_running,
y = fict_data$hours_sleeping,
xlab = "Running minutes per day",
ylab = "Sleeping hours per day"
)
# Modèle de regréssion linéaire sur les données du data.frame
lm.model <- lm(hours_sleeping ~ minutes_running, data = fict_data)
# Disposer 2 graphique par ligne
par(mfrow = c(2,2))
# Afficher les graphiques
plot(lm.model)
La fonction plot(...) des lignes 8 à 13 créent un simple scatterplot en utilisant les données du data.frame fictif :
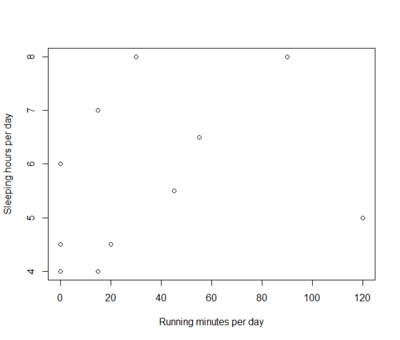
plot()La fonction plot(lm.model) de la ligne 21, par contre, affiche 4 graphiques souvent utilisés pour évaluer les postulats d'une regression linéaire (affichés en deux lignes et deux colonnes grâce à la fonction par(mfrow = c(2,2)) de ligne 19) :
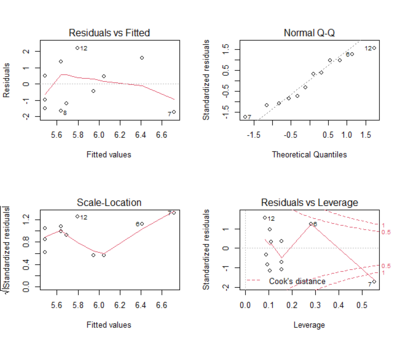
plot()Ce n'est pas important de comprendre les détails ni du modèle de regression, ni des graphiques. Le message à retenir concerne la possibilité de passer en Input autre chose que des données à une fonction qui crée des représentations graphiques.
Computation d'une représentation visuelle
En utilisant des logiciels point-and-click qui créent des graphiques grâce à des manipulations plus ou moins imposées, on peut facilement sous-estimer la computation qui est déclenchée lors de la création d'une représentation graphique. En fonction de la complexité du graphique et des données d'Input, des calculs sont effectués par exemple pour :
- Transformer les données en formes et éléments graphiques
- Les données sont associées avec des propriétés graphiques telles que la position, la couleur, l'opacité, la taille, etc. La computation d'un graphique doit donc implémenter concrètement ces associations.
- Agréger des données
- L'un des avantages des graphiques comparé aux données brutes ou à un tableau consiste à créer des patterns, comme par exemple des regroupements ou des séparations, qui véhiculent de l'information. Sur le même graphique, il est possible de combiner plusieurs agrégation de données à la fois.
- Créer des indices et références visuelles
- Pour faciliter la compréhension de l'information, les graphiques affichent souvent des éléments supplémentaires qui aident à mieux cerner les données, comme par exemple les légendes ou les unités des axes.
- Adapter le contenu aux limites du canvas
- Le graphique occupe un espace - à l'écran ou sur papier - limité, une sorte de toile (ou en termes plus techniques, un canvas). L'ensemble de l'information affiché par le graphique doit donc être ajusté afin que tout puisse être contenu dans les limites du canvas.
Format de Output
La computation du graphique peut aboutir à différents formats de Output qui peuvent différer en fonction du support nécessaire pour les visualiser, leur finalité, ou encore leur extension temporaire. Nous pouvons identifier les formats d'Output suivants :
- Une image matricielle
- Ce type d'image est composé de pixels individuel, dont la couleur de chaque pixel détermine l'affichage globale de l'image. Dans ce contexte, R s'occupe de déterminer comment colorer les pixels qui font partie de la représentation visuelle et de les mettre à disposition à travers une image matricielle, dont les extensions les plus fréquentes sont
.pngou.jpg.
- Ce type d'image est composé de pixels individuel, dont la couleur de chaque pixel détermine l'affichage globale de l'image. Dans ce contexte, R s'occupe de déterminer comment colorer les pixels qui font partie de la représentation visuelle et de les mettre à disposition à travers une image matricielle, dont les extensions les plus fréquentes sont
- Une image vectorielle ou dessin vectoriel
- Ce type de graphique est déterminé à travers de formules mathématiques qui déterminent l'affichage de patterns qui compose le dessin. Dans ce contexte, R s'occupe de déterminer les formules qui représentent les différents éléments qui composent le graphique et les mettre à disposition à travers une image vectorielle, dont le format le plus utilisé est SVG, avec extension
.svg.
- Ce type de graphique est déterminé à travers de formules mathématiques qui déterminent l'affichage de patterns qui compose le dessin. Dans ce contexte, R s'occupe de déterminer les formules qui représentent les différents éléments qui composent le graphique et les mettre à disposition à travers une image vectorielle, dont le format le plus utilisé est SVG, avec extension
- Une animation
- Une animation est créé à travers la succession de différents images qui varient progressivement l'une de l'autre afin de provoquer dans le système visuel l'illusion du mouvement. Une description technique d'une animation est disponible dans la page Animation avec JavaScript. Même s'il s'agit d'un langage différent, les concepts techniques sont les mêmes.
- Une représentation visuelle interactive
- Type de représentation qui permet aux utilisateurs de modifier l'affichage en fonction de leurs actions. Les représentations visuelles interactives sont en général rendues disponibles à travers des pages web, donc avec du HTML5, CSS et JavaScript. La transposition se fait en général automatiquement, donc une connaissance de ces éléments n'est pas nécessaire, mais peut néanmoins s'avérer utile pour des modifications ou intégration dans des contextes plus articulés (e.g. sites web). Une description technique de l'interactivité est disponible dans la page Interactivité avec JavaScript. Le langage est différent, mais les concepts restent les mêmes.
Les représentations visuelles peuvent être enregistrées en tant que fichier (ou ensemble de fichiers), ou intégrées directement dans un document à travers la syntaxe Rmarkdown. Cette deuxième possibilité est particulièrement utile, car elle permet d'adapter les graphiques et disposer toujours de la dernière version du graphique dans le document finale. Pour plus d'informations, voir Introduction à Rmarkdown.
Paquets de R pour la visualisation des données
ggplot2
Le paquet ggplot2 est l'un des paquets les plus utilisés, non seulement dans le contexte académique. Par exemple, la BBC (télévision britannique) utilise ce paquet avec un thème graphique personnalisé pour ces représentations graphiques. ggplot2 fait partie de l'écosystème Tidyverse et est basé sur une grammaire des graphiques qui visent à décomposer les graphiques en différents composantes qui peuvent être déclinés et combinés de différentes manières. Il perment de créer principalement des représentations graphiques statiques, mais qui peuvent définir dynamiques ou interactives grâce à un large écosystème d'extensions et paquets qui l'intègrent. Pour plus d'infos voir :
- sur ce wiki
- Site officiel du paquet
- Extensions de ggplot2
- ggplot2: Elegant Graphics for Data Analysis
Plotly
highcharter
lattice
RGL
DiagrammeR
Leaflet
Conclusion
Ressources
- R Graphics Cookbook, 2nd edition collection de plus de 150 recettes pour la visualisation de données avec R
- Fundamentals of Data Visualization de Claus O. Wilke