Analyse de réseaux avec R
Introduction
L'analyse de réseaux (en anglais, 'network analysis' ou 'NA') est une des approches méthodologiques les plus populaires utilisée en analytique de l'apprentissage (Romero & Ventura, 2020). Poquet et al. (2021) indiquent que l'analyse de réseaux permet la modélisation et l'analyse de données relationnelles en éducation. Un réseau est composé d'un groupe d'entités ou d'éléments appelés noeuds ('nodes') ou sommets ('vertices') et une relation qui les connecte que l'on appelle arêtes ('edge') ou lien ('link'). Ainsi, la visualisation créée via l'analyse de réseaux peut être utile pour cartographier les relations et les interactions, identifier des schémas/patterns d'interaction, identifier les étudiant·e·s actif·ve·s / inactif·ve·s et détecter le rôle de certain·e·s étudiant·e·s ou enseignant·e·s.
Cette page vous montrera un exemple d'analyse de réseaux, montrant le lien entre des étudiant·e·s et la visualisation de leurs exercices. Nous verrons donc quels sont les exercices qui sont le plus visualisés et les liens entre les exercices les plus fréquemment visualisés. De plus, nous aurons aussi une cartographie des étudiant·e·s qui ont besoin de visualiser certains exercices plus que d'autres.
Nous allons utiliser la librairie igraph, librairie la plus accessible pour certain·e·s et la plus téléchargée (voir Figure 1.2 dans https://robwiederstein.github.io/network_analysis/intro.html).
Préparation des données
Téléchargement des données sur votre ordinateur
Les données utilisées proviennent du set 'Data Files for KDD Cup 2010' en accès libre sur DataShop (https://pslcdatashop.web.cmu.edu/Files?datasetId=4524)). Une fois connecté·e à DataShop, téléchargez les données "Algebra I 2005-2006, A development data set; 575 students, 813,661 steps". Décompressez le zip et créez un fichier .R dans le dossier fraichement décompressé 'algebra_2005_2006'.
Importer les données dans RStudio
Ouvrez RStudio et exécutez le code ci-dessous :
rm(list=ls()) # effacer l'environnement
# install.packages("pacman") # à exécuter si pas déjà installé
library(pacman)
pacman::p_load(igraph, # bibliothèques utilisées
dplyr
)
setwd(dirname(rstudioapi::getSourceEditorContext()$path)) # définir le répertoire de travail au répertoire actuel (./algebra_2005_2006/)
data <- read.table("algebra_2005_2006_master.txt", sep="\t", header = T) # importer les donnéesVous devez maintenant avoir dans votre environnement le data frame 'data' avec 3967 obs. de 19 variables
str(data)## 'data.frame': 3967 obs. of 19 variables:
Préparation des 'egdes' et 'nodes'
La première étape afin de créer le réseau est de déterminer la liste des arêtes ('edges') et des noeuds ('nodes'). De ce fait, les colonnes/variables qui vont nous intéresser sont :
Anon.Student.Id: Identifiant (id) de l'étudiant·e, qui servira de noeud (node) = la sourceProblem.Name: Nom de l'exercice, qui servira de noeud (node) = la cibleProblem.View: Nombre de fois où l'exercice a été visualisé, qui servira de poids (weight) dans les liens entre les différents noeuds (étudiant·e - exercice).
Afin de limiter notre visualisation à un nombre restreint de noeuds et ne pas voir l'intégralité des exercices visualisés par les 575 étudiant·e·s de notre jeu de données, nous allons nous intéresser seulement aux exercices qui ont été visualisés plus de 5 fois.
table(data$Problem.View)## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 28 (nombre de visualisation d'un exercice) ## 2930 582 165 103 61 41 19 14 8 12 14 5 2 3 2 1 1 1 1 1 1 (occurence)
Nous allons maintenant créer les data frames edges et nodes qui contiendront les données nécessaires à la création du réseau.
Le data frame edges contiendra obligatoirement en première colonne les noeuds 'sources' en deuxième colonne les noeuds 'cibles' (ce qui formera les arêtes/liens). Toutes les colonnes supplémentaires (à partir de la troisième colonne) seront considérées comme des attributs, voir plus bas. Ici, on extraira de nos données l'attribut de 'poids' qui est le nombre de fois où l'étudiant·e a visualisé l'exercice.
edges <- data.frame(data$Anon.Student.Id, data$Problem.Name, data$Problem.View) %>%
rename(source = data.Anon.Student.Id,
target = data.Problem.Name,
weight = data.Problem.View) %>%
filter(weight > 5)
head(edges)## source target weight ## 1 2oNLCndtam EG61 10 ## 2 46z59pQP58 LIT78A 6 ## 3 52vEY7f17k EG58 7 ## 4 8rsfNQdio8 EG63A 6 ## 5 668lBbaKFE EG22 6 ## 6 668lBbaKFE EG44 9
On voit donc que l'étudiant·e "2oNLCndtam" a regardé l'exercice "EG61" 10 fois.
Le data frame nodes_s contiendra la liste de tous les étudiant·e·s. De même, le data frame nodes_p contiendra la liste de tous les exercices. La première colonne contiendra obligatoirement tous les noeuds. Toute colonne supplémentaire (à partir de la deuxième colonne) sera considérée comme un attribut. Ici, on y ajoutera en deuxième colonne le 'nom court' des noeuds qui sera montré dans le réseau.
nodes_s <- data.frame(unique(data$Anon.Student.Id)) %>%
mutate("name" = paste0("s", row.names(.))) %>%
rename(id = unique.data.Anon.Student.Id.)
nodes_p <- data.frame(unique(data$Problem.Name)) %>%
mutate("name" = paste0("p", row.names(.))) %>%
rename(id = unique.data.Problem.Name.)Le data frame nodes réunit les deux data frames créés précédemment tout en gardant les noeuds filtrés dans le data frame edges.
nodes <- rbind(nodes_s, nodes_p) %>%
filter(id %in% edges$source | id %in% edges$target)
head(nodes)## id name ## 1 2oNLCndtam s3 ## 2 46z59pQP58 s4 ## 3 52vEY7f17k s5 ## 4 8rsfNQdio8 s9 ## 5 668lBbaKFE s23 ## 6 PpTLi2Qz8E s33
Nous voyons ici le 'nom court' attribué à chaque étudiant·e.
Création du graphique
Maintenant que les data frames des noeuds et des arêtes ont été créés, nous allons dresser le graphique correspondant grâce à la fonction graph_from_data_frame(d =..., vertices = ..., directed = TRUE qui prend en arguments d = ... le data frame des noeuds (nodes), vertices = ... le data frame des arêtes (edges) et directed = TRUE pour signifier la direction qui part des noeuds des étudiant·e·s aux noeuds d'exercices. L'exécution de la fonction plot() suivant donnera le graphique ci-après :
g <- graph_from_data_frame(d = edges, vertices = nodes, directed = TRUE) set.seed(42) plot(g)
"Pas très joli" 🤔, me direz-vous. En effet, faisons en sorte de le rendre plus lisible grâce aux fameux attributs.
Attributs
Les attributs seront tous les paramètres des noeuds et arêtes qui peuvent être modifiés afin de rendre le réseau plus lisible. Quasiment tout peut être modifié : la taille, la couleur, les labels, etc. On peut aussi les changer selon une condition (par exemple montrer les noms des noeuds seulement lorsqu'ils sont reliés à d'autres noeuds de façon forte). Avant de modifier, voyons quels attributs sont déjà présents dans notre graphique g.
Visualisation des attributs
- La fonction
E(): permet de voir les arêtes/liens ('Edges') du graphique créég. On peut lui assigner des attributs directement avec$(voir plus bas).
- La fonction
edges_attr(): permet de voir les attributs des arêtes ('Edges) du graphique créég. Si vous exécutez cette commande et avez suivi le tutoriel, vous verrez que$weightest montré :
edge_attr(g)## $weight ## [1] 10 6 7 6 6 9 (...)
- Il s'agit du nom de la troisième colonne de notre data frame
edges! Voyez-vous le lien ? La fonctiongraph_from_data_frame()a traduit la troisième colonne de le data frameedgescomme étant un attribut weight.
- Il s'agit du nom de la troisième colonne de notre data frame
- La fonction
V(): permet de voir les noeuds ('Vertices') du graphique créég. On peut lui assigner des attributs directement avec$(voir plus bas).
- La fonction
vertex_attr(): permet de voir les attributs des noeuds ('Vertices) du graphique créég. Si vous exécutez cette commande et avez suivi le tutoriel, vous verrez que$nameest montré :
vertex_attr(g)## $name ## [1] "s3" "s4" "s5" "s9" "s23" (...)
- Il s'agit du nom de la deuxième colonne de notre data frame
nodes! Voyez-vous le lien (bis) ? La fonctiongraph_from_data_frame()a traduit la deuxième colonne de le data framenodescomme étant un attribut name.
- Il s'agit du nom de la deuxième colonne de notre data frame
Modification des attributs
Je ne présente ici que quelques exemples de modifications d'attributs, il existe bien d'autres façons de modifier son graphique et là est la force de R !
width
Vous pouvez ajouter un attribut à E(g) comme si c'était un data frame. Ci-dessous, $weight est un attribut que l'on avait déjà avant pour les arêtes et on crée à présent width comme étant le log()+1 de weight (qui est, pour rappel, le nombre de visualisation d'un exercice pour chaque étudiant·e). Cela va permettre de modifier l'épaisseur des arêtes.
E(g)$width <- log(E(g)$weight) + 1 set.seed(42) plot(g)
size
Changeons à présent la taille des noeuds. Pour les noeuds, pensez bien à la commande V(g). Ci-dessous, strength(g) correspond à la somme des visualisations (weight) par noeud.
V(g)$size <- log(strength(g)) * 4 set.seed(42) plot(g)
label (+ ifelse)
Afin de rendre le réseau plus lisible, nous allons émettre une condition de type 'if...else' pour afficher ou non le nom court de l'étudiant·e ou de l'exercice. Si la somme des visualisations par noeud est supérieure à 25 alors on garde le nom du noeud, sinon on ne l'affiche pas.
V(g)$label <- ifelse(strength(g) >= 25, V(g)$name, NA) # show name only when strength >= 75 set.seed(42) plot(g)
Ça commence a être mieux, voyez l'utilité d'assigner un nom court aux noeuds.
color (+ %in%)
Nous allons maintenant attribuer la couleur rouge aux noeuds associés aux étudiant·e·s et la couleur dorée aux noeuds des exercices. En créant la liste des étudiant·e·s et la liste des exercices, il suffit d'assigner à V(g)$color la couleur correspondante, suivant si le nom se trouve dans la liste etudiant ou exercice.
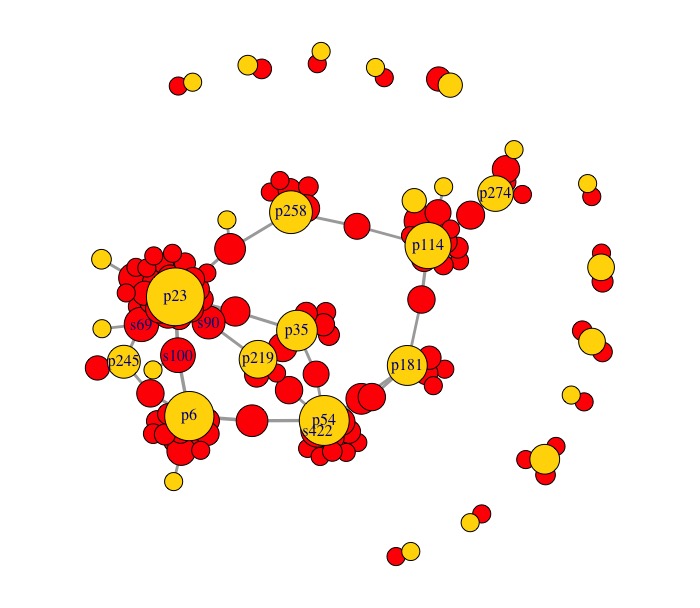
etudiant <- nodes_s$name exercice <- nodes_p$name V(g)$color <- NA V(g)$color[V(g)$name %in% etudiant] <- "red" V(g)$color[V(g)$name %in% exercice] <- "gold" set.seed(42) plot(g)
Nous pouvons maintenant voir les interactions entre étudiant·e·s et exercices assez clairement. En effet, les exercices p23, p6 et p54 semblent être les trois exercices les plus visualisés. Si nous partons de l'hypothèse que plus un exercice est visualisé, plus il suscite de la difficulté chez l'étudiant·e, alors un conseil pour l'enseignant·e serait de revoir soit la façon dont ces exercices sont présentés, soit le cours associé à ces exercices.
De plus, certains étudiant·e·s sont pointé·e·s (s69, s90, s100, s422), montrant alors que ces dernier·ère·s ont un peu plus de difficultés (ou un autre problème) que leurs camarades. Il serait donc conseillé pour l'enseignant·e de faire attention à ces étudiant·e·s afin de les aider au mieux.
Enfin, la structure générale montre aussi d'autres patterns qu'il serait nécessaire d'approfondir : quels sont les étudiant·e·s qui ont du mal avec plusieurs exercices (ex. entre p114 et p181), quel est le point commun entre les exercices qui sont pointés : même matière ? même thème ? moment de l'année ?
Types de graphiques
D'autres types de graphiques peuvent être créés, voici une petite liste de ce qui peut se faire :
par(mfrow=c(2, 3), mar=c(0,0,1,0)) set.seed(42) plot(g, layout=layout_randomly, main="Aléatoire") set.seed(42) plot(g, layout=layout_in_circle, main="Cercle") set.seed(42) plot(g, layout=layout_as_star, main="Etoile") set.seed(42) plot(g, layout=layout_as_tree, main="Arbre") set.seed(42) plot(g, layout=layout_on_grid, main="Grille") set.seed(42) plot(g, layout=layout_with_fr, main="Force-directed") # fruchterman-reingold par(mfrow=c(1,1), mar=c(0,0,0,0))
La fonction plot() utilise donc par défaut l'algorithme de Fruchterman-Reingold, ce dernier étant le plus communément utilisé, il permet de créer des arêtes de même longueur et se croisent le moins possible. Ainsi, les noeuds sont dispersés de manière uniforme et on peut aussi voir que les noeuds qui partagent les mêmes connexions sont plus proches entre elles (voir https://yunranchen.github.io/intro-net-r/igraph.html#layouts pour d'autres dispositions 'force-directed').
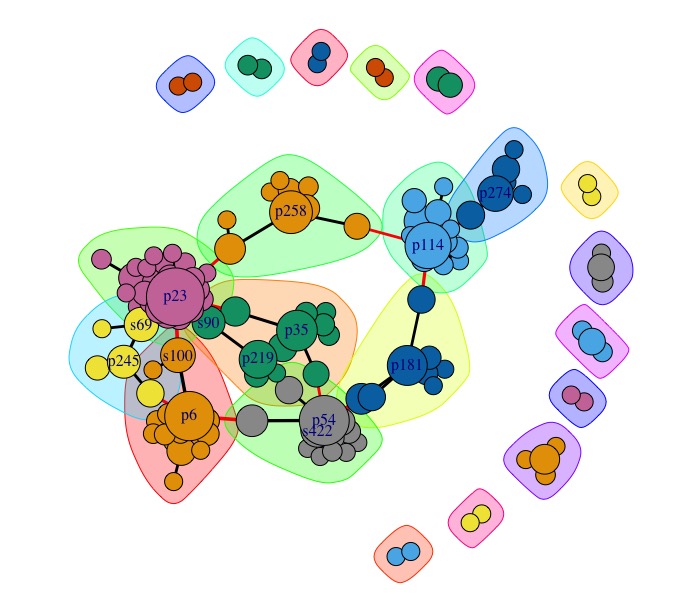
Un dernier type de graphique qui va être montré ici sera le type 'détection de communauté' (en anglais, community detection). Grâce à ce type de graphique, on pourra voir plus précisément les noeuds qui sont densément connectés entre eux (formant des groupes/'communautés'). La fonction cluster_edge_betweenness() va permettre cela :
cnet <- cluster_edge_betweenness(g)
set.seed(42)
plot(cnet,
g)Pour d'autres graphiques de ce type, voir https://yunranchen.github.io/intro-net-r/igraph.html#community-detection
Analyse critique de l'outil - Limites
La première limite à cet outil est l'accessibilité, en outre il faudra être un minimum à l'aise avec la syntaxe de R et savoir comment l'utiliser de manière basique. La page EduTechWiki Premiers_pas_avec_R est un bon point de départ pour commencer avec R.
Une autre limite de cet outil est le caractère flou de la façon dont ces graphiques sont créés. Malgré le fait de reproduire les mêmes graphiques (reproducibilité), il reste difficile pour l'utilisateur·trice novice de déterminer pourquoi certains noeuds sont plus visibles que d'autres. Il faudra donc être prudent quant à l'utilisation et la lecture de vos graphiques. En l'occurence, il sera judicieux de savoir exactement ce que signifient vos noeuds, vos arêtes et le poids que vous leur donnez. Comme le disent Poquet et al. (2021), la construction d'un réseau dépend des choix faits par les chercheur·euse·s, en outre les choix de ce qui est étudié (noeuds), quelles interactions vont être choisies (liens) et comment la force entre les liens doit être considérée (poids). Ces choix influencent la manière dont le réseau est construit et impactent indirectement l'interprétation du/de la chercheur·euse.
Une dernière critique sera le caractère quantitatif, en terme de recherche quantitative, de cet outil. Précédemment, j'ai émis le postulat selon lequel 'plus de visualisation amène à plus de difficulté' mais il se peut que ce ne soit pas du tout le cas (par exemple, un bug dans le système de récupération des données). Le cadre théorique devra suffisamment être bien justifié pour définir ce genre de postulat. Au pire, l'interprétation sera écrite avec précaution, au mieux, une analyse qualitative viendra s'ajouter aux résultats afin de mieux justifier le postulat.
Recommandations quant à l'utilisation de cet outil
Selon Poquet et al. (2021) :
- Quels sont les noeuds (nodes) et leur pertinence face au contexte, à la théorie, ou la question de recherche ?
- Quels sont les liens (edges), et que représentent-ils ? Quelles sont les hypothèses liées à la définition de vos liens et quelles sont vos justifications ?
- Est-ce que le réseau est orienté, non-orienté ou mixte ?
- Est-ce que le réseau est pondéré ? Est-ce que le réseau est filtré ou simplifié selon un certain seuil ? Si oui, comment justifiez-vous ce seuil ?
- Comment les arêtes, le poids, et la direction sont en adéquation avec le contexte, la théorie et l'interprétation ?
- Est-ce que le réseau est unipartite ou bipartite ?
- Si les arêtes étaient agrégées; quelle est la durée pendant laquelle l'agrégation a été faite ?
- Quel logiciel, et quelle version, a été utilisé pour calculer les indices du réseau ? Quels algorithmes ou équations ont été implémentés dans le logiciel pour calculer ces indices ?
- Quel logiciel a été utilisé pour la visualisation du réseau ? Quelle configuration de réseau a été utilisé ?
- Qu'avez-vous utilisé en terme de méthode de détection de communauté, d'algorithme et de paramètres ?
- Quelle est la taille du réseau: le nombre de noeuds et d'arêtes dans chaque réseau étudié; y a-t-il des éléments isolés, ont-il été exclus de l'analyse et pourquoi ?
- Dans la communication des réseaux qui ont été construit à partir de données d'événements, est-ce que le temps (discret ou continue) et la fréquence des échanges on été inclus dans la construction du réseau ou la modélisation statistique; si non, pourquoi avez-vous exclu cette information ?
- Selon quel cadre (p.ex., contexte d'apprentissage, design pédagogique) le réseau a-t-il été développé ? En quoi ce cadre se distingue des autres études reportées ?
Références
Koedinger, K.R., Baker, R.S.J.d., Cunningham, K., Skogsholm, A., Leber, B., Stamper, J. (2010) A Data Repository for the EDM community: The PSLC DataShop. In Romero, C., Ventura, S., Pechenizkiy, M., Baker, R.S.J.d. (Eds.) Handbook of Educational Data Mining. Boca Raton, FL: CRC Press.
Poquet, O., Saqr, M., & Chen, B. (2021). Recommendations for network research in learning analytics: 2021 NetSciLA Workshop “Using Network Science in Learning Analytics: Building Bridges towards a Common Agenda”, NetSciLA 2021. CEUR Workshop Proceedings, 2868, 34–41.
Romero, C., & Ventura, S. (2020). Educational data mining and learning analytics: An updated survey. Wiley Interdisciplinary Reviews-Data Mining and Knowledge Discovery, 10(3). https://doi.org/10.1002/widm.1355
Saqr, M., & Alamro, A. (2019). The role of social network analysis as a learning analytics tool in online problem based learning. BMC medical education, 19(1), 160. https://doi.org/10.1186/s12909-019-1599-6
Liens
- Base de données
- https://pslcdatashop.web.cmu.edu/Files?datasetId=4524 (Base de donnée 'Data Files for KDD Cup 2010' via DataShop)
- Tutoriels
- https://yunranchen.github.io/intro-net-r/igraph.html (le plus complet)
27 mars 2022 à 23:27 (CEST)