« Création d'échelles composées » : différence entre les versions
mAucun résumé des modifications |
|||
| (Une version intermédiaire par le même utilisateur non affichée) | |||
| Ligne 2 : | Ligne 2 : | ||
|fait_partie_du_cours=Manuel de recherche en technologie éducative | |fait_partie_du_cours=Manuel de recherche en technologie éducative | ||
|fait_partie_du_module=Statistiques descriptives et échelles | |fait_partie_du_module=Statistiques descriptives et échelles | ||
|pas_afficher_sous-page=Non | |||
|page_precedente=Statistiques descriptives | |page_precedente=Statistiques descriptives | ||
|page_suivante=Analyse de données quantitatives | |page_suivante=Analyse de données quantitatives | ||
| Ligne 7 : | Ligne 8 : | ||
|dernière_modif=2015/08/27 | |dernière_modif=2015/08/27 | ||
|difficulté=débutant | |difficulté=débutant | ||
|voir_aussi=Validation de questionnaire | |||
|all_pages_module=Non | |||
}} | }} | ||
----- | ----- | ||
| Ligne 67 : | Ligne 70 : | ||
* Lorsque les distributions sont très différentes de la normale, (e.g. une courbe en forme de J), d'autres méthodes de standardisation peuvent être utilisées, puisque dans la transformation de Fisher, il est considéré que la moyenne et l'écart-type décrivent correctement la centralité (l'individu type) et la dispersion (la déviation type des individus). | * Lorsque les distributions sont très différentes de la normale, (e.g. une courbe en forme de J), d'autres méthodes de standardisation peuvent être utilisées, puisque dans la transformation de Fisher, il est considéré que la moyenne et l'écart-type décrivent correctement la centralité (l'individu type) et la dispersion (la déviation type des individus). | ||
=== La qualité d'une échelle === | === [[Validation de questionnaire | La qualité d'une échelle]] === | ||
A nouveau, nous souhaiterions répéter que vous devriez utiliser '''''un ensemble d'items publié pour mesurer une variable''''' (si disponible). Ce faisant, vous pouvez éviter de fournir de longues justifications! | A nouveau, nous souhaiterions répéter que vous devriez utiliser '''''un ensemble d'items publié pour mesurer une variable''''' (si disponible). Ce faisant, vous pouvez éviter de fournir de longues justifications! | ||
Dernière version du 18 avril 2022 à 10:33
| Manuel de recherche en technologie éducative | |
|---|---|
| Module: Statistiques descriptives et échelles | |
| ◀▬▬▶ | |
| ⚐ brouillon | ☸ débutant |
| ⚒ 2022/04/18 | ⚒⚒ 2015/08/27 |
| Voir aussi | |
ATTENTION : BROUILLON - Daniel K. Schneider (discussion) 26 août 2015 à 19:15 (CEST)
Création d'échelles composées (indices)
Les échelles composées mesurent un concept théorique, e.g. la sensation d'être là (présence sociale) ou la confiance en ses compétences TIC ou l'utilisation d'ordinateurs en classe. De tels concepts ne peuvent être mesurés directement, c'est pourquoi ils sont aussi appelés variables latentes. Pour mesurer de telles variables implicites "molles" avec des questionnaires, plusieurs questions sont posées. Elles peuvent alors être combinées en une variable composite unique, aussi appelée indice ou échelle.
Nous pouvons faire la distinction entre deux sortes d'échelles, ou indices, composites:
- Les indices qui résument des mesures non nécessairement fortement corrélées, e.g. des compétences globales en informatique.
- Les indices qui sont unidimensionnels, i.e. ils mesurent le même concept théorique.
Il existe de nombreuses formes d'échelles et nous ne traiterons ici que de leurs formes les plus simples.
Echelles simples basées sur des moyennes
La plupart des échelles sont construites simplement en calculant les moyennes des différentes questions qui utilisent la même gamme d'items de réponse, e.g. une échelle de 1 à 5. Ces dernières sont parfois dénommées "échelles de Likert".
Utilisez la procédure suivante:
- Eliminez les questions qui ont un nombre élevé de non-réponses
- Assurez-vous de ne pas prendre en compte les valeurs manquantes (non-réponses) lorsque vous additionnez les réponses des différents items. Un vrai programme de statistiques (SPSS) le fait pour vous.
Lorsque vous créez votre questionnaire, ou que vous utilisez les données d'un sondage de quelqu'un d'autre, assurez-vous que toutes les questions utilisent la même gamme d'items de réponse, autrement vous devrez standardiser (voir ci-dessous). Il n'y a pas de sens à calculer les moyennes d'échelles à cinq points avec des items d'échelles à dix points!
Vous ne pouvez pas simplement additionner toutes sortes de questions et déclarer que le résultat est un indice d'une variable théorique. Les questions qui sont utilisées pour calculer un indice devraient mesurer la même variable ou dimension théorique. Vous pouvez justifier théoriquement votre choix d'items et/ou (mieux encore) vous pouvez démontrer que les questions sont fortement corrélées.
Echelles standardisées à variable centrée réduite
Vous devrez parfois utiliser des échelles standardisées. Une formule de standardisation répandue est la transformation de Fisher (coefficient de corrélation), qui produit ce que l'on appelle la variable centrée réduite, aussi dénommée score Z, note réduite, résultat type, note typique, ponctuation standard ou score centré réduit. La formule pour calculer une note réduite pour un individu est la suivante:
note réduite = écart de l'individu / écart-type note réduite = ( Xi - moyenne ) / écart-type
Les notes réduites peuvent être facilement comparées, car une note réduite indique la distance entre une moyenne et un résultat particulier en termes d'écart-type.
- La moyenne est toujours égale à 0
- L'écart-type est toujours égal à 1
En d'autres termes, les notes réduites montrent dans quelle mesure un individu est différent en termes de distribution globale. Cet écart, ou différence, est exprimé en termes de N écarts-types. E.g. un résultat de 2 indique qu'un individu donné est 2 fois l'écart-type au-dessus de l'individu moyen dans l'échantillon.
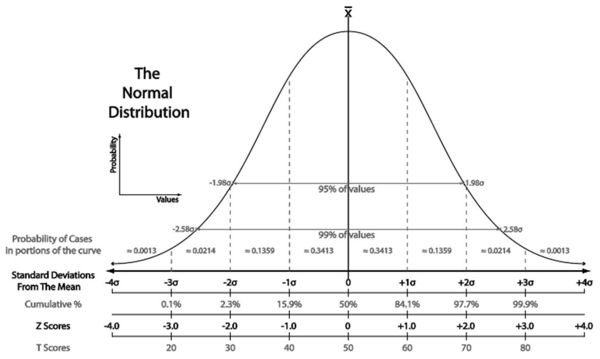
La Figure 5 (tirée de Wikipédia) compare les différentes mesures de la distribution normale: écarts-types, pourcentages cumulés, notes réduites, et cotes normalisées. Cette figure indique que 70% de la population se trouve au sein de l'intervalle de l'écart-type. Au-dessus de l'ET +1, un individu est dans les 15% les plus hauts et au-dessous de l'ET -1, il/elle se trouve parmi les 15% les plus bas. Les notes réduites devraient habituellement êtres répartis entre -3 et 3.
Il peut sembler difficile de penser en termes de moyenne=0 et d'écart-type=1 et il existe des variations esthétiques comme les cotes normalisées. Les cotes normalisées sont calculées avec la formule suivante et sont utilisées dans l'espoir de faciliter la compréhension, en référence au schéma familier du "pourcent".
- Cote normalisée=note réduite*10+50
La moyenne est de 50 et l'écart-type est de 10. L'étude PISA 2006 a utilisé un schéma de résultat de test avec une moyenne=500 et un écart-type=100.
Remarques:
- Il est important de comprendre que dans de nombreuses méthodes statistiques, il est considéré que les données sont distribuées normalement. Ces méthodes sont dites paramétriques. Les statistiques non paramétriques ne requièrent pas d'hypothèses relatives à la distribution des données.
- Les notes réduites maintiennent le coefficient d'aplatissement et l'asymétrie, i.e. l'analyse statistique paramétrique mènera aux même résultats, que vous standardisiez ou non. La standardisation des variables dont les échelles sont différentes est obligatoire pour le calcul des échelles composées ou de l'analyse typologique.
- Aux Etats-Unis, les notes réduites sont utilisées pour comparer les étudiants de différentes écoles, car dans certaines écoles il existe ce que l'on appelle une inflation des notes (les résultats types varient seulement entre A et B), ce qui n'est pas le cas dans d'autres écoles.
- Lorsque les distributions sont très différentes de la normale, (e.g. une courbe en forme de J), d'autres méthodes de standardisation peuvent être utilisées, puisque dans la transformation de Fisher, il est considéré que la moyenne et l'écart-type décrivent correctement la centralité (l'individu type) et la dispersion (la déviation type des individus).
La qualité d'une échelle
A nouveau, nous souhaiterions répéter que vous devriez utiliser un ensemble d'items publié pour mesurer une variable (si disponible). Ce faisant, vous pouvez éviter de fournir de longues justifications!
Un premier critère est la sensibilité: les résultats du questionnaire devraient refléter la réalité. Par exemple, si la recherche exploratoire a montré un degré plus élevé de présence dans un type d'environnement d'apprentissage que dans un autre, les résultats d'un questionnaire de présence devraient le montrer.
Un deuxième critère est l'unidimensionnalité (une sorte de fiabilité de l'échelle): la cohérence interne entre les items utilisés pour construire une échelle qui mesure la même variable latente (concept théorique) doit être élevée. Il existe plusieurs méthodes pour tester cela. La plus répandue est le coefficient alpha de Cronbach. Il mesure le degré auquel les réponses sont corrélées les unes aux autres. Selon Garson, "Si l'alpha est supérieur ou égal à 0,6, alors les items sont considérés comme unidimensionnels et peuvent être combinés dans un indice ou une échelle. Certains chercheurs utilisent la limite plus stricte de 0,7".
Un troisième critère est lié à la validité des variables: les résultats obtenus avec le questionnaire peuvent être liés à d'autres mesures, i.e. similaires à des résultats obtenus par d'autres outils (e.g. entretiens approfondis). De plus, les résultats devraient être corrélés avec des variables quantitatives similaires.
Exemple: Le COLLES
Le sondage sur les environnements d'apprentissage constructivistes en ligne Constructivist On-Line Learning Environment Surveys (COLLES) mesure l'expérience de l'utilisateur dans une unité d'enseignement. Cet outil de sondage comprend 24 affirmations mesurant 6 dimensions.
- Nous ne montrerons que les deux premières dimensions (i.e. quatre questions concernant la pertinence et quatre questions concernant la réflexion).
- Remarque: dans le véritable questionnaire, vous ne montrerez pas les labels comme "Items concernant la pertinence" ou "codes de réponse".
| Affirmations | Presque jamais | Rarement | Parfois | Souvent | Presque toujours |
|---|---|---|---|---|---|
| codes de réponse | 1 | 2 | 3 | 4 | 5 |
| Items concernant la pertinence | |||||
| a. mon apprentissage se focalise sur des questions qui m'intéressent. | O | O | O | O | O |
| b. ce que j'apprends est important pour ma pratique professionnelle en tant que formateur(trice). | O | O | O | O | O |
| c. j'apprends comment améliorer ma pratique professionnelle en tant que formateur(trice). | O | O | O | O | O |
| d.ce que j'apprends est vraiment en lien avec ma pratique professionnelle en tant que formateur(trice). | O | O | O | O | O |
| Items concernant la réflexion | |||||
| ... Je porte un regard critique sur la façon dont j'apprends. | O | O | O | O | O |
| ... Je porte un regard critique sur mes propres idées. | O | O | O | O | O |
| ... Je porte un regard critique sur les idées des autres étudiants. | O | O | O | O | O |
| ... Je porte un regard critique sur les idées émises lors des lectures. | O | O | O | O | O |
L'algorithme pour calculer chaque échelle est simple: pour chaque individu, ajoutez les codes de réponse et divisez le tout par le nombre d'items que vous avez. Assurez-vous de ne pas ajouter des "valeurs manquantes". Par conséquent, une meilleure méthode est d'utiliser la fonction moyenne dans votre logiciel, car ce dernier prendra automatiquement en compte le fait que vous pouvez avoir des valeurs manquantes:
Pertinence = moyenne (a, b, c, d)
Exemple – L'individu A, qui a répondu a=parfois, b=souvent, c=presque toujours, d= souvent, donne:
(3 + 4 + 5 + 4) / 4 = 4
Exemple – L'individu B, qui a répondu a=parfois, b=souvent, c=presque toujours, d=manquant, donne:
(3 + 4 + 5) / 3 = 4
Et certainement pas:
(3 + 4 + 5 + 0) / 4 ou (3 + 4 + 5 -1) / 4
La conception d'échelles est facile si vous savez comment utiliser votre programme de statistiques. E.g. dans SPSS vous trouverez l'outil de calcul de variables dans le menu: Transformer -> Calculer la variable.
Echelles de vraisemblance maximum pondérées
Il existe des modèles plus complexes pour concevoir des échelles, tout particulièrement celles utilisées dans la théorie des items de réponse. Un exemple type de recherche est le PISA (Programme international pour le suivi des acquis des élèves). Les études PISA ont lieu tous les trois ans et recueillent des informations sur des élèves de 15 ans dans les pays participants. Le principal objectif du PISA est de déterminer le niveau de préparation des élèves face aux défis à venir, plutôt que leur niveau de maîtrise d'un programme particulier. (OCDE 2009, avant-propos).
L'évaluation PISA produit deux types de données:
- Evaluation des compétences dans différents domaines (items cognitifs), e.g. le PISA 2006 couvrait la lecture, les mathématiques et les sciences. L'étude principale comprenait aussi des questions attitudinales.
- Données contextuelles (questionnaire sur l'environnement familial des élèves, questionnaire sur l'école et questionnaire facultatif pour les parents)
"Les questionnaires contextuels du PISA 2006 comprenaient de nombreux items sur les caractéristiques des élèves, leur environnement familial, leurs perceptions, les caractéristiques de l'école et la perception des directeurs de l'école. Dans 16 pays, des questionnaires pour les parents (facultatifs) ont été adressés aux parents des étudiants testés. Certains des items étaient conçus pour être utilisés dans des analyses comme des items uniques (par exemple le genre). Cependant, la plupart des items du questionnaire étaient conçus pour être combinés d'une certaine manière de façon à mesurer des construits latents qui ne peuvent pas être observés directement. Pour ces items, des procédures de transformation ou d'ordination sont nécessaires pour élaborer des indices significatifs" (OECD 2009: 304).
Pour calculer des indices, le PISA emploie des modèles d'ordination basés sur des méthodologies de la théorie des items de réponse (Item response theory, IRT). Cette modélisation par items de réponse est basée sur les estimations de vraisemblance pondérées, qui sont difficiles à comprendre. Nous n'en rapporterons ici que le principe général.
“On peut estimer l'aptitude relative d'élèves à passer un test en particulier en observant la proportion d'items de test auxquels ils répondent correctement. La difficulté relative des items dans un test peut être estimée en observant dans quelle proportion les participant(e)s au test répondent correctement à chaque item. Le modèle mathématique employé pour analyser les données du PISA, généré à partir d'un design de test rotationnel dans lequel les élèves accomplissent des tâches différentes mais se chevauchant, est mis en œuvre au moyen d'un logiciel d'analyse de test utilisant des procédures itératives pour estimer simultanément la probabilité qu'une personne en particulier répondra correctement à un item de test donné, et la probabilité qu'un item de test en particulier fera l'objet d'une réponse correcte par un(e) élève donné. Le résultat de ces procédures est un ensemble d'estimations qui permettent de définir un continuum, qui est une réalisation de la variable à laquelle on s'intéresse. Sur ce continuum, il est possible d'estimer la position de chaque élève, ce qui permet de voir dans quelle mesure chaque élève peut expliquer ou décrire la variable de connaissances, et il est possible d'estimer la position de chaque item de test, ce qui permet de voir dans quelle mesure chaque item incarne la variable de connaissances. Ce continuum est appelé échelle globale des connaissances PISA dans les domaines pertinents de test de la lecture, des mathématiques ou des sciences. […]
Pour chacune de ces variables de connaissances, une ou plusieurs échelles sont définies, qui vont de niveaux de connaissances très bas à des niveaux très élevés. Lorsqu'on se demande ce qu'une telle échelle signifie en termes de compétences de l'étudiant(e), on peut observer qu'un(e) étudiant(e), dont l'estimation des aptitudes le (la) situe sur un certain point sur l'échelle de connaissances PISA, serait très probablement capable d'accomplir avec succès des tâches situées sur ce point de l'échelle ou plus bas. Il/elle serait probablement de plus en plus capable d'accomplir des tâches à mesure que l'on descend sur l'échelle, mais serait probablement moins capable d'accomplir des tâches situées au-dessus de ce point de l'échelle, et probablement de moins en moins capable d'accomplir des tâches à mesure que l'on progresse vers le haut de l'échelle." (OECD 2009:284).
Le PISA 2006 a utilisé deux sortes d'échelles.
(1) Les échelles de test PISA sont normalisées avec une moyenne de 500 et un écart-type de 100, e.g. une sorte de variante de l'échelle de cote normalisée. Ces dernières sont aussi appelées échelles PISA. Par exemple, le niveau de culture scientifique mesure en quelque sorte les aptitudes globales en sciences, mais pas seulement. Il englobe aussi un modèle multifactoriel de compétences cognitives liées au domaine. L'échelle prend en compte:
- le degré de transfert et d'application de savoirs requis
- le degré d'exigence cognitive requis pour analyser la situation présentée et synthétiser une réponse appropriée:
- le degré d'analyse nécessaire pour répondre à la question
- le degré de complexité nécessaire pour résoudre le problème présenté:
- the degree of complexity needed to solve the problem presented (REPETITION dans le texte source)
- le degré de synthèse nécessaire pour répondre à la question
Il existe pour chacun de ces facteurs des items de test qui mesurent différents niveaux de difficulté. E.g. le test S485Q05(2) Pluies acides, au niveau de difficulté élevé de 717 points, "requiert que le rôle d'un contrôle dans une expérience scientifique soit compris et explicitement reconnu. Une aptitude à comprendre la structure d'une expérience (i.e. la démarche scientifique) est un pré-requis" (OECD 2009: 291). A l'autre extrême, le test S213Q02 Vêtements, au bas niveau de difficulté de 399 points, requiert que l'étudiant sache "choisir l'instrument de laboratoire à utiliser pour mesurer un courant électrique". Ces échelles PISA sont alors divisées en 6 bandes (niveaux) pour aider à l'interprétation standardisée des scores nationaux, par exemple.
Définition des bandes pour le niveau de culture scientifique sur l'échelle PISA:
Niveau Points de score sur l'échelle PISA
6 Au-dessus de 707.9 5 de 633.3 à 707.9 4 de 558.7 à 633.3 3 de 484.1 à 558.7 2 de 409.5 à 484.1 1 de 334.9 à 409.5
La distribution des sujets suit une courbe normale en forme de cloche, e.g. seuls 1,3% atteignent le niveau 6 (au-dessus de 707,9 points).
(2) Certains indices contextuels ont été construits grâce à de simples transformations arithmétiques (e.g. moyennes).
(3) La plupart des indices contextuels ont été calculés une fois encore au moyen d'une technologie d'ordination IRT utilisant les estimations de vraisemblance pondérées (logits). Les items du questionnaire étaient soit dichotomiques, soit de type Likert (habituellement avec quatre ou cinq items de réponse). Ces indices étaient normalisés autour de la moyenne de 0 de tous les pays de l'OCDE avec un écart-type de 1. Dans ce cas également, nous n'expliquerons pas comment ces échelles ont été calculées, mais nous présenterons simplement un exemple ci-dessous qui concerne le degré de familiarité avec les TIC.
Exemples PISA
Familiarité avec les TIC dans l'étude PISA 2006
"Le questionnaire de familiarité avec les TIC était un instrument optionnel qui a été administré dans 40 des pays participant au PISA 2006, pour lequel quatre indices normés ont été calculés" (PISA 2006 Technical Report, OECD 2009). Nous examinerons cet exemple en détail, aussi dans l'objectif de montrer une nouvelle fois quels items de questionnaire pourraient être utilisés pour construire des variables d'indice (échelles mesurant des variables théoriques).
Ces échelles ont été conçues avec logit (estimations pondérées de la vraisemblance maximum [weighted maxium likelihood estimations, WLE]). Elles ont été standardisées comme échelles standards avec la moyenne OCDE = 0 et l'écart-type OCDE = 1.
Les valeurs issues du questionnaire ont été inversées, de façon à ce que les valeurs plus élevées soient "meilleures". L'inversion signifie que la valeur la plus basse d'une échelle devient la plus haute, et inversement, comme le montre l'exemple suivant, un item du questionnaire à propos de la "navigation Internet". Habituellement, on conçoit un questionnaire de façon à ce que les réponses soient dans le "bon" ordre, i.e. les "scores élevés" sont associés aux "valeurs élevées".
Pour ces items de réponse inversés, quatre indices ont été calculés:
- Utilisation d'Internet/divertissement TIC (INTUSE).
- Utilisation de programmes/logiciels TIC (PRGUSE)
- Confiance en soi dans les tâches TIC Internet (INTCONF)
- Confiance en soi dans les tâches TIC de haut niveau (HIGHCONF)
Ces indices peuvent être utilisés pour comparer les pays ou les autres sous-populations. Nous présenterons succinctement les quatre indices ci-dessous et soulignerons quelques différences intéressantes dans la distribution.
Utilisation d'Internet/divertissement TIC
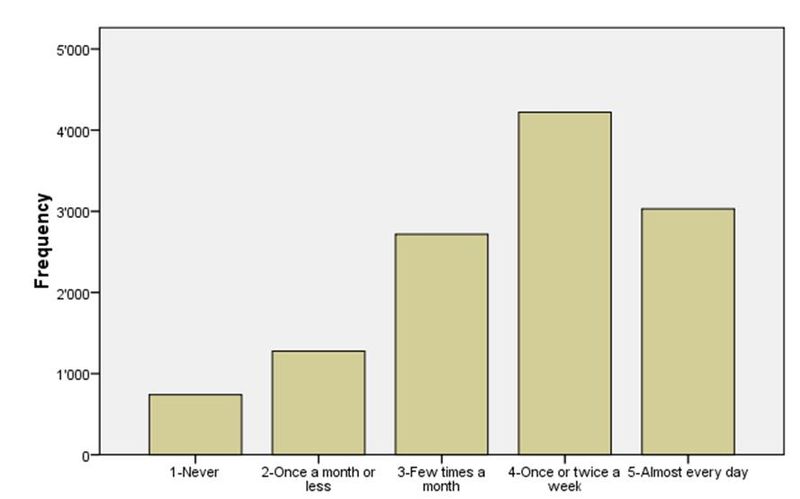
Un des indices (échelle composée) calculés était l'utilisation Internet/divertissement TIC (INTUSE). Il comprend six items de question formulés ainsi:
IC04Q01 a) Surfer sur Internet pour chercher des informations à propos de personnes, de choses ou d'idées
IC04Q02 b) Jouer avec des logiciels de jeu
IC04Q04 d) Utiliser Internet pour collaborer avec un groupe ou une équipe
IC04Q06 f) Télécharger des logiciels (y compris des logiciels de jeu) sur Internet
IC04Q09 i) Télécharger de la musique sur Internet
IC04Q11 k) Communiquer (e.g. échanger du courrier électronique ou participer à des salons de discussion ("chat rooms"))
Chaque item était mesuré avec une échelle à cinq points:
(1) Presque tous les jours
(2) Une ou deux fois par semaine
(3) Quelques fois par mois
(4) Une fois par mois ou moins
(5) Jamais
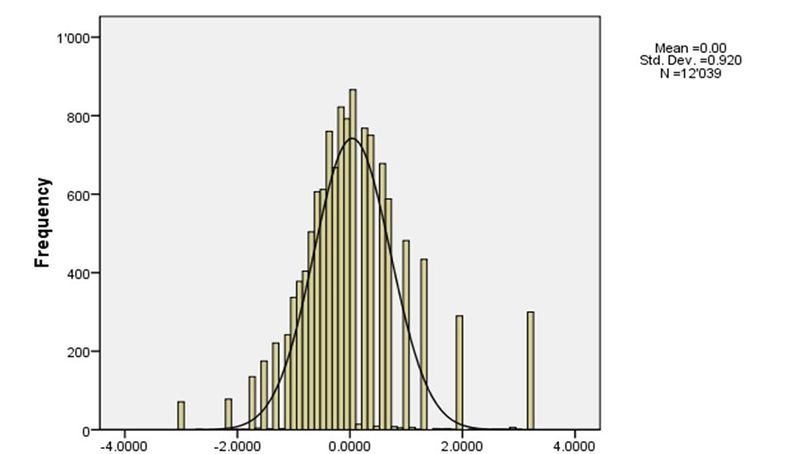
La Figure 8 montre la distribution de la fréquence. Comme vous pouvez le constater, la distribution est plutôt "en forme de cloche", mais il y a des extrêmes sur la gauche (pratiquement jamais) et sur la droite (très souvent). A partir de ce type d'indice, il n'est pas possible de savoir exactement quelle est la contribution des différents items de question. D'autre part, les points de donnée de -4/+4 ne peuvent pas être traduits en scores de question individuelle. Ils représentent les écarts-types OCDE. E.g. une valeur de 3,5 signifie qu'un étudiant a un score de 3,5 fois les écarts-types OCDE au-dessus de la moyenne. En d'autres termes, c'est un étudiant tout à fait brillant.
Statistiques | ||
INTUSE TIC Utilisation d'Internet/divertissement PISA 2006 (WLE) | ||
N | Valide | 12039 |
N | Manquant | 153 |
Moyenne | -.001633 | |
Médiane | -.143800 | |
Mode | .0889 | |
Ecart-type | .9198212 | |
Asymétrie | .841 | |
Coefficient d'aplatissement | 2.712 | |
Intervalle | 6.2201 | |
Minimum | -3.0404 | |
Maximum | 3.1797 | |
Somme | -19.6627 | |
Centiles | 25 | -.555500 |
| 50 | -.143800 |
| 75 | .363400 |
Dans de nombreuses études, on utilise la méthode plus simple consistant à calculer la moyenne des items du questionnaire. Statistiquement parlant, c'est une moins bonne solution, car les items de réponse (Presque tous les jours, Une ou deux fois par semaine, Quelques fois par mois, Une fois par mois ou moins, Jamais) forment une échelle ordinale type. Certains avancent par conséquent que la moyenne n'est pas un descripteur optionnel de la centralité des réponses d'un individu. Par ailleurs, calculer une simple moyenne est beaucoup plus facile. Dans ce cas, la différence entre les deux indices n'est pas trop importante et ils sont hautement corrélés (r=933). Cependant, utiliser la simple moyenne crée une courbe "plus aplatie".
Corrélations | |||
| INTUSE TIC Utilisation d'Internet/divertissement PISA 2006 (WLE) | INTUSE_MEANS TIC Utilisation d'Internet/divertissement PISA 2006 (Moyennes) | |
INTUSE ICT Utilisation d'Internet/divertissement PISA 2006 (WLE) | Corrélation de Pearson | 1 | .933 |
Sig. (2-tailed) |
| .000 | |
N | 12039 | 12039 | |
INTUSE_MEANS ICT Utilisation d'Internet/divertissement PISA 2006 (Moyennes) | Corrélation de Pearson | .933 | 1 |
Sig. (2-tailed) | .000 |
| |
N | 12039 | 12039 | |
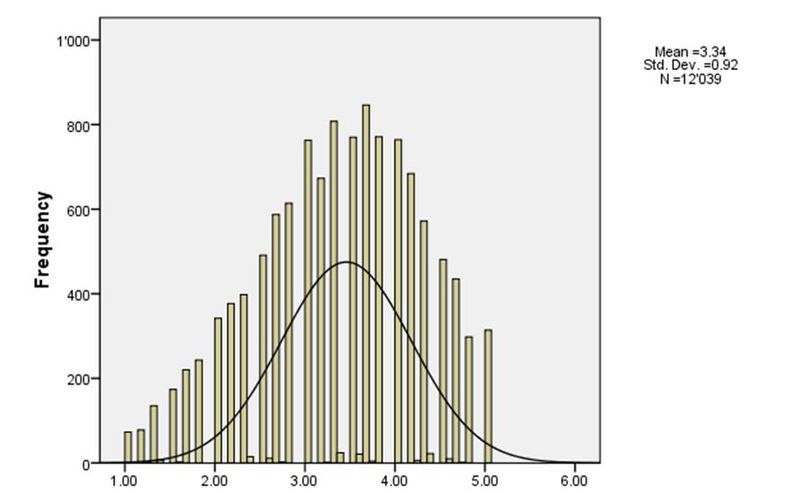
Ci-dessous vous trouverez les statistiques de résumé et l'histogramme pour la variable de l'indice INTUSE_MEANS Utilisation d'Internet/divertissement TIC PISA 2006 (Moyennes).
Statistiques | ||
INTUSE_MEANS TIC Utilisation d'Internet/divertissement PISA 2006 (Moyennes) | ||
N | Valide | 12039 |
N | Manquant | 153 |
Moyenne | 3.3448 | |
Médiane | 3.4000 | |
Mode | 3.67 | |
Ecart-type | .92046 | |
Variance | .847 | |
Asymétrie | -.309 | |
Coefficient d'applatissement | -.549 | |
Intervalle | 4.00 | |
Minimum | 1.00 | |
Maximum | 5.00 | |
Centiles | 25 | 2.6667 |
| 50 | 3.4000 |
| 75 | 4.0000 |
L'élève type a un score de 3,4 (médiane) et l'élève moyen un score de 3,3 (moyenne). Cela se traduit à peu près par "plusieurs fois par semaine", un élève utilise Internet à des fins de divertissement. Il y avait 6 questions allant de "Surfer sur Internet pour chercher des informations à propos de personnes etc." à "Communiquer". Si un élève répond à chaque question quelque chose comme Une ou deux fois par semaine ou Quelques fois par mois, il/elle obtiendra ce genre de moyenne, mais on ne peut en être certain. Le même étudiant pourrait mener certaines activités presque tous les jours et d'autres activités beaucoup moins.
Pour s'assurer qu'une batterie d'items de question mesure le même construit théorique (i.e. l'utilisation d'Internet à des fins de divertissement), on peut calculer un coefficient appelé alpha de Cronbach. Dans notre cas, l'alpha est de 0,725, ce qui est suffisant mais pas remarquable.
Utilisation de programmes/logiciels TIC
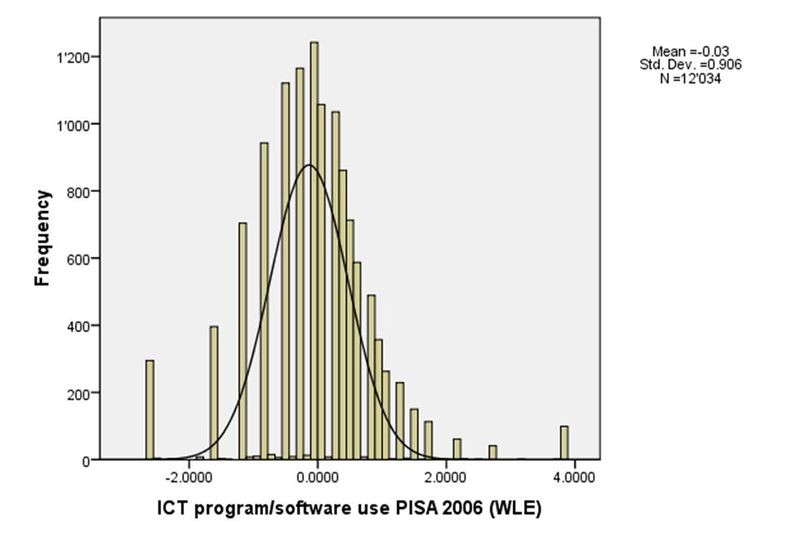
Les items pour l'indice Utilisation de programme/logiciel TIC (PRGUSE) utilisaient les mêmes items de réponse que INTUSE, et comprenaient 5 questions:
- IC04Q03 c) Ecrire des documents (e.g. <Word ou WordPerfect>
- IC04Q05 e) Utiliser des tableurs (e.g. <Lotus 1 2 3 ou Microsoft Excel®>)
- IC04Q07 g) Dessiner, peindre ou utiliser des programmes de graphisme
- IC04Q08 h) Utiliser des logiciels éducatifs tels que des programmes pour les mathématiques
- IC04Q10 j) Ecrire des programmes informatiques
Statistiques | ||
PRGUSE utilisation de programme/logiciel PISA 2006 (WLE) | ||
N | Valide | 12034 |
N | Manquant | 158 |
Moyenne | -.025253 | |
Médiane | .077700 | |
Mode | -.0969 | |
Ecart-type | .9063436 | |
Asymétrie | .220 | |
Coefficient d'aplatissement | 2.788 | |
Intervalle | 6.4050 | |
Minimum | -2.5771 | |
Maximum | 3.8279 | |
Somme | -303.8948 | |
Centiles | 25 | -.526100 |
| 50 | .077700 |
| 75 | .521700 |
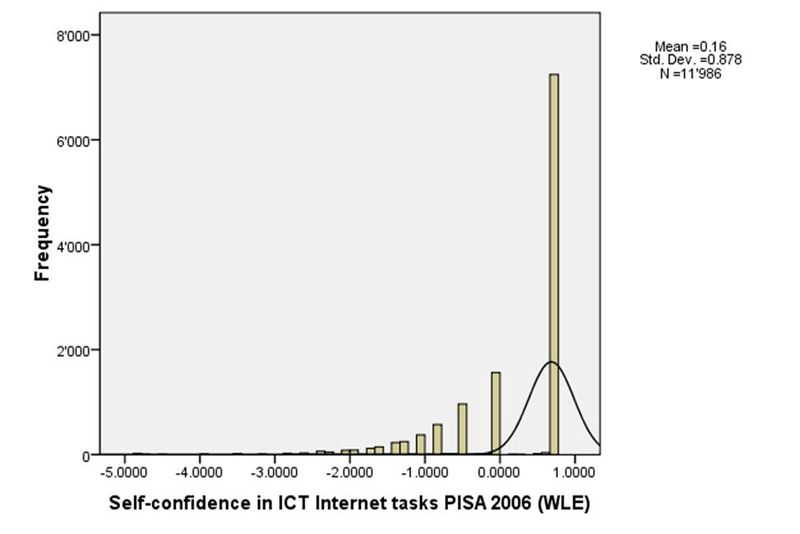
6.3 Confiance en soi dans des tâches Internet TIC
Un troisième indice a été calculé pour la confiance en soi dans les tâches Internet TIC (INTCONF). Les items étaient encore un fois mesurés avec une échelle à quatre points:
- 1. Je peux le faire très bien par moi-même
- 2. Je peux le faire avec l'aide de quelqu'un
- 3. Je sais ce que cela veut dire mais je ne peux pas le faire
- 4. Je ne sais pas ce que cela veut dire
Les questions faisant partie de l'indice étaient les suivantes:
- IC05Q01 a) "Chatter" en ligne
- IC05Q07 g) Chercher des informations sur Internet
- IC05Q08 h) Télécharger des fichiers ou des programmes sur Internet
- IC05Q09 i) Joindre un fichier à un courrier électronique
- IC05Q13 m) Télécharger de la musique sur Internet
- IC05Q15 o) Rédiger et envoyer des courriers électroniques (E-mails)
Statistics | ||
INTCONF Confiance en soi dans les tâches Internet TIC PISA 2006 (WLE) | ||
N | Valide | 11986 |
N | Manquant | 206 |
Moyenne | .164309 | |
Médiane | .763800 | |
Mode | .7638 | |
Ecart-type | .8781368 | |
Asymétrie | -1.569 | |
Coefficient d'aplatissement | 2.809 | |
Intervalle | 5.6179 | |
Minimum | -4.8541 | |
Maximum | .7638 | |
Somme | 1969.4109 | |
Ces données suggèrent que la majorité de la population possède un niveau similaire. La médiane (0,76) est beaucoup plus élevée que la moyenne (0,16). Cela suggère également qu'une certaine partie de la population a de vraies difficultés par rapport à la population "type". Cependant, cet indice INTCONF ne permet pas vraiment d'interpréter les valeurs absolues. Une simple échelle additive comme celle que nous avons calculée ci-dessus serait plus utile. Puisque l'INTCONF est ordiné par rapport à la moyenne OCDE, nous pouvons néanmoins comparer les pays à la fois en termes de centralité et de modèles de distribution.
Confiance en soi dans les tâches TIC de haut niveau
Enfin, la confiance en soi dans les tâches TIC de haut niveau (HIGHCONF) a été mesurée avec les questions suivantes, qui utilisent les mêmes items de réponse qu'INTCONF.
- IC05Q02 b) Utiliser un logiciel pour détecter les virus et les supprimer
- IC05Q03 c) Modifier des photos numériques ou d'autres éléments graphiques 1.01
- IC05Q04 d) Créer une base de données (e.g. en utilisant <Microsoft Access>
- IC5Q10 j) Utiliser un logiciel de traitement de texte (e.g. pour rédiger un travil pour l'école)
- IC05Q11 k) Utiliser un tableur pour tracer une courbe
- IC05Q12 l) Créer une présentation (e.g. en utilisant <Microsoft PowerPoint>)
- IC5Q14 n) Créer une présentation multimédia (avec du son, des images, des vidéos)
- IC5Q16 p) Créer une page web
Statistiques | ||
HIGHCONF Confiance en soi dans les tâches TIC de haut niveau PISA 2006 (WLE) | ||
N | Valide | 11978 |
N | Manquant | 214 |
Moyenne | .094825 | |
Médiane | .039400 | |
Mode | .4864 | |
Ecart-type | .9579116 | |
Asymétrie | .156 | |
Coefficient d'aplatissement | .793 | |
Intervalle | 6.0901 | |
Minimum | -3.9905 | |
Maximum | 2.0996 | |
Somme | 1135.8184 | |
Ces échelles sont assez bien corrélées, comme nous en discuterons dans l'article sur l'analyse de données exploratoires.
Résumé
- Les techniques d'analyse des données descriptives sont principalement utilisées pour préparer des analyses plus poussées.
- Cependant, elles peuvent être utilisées comme preuves dans des études de terrain plus qualitatives ou dans des designs de systèmes comparatifs.
Pour pratiquer:
- Quelle est la différence entre une moyenne et une médiane? Laquelle est plus représentative du cas type
- Quels coefficients peuvent être utilisés pour détecter les distributions non normales?
- Quand devient-il obligatoire d'utiliser des résultats types (z-scores) dans l'analyse?
- Citez trois principaux types de données.
Pour pratiquer:
Etude de cas
- Téléchargez les résultats du PISA 2006 depuis le site web: http://www.pisa.oecd.org/
- Comparez les résultats des élèves en science entre la Jordanie, le Qatar et la Tunisie. Expliquez quelles sortes d'informations vous avez utilisées et justifiez vos choix.
- Remarque: Cet exercice exige de vous que vous soyez capable d'identifier le document approprié sur un site web.