Statistiques descriptives
| Manuel de recherche en technologie éducative | |
|---|---|
| Module: Statistiques descriptives et échelles | |
| ◀▬▬▶ | |
| ⚐ brouillon | ☸ débutant |
| ⚒ 2015/09/02 | ⚒⚒ 2015/08/27 |
Vue d'ensemble des statistiques descriptives
Comme mentionné précédemment, les statistiques descriptives résument les distributions de données, i.e. elles vous fournissent un résumé de comment se présentent les valeurs d'une variable ou d'un ensemble de variables donné. Nous pouvons distinguer trois sortes de résumés de statistiques descriptives, comme nous allons le voir ci-dessous.
Coefficients qui mesurent la tendance centrale d'une variable
Ces coefficients donnent une certaine idée du point de donnée le "plus typique" ou le "plus représentatif". E.g., sur une échelle de notation de 0 à 100, l'étudiant moyen aurait 80 points.
- La moyenne est la mesure la plus courante. Calculer une moyenne n'a de sens que pour les variables à intervalles.
- La médiane est le point de donnée qui se trouve au milieu des valeurs "basses" et "hautes", i.e. près de 50% de l'échantillon a des valeurs plus élevées et près de 50% a des valeurs plus basses. On peut l'utiliser aussi bien avec les variables à intervalles qu'avec les variables ordinales.
- Le mode est la valeur la plus fréquemment rencontrée, i.e. le point le plus haut dans un histogramme ou le plus gros secteur d'un diagramme circulaire. A utiliser avec des variables nominales ou ordinales.
Les moyennes sont significatives seulement pour les données à intervalles; la médiane peut être utilisée aussi bien pour les données à intervalles que pour les données ordinales. On peut utiliser le mode pour toute échelle, mais est utilisé habituellement avec les données ordinales et nominales.
Graphiques
- Les histogrammes peuvent être utilisés avec tous les types de données
- Les diagrammes circulaires peuvent être utilisés à la place des histogrammes, mais ils comprennent moins d'informations.
Nous présenterons quelques histogrammes ci-dessous.
Coefficients mesurant la dispersion d'une variable
- L'écart-type (ET) est la déviation moyenne par rapport à la moyenne, i.e. la moyenne de toutes les différences par rapport à la moyenne. L'ET est égal à la racine carrée de la variance.
- La variance est la moyenne des distances au carré. On l'utilise pour calculer des statistiques complexes mais rarement pour des interprétations directes. On préfère l'ET car son unité est la même que celle de la variable d'origine.
- Les valeurs sommets et creux sont les extrêmes à chaque bout d'un intervalle ou d'une échelle ordinale.
- Les quartiles se basent sur les mêmes principes que la médiane. Ils définissent les points pour les intervalles d'1/4 (25%, 50% and 75% de la population)
Mesures de normalité
- De nombreuses procédures statistiques requièrent une distribution normale des données. Comme nous l'expliquerons ci-dessous, les distributions normales sont symétriques et ont une courbe en forme de cloche. Environ 70% des données devraient se situer dans un écart-type (ET) de la moyenne et 95% devraient se situer dans deux écarts-types.
- L'asymétrie est une inclinaison vers la gauche ou la droite. La partie asymétrique est aussi appelée queue. Selon Garson, l'asymétrie devrait être comprise entre +2 et -2 lorsque les données sont distribuées normalement. Certains auteurs utilisent une gamme de +1 à -1 comme critère plus strict lorsque la normalité est critique. Ci-dessous, un exemple d'une distribution asymétrique avec une queue à gauche de l'indice de la confiance en soi dans les tâches TIC liées à Internet, tiré de l'étude PISA 2006. Le coefficient d'asymétrie est de -1,2.

Cette figure montre qu'un grand nombre d'élèves se sentent confiants face à des tâches Internet simples.
- Le coefficient d'aplatissement mesure la forme en "pic" d'une distribution. Le coefficient d'aplatissement de Fisher, très répandu, établit la normalité à zéro. Selon Garson, “un test empirique commun pour la normalité est de recourir aux statistiques descriptives pour obtenir l'asymétrie et le coefficient d'aplatissement, puis d'utiliser le critère selon lequel le coefficient d'aplatissement doit être compris entre +2 et -2 lorsque les données sont distribuées normalement (quelques auteurs utilisent la gamme plus tolérante de +3 à -3, alors que d'autres utilisent la gamme de +1 à -1 comme critère plus strict lorsque la normalité est critique). Un coefficient d'aplatissement négatif indique un nombre trop élevé de cas dans les queues de la distribution. Un coefficient d'aplatissement positif indique un nombre trop bas de cas dans les queues." Dans notre exemple, le coefficient d'aplatissement est de 1,3.
Dans les exemples tirés du PISA 2006 ci-dessous, vous verrez d'autres distributions avec différentes sortes d'asymétrie et de coefficient d'aplatissement.
- Les valeurs atypiques éventuelles sont souvent définies comme des cas qui sont encore plus éloignés de la moyenne que trois écarts-types, mais il existe d'autres définitions. Si vous disposez de petits ensembles de données (e.g. participants à un cours de formation), de telles valeurs atypiques peuvent altérer considérablement les résultats et vous devriez y faire bien attention. Dans des échantillons énormes qui ont des scores de test conçus comme les études PISA, seulement 1,3% des étudiants sont au niveau de maîtrise 6 (708 points) dans les tests d'alphabétisation, i.e. about 2 standard definitions apart, et très peu seulement sont au-dessus de 800 points. En d'autres termes, vous n'avez pas à vous inquiéter pour les valeurs atypiques éventuelles dans de telles études car (a) le test a été conçu pour avoir une distribution "normale" et la taille de l'échantillon est énorme, ce qui élimine l'importance relative des extrêmes.
Ci-dessous, vous trouverez les fréquences de l'une des échelles des sciences pour tous les étudiants. La courbe noire représente la "distribution normale" potentielle.

Graphiques et données combinés
La boîte à moustache est un graphique répandu. Il montre différentes informations, comme les quartiles. En outre, il montre les valeurs atypiques éventuelles, i.e. les valeurs extrêmes. Nous présenterons cette technique dans le chapitre sur l'analyse exploratoire des données.
Exemple de distribution tiré de l'étude PISA 2006
Nous illustrerons les résumés de statistiques descriptives avec des variables tirées de l'étude PISA 2006. Nous avons extrait les étudiants suisses. Ce sous-échantillon comprenait environ 12'000 individus, ce qui est un échantillon énorme, comparé aux études habituelles en technologie éducative.
Nous avons observé la question de sondage suivante, issue de la Composante Familiarité avec les TIC du questionnaire pour les étudiants.
- Q4 A quelle fréquence utilisez-vous les ordinateurs pour les raisons suivantes?
- (e) Utiliser les feuilles de calcul sur tableur (e.g. <Lotus 1 2 3 ® ou Microsoft Excel ®>)
- Les items de réponse possibles étaient les suivants
- presque tous les jours
- Quelques fois par semaine
- Entre une fois par mois et une fois par semaine
- Moins d'une fois par mois
- Jamais
Dans l'ensemble de données SPSS, cette variable s'appelle IC04Q05 Use spreadsheets IC4e et la distribution ressemble à cela:
IC04Q05 Use spreadsheets IC4e | ||||
| Fréquence | Pourcent | Pourcent valide | Pourcent cumulé |
1 Presque tous les jours | 571 | 4.7 | 4.8 | 4.8 |
2 Une ou deux fois par semaine | 1806 | 14.8 | 15.1 | 19.9 |
3 Quelques fois par mois | 3024 | 24.8 | 25.3 | 45.2 |
4 Une fois par mois ou moins | 3181 | 26.1 | 26.6 | 71.8 |
5 Jamais | 3377 | 27.7 | 28.2 | 100.0 |
Total | 11959 | 98.1 | 100.0 |
|
Manquant | 7 N/A | 10 | .1 |
|
8 Invalide | 24 | .2 |
|
|
9 Manquant | 199 | 1.6 |
|
|
Total Manquant | 233 | 1.9 |
|
|
Total | 12192 | 100.0 |
| |
Sur 12'192 élèves, 11959 réponses sont valides. La catégorie la plus large est celle des élèves qui n'ont jamais utilisé une feuille de calcul (28.2%). Peu d'élèves seulement les utilisent souvent, i.e. presque tous les jours (4.7%).
Voici certaines des statistiques:
Statistiques - IC04Q05 Use spreadsheets IC4e | ||
Valide N | 11959 | |
Manquant | 233 | |
Moyenne | 3.58 | |
Médiane | 4.00 | |
Mode | 5 | |
Ecart-type | 1.182 | |
Asymétrie | -.397 | |
Coefficient d'aplatissement | -.818 | |
Gamme | 4 | |
Minimum | 1 | |
Maximum | 5 | |
Somme | 42864 | |
Centiles | 25 | 3.00 |
| 50 | 4.00 |
| 75 | 5.00 |
L'élève le plus représentatif (mediane) a un score de 4, i.e. il/elle utilise une feuille de calcul une fois par mois ou moins.
Ci-dessous se trouvent deux sortes d'histogrammes. Un diagramme à colonnes, qui montre les items de réponse, et un graphique de fréquence, qui montre certaines informations statistiques, outre la courbe de distribution normale attendue.
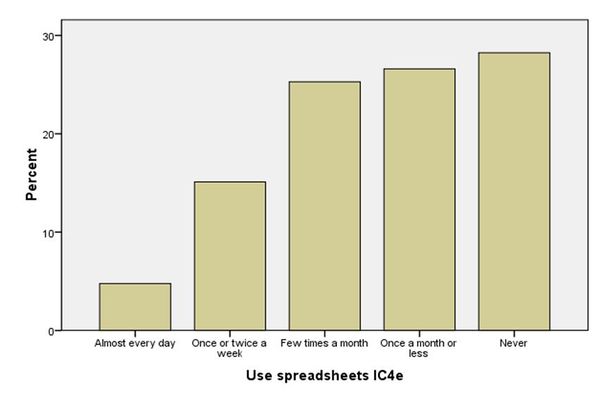

On peut faire valoir que certaines statistiques comme la moyenne, l'écart-type, le coefficient d'aplatissement, et l'asymétrie ne devraient pas être utilisées pour des variables ordinales dans l'analyse. Cependant, en statistiques descriptives, ces coefficients fournissent des informations utiles. Vous devez seulement faire attention lorsque vous interprétez. E.g. une moyenne de 3,58 dans l'utilisation de feuilles de calcul signifie que l'utilisateur moyen se trouve entre "quelques fois par mois" et "une fois par mois ou moins", i.e. régulièrement mais vraiment pas souvent. La médiane (4) est d'une interprétation plus sûre: l'étudiant type utilise une feuille de calcul une fois par mois ou moins.
Il est toujours plus sûr d'interpréter des données à intervalles réelles, e.g. des indices prédictifs sophistiqués qui ont été construits à partir de plusieurs items de questionnaires et que nous présenterons ci-dessous.