« Clustering et classification hiérarchique en text mining » : différence entre les versions
(→k-mean) |
|||
| (94 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{ | {{tutoriel | ||
|fait_partie_du_cours=Analytique et exploration de données | |||
|fait_partie_du_module=Text mining | |||
|statut=à finaliser | |||
|voir_aussi=Méthodes de classification en text mining, Text mining | |||
|cat tutoriels=Analytique et exploration de données | |||
|difficulté=intermédiaire | |||
}} | |||
==Le Clustering == | |||
Le partitionnement de données (data clustering en anglais) est une des méthodes statistiques d'analyse des données. Elle vise à diviser un ensemble de données en différents « paquets » homogènes, en ce sens que les données de chaque sous-ensemble partagent des caractéristiques communes, qui correspondent le plus souvent à des critères de proximité (similarité). (source: [http://fr.wikipedia.org/wiki/Partitionnement_de_donn%C3%A9es Wikipedia]). | |||
En clair, le clustering cherche à faire des classes telle que | |||
* les différences intra-classe soient minimales pour obtenir des ''clusters'' | |||
* les différences inter-classe soient maximales afin d'obtenir des sous-ensembles bien différenciés. | |||
'''Dans le cas d'un corpus textuel, en général les données sont un ensemble de documents, pour lesquels on utilise un ensemble de termes pour les classer.''' | |||
Le résultat d'une classification prends traditionnellement soit la forme d'un graphique de points ou d'un dendogramme | |||
<gallery widths=250px heights=250px> | |||
Image:avg-linkage.svg | Cluster graph (algorithme EM) - source [https://www.flickr.com/photos/rosenfeldmedia/3344374190/ flikr] | |||
Image:KMeans-Gaussian-data.png | Cluster graph (k-means) - source [http://commons.wikimedia.org/wiki/File:KMeans-Gaussian-data.svg wikimedia] | |||
Image:Dendogram.jpg | Dendogram (classification hiérarchique) - source [http://upload.wikimedia.org/wikipedia/commons/4/4c/EM-density-data.svg wikimedia] | |||
</gallery> | |||
==Définition d'une distance == | ==Définition d'une distance == | ||
Voir [[Text | Dans la plus part des cas, le calcul de la distance entre les documents se base sur la [[Text mining#Les Matrices termes-documents|matrice termes-documents]] qui recense le nombre ou la fréquence d'apartition des termes dans chaque document du corpus. | ||
Voir la page [[Text mining#Similarité|Text mining]] pour un survol. | |||
=== Distance du cosinus=== | |||
La distance la plus couramment utilisée est la distance du '''cosinus''' ou ''cosine'' qui est définie comme | |||
<math> | |||
\cos(i,j) = \frac{i\cdot j}{\lVert i \rVert \lVert j\rVert} | |||
</math> | |||
où <math> i\cdot j</math> dénote le produit scalaire et <math>\lVert . \rVert</math> la norme associée. | |||
Dans la norme euclidienne, cela s'écrit | |||
<math> | |||
\cos(i,j)=\frac{ \sum_{k=1}^{n} i_k\cdot j_k }{ \sqrt{\sum_{k=1}^{n}i_k^2}\cdot \sqrt{\sum_{k=1}^{n} i_k^2}} | |||
</math> | |||
où <math>i_k</math> représente le nombre d'occurrences du terme k dans le document i (tirés par exemple de la [[Text mining#Les Matrices termes-documents|matrice termes-documents]]). | |||
'''Cosine généralisée''' | |||
On peut généraliser la mesure du cosinus en introduisant une fonction de "damping" qui aura pour effet de rendre plus clair les différences (parfois minimes) entre les documents. | |||
Par exemple, souvent on remplace <math>i_k</math> et <math>j_k</math> par le logarithme ou la racine carrée de la fréquence d'apparition du terme k. | |||
C'est-à-dire, si <math>n_k</math> dénote le nombre totale d'occurrences du terme k dans l'ensemble du corpus, on remplace dans la formule <math>i_k</math> par <math>log(i_k/n_k)</math> ou par <math>\sqrt{\left( i_k/n_k \right)}</math> (et de même pour <math>j_k</math>). | |||
[[Fichier:Distance-of-vectors.svg|thumb|none|350px|Trois termes et trois documents - distance entre documents]] | |||
La distance du cosinus est toujours comprise entre -1 et +1 et peut être reliée intuitivement avec la notion de corrélation de la manière suivante : | |||
* plus deux documents sont similaires et plus ils auront tendance à utiliser les mêmes termes. Les termes seront alors corrélés, ce qui se traduit géométriquement par être "colinéaires", c'est à dire par un angle faible entre eux et donc un cosinus proche de +1 ou -1 ; | |||
* inversement, deux documents non similaires auront tendance a avoir des termes décorrélées. Autrement dit, ils seront "orthogonaux" géométriquement et leur cosinus sera proche de 0. | |||
=== Limitations de la distance du cosinus=== | |||
Cette distance est parmi les plus utilisées, cependant elle présente tout de même quelques limitations. | |||
Une des limites de la distance du cosinus est qu'elle ne tient pas compte de la possibilité d'utiliser des synonymes lors de la rédaction du corpus. Si un texte n'utilise que le mot "chien" et un autre que le mot "canidé", leur distance sera considérée comme grande. Ce point peut être résolu en faisant appel à des modifications du corpus comme avec la méthode LSI. | |||
Une limitation plus importante de cette méthode, comme mentionné par [https://perso.uclouvain.be/vincent.blondel/publications/08-textmining.pdf Senellart et Blondel] est que le modèle mathématique sous-jacent repose sur l'hypothèse d'un espace orthogonal, ce qui implique les termes soient globalement répartis uniformément les uns par rapport aux autres dans le corpus, ce qui est rarement le cas puisque le corpus est en principe une collection de document partageant des caractéristiques communes (et donc des similarités). | |||
=== Autres distances possibles === | |||
Il est également possible de définir d'autre distances comme | |||
* la '''distance de cluster''' proposée par Chen et Lynch (1972) qui est une distance asymétrique (si i et similaire à j cela ne veut pas dire que j est similaire à i) et définie par | |||
<math> | |||
\text{clusterdist}(i,j) = \frac{i\cdot j}{\lVert i \rVert_1} | |||
</math> | |||
où <math>\lVert i \rVert_1</math> désigne la norme <math>l_1</math> de i, c'est-à-dire la somme du nombre d'occurrences de chaque termes k dans le document i. | |||
== Autres bases possibles pour la classification == | * les '''mesures de Jaccard''' définies par | ||
D'autres bases existent pour la classification que la définition d'une distance | |||
<math> | |||
\text{jac}(i,j) = \frac{\text{nombre d'attributs présents dans i et j}}{\text{nombre d'attributs présents dans i tout seul, j tout seul ou les deux.}} | |||
</math> | |||
Par exemple, on peut définir une mesure qui soit le quotient du nombre de fois où i et j apparaissent dans la même phrase divisé par le nombre de fois où i et j apparaissent (ensemble ou non). | |||
=== Autres bases possibles pour la classification === | |||
D'autres bases existent pour la classification que la définition d'une distance pour définir la similarité entre deux termes. On peut voir à ce sujet [http://www.charuaggarwal.net/text-cluster.pdf Aggarwal & Zhai] qui distinguent | |||
* la méthode LSI (Latent Semantic Indexing) qui cherche a grouper les termes synonymes avant la classification. A ce sujet, voir [https://perso.uclouvain.be/vincent.blondel/publications/08-textmining.pdf Senellart & Blondel in Berry & Castellanos (2007), p25] | * la méthode LSI (Latent Semantic Indexing) qui cherche a grouper les termes synonymes avant la classification. A ce sujet, voir [https://perso.uclouvain.be/vincent.blondel/publications/08-textmining.pdf Senellart & Blondel in Berry & Castellanos (2007), p25] | ||
* la méthode NMF (Non-negative Matrix Factorisation) dont le but est d'extraire de la matrice termes-documents un ensemble plus restreint de caractéristiques sur lesquelles seront appliqué la classification. | * la méthode NMF (Non-negative Matrix Factorisation) dont le but est d'extraire de la matrice termes-documents un ensemble plus restreint de caractéristiques sur lesquelles seront appliqué la classification. | ||
| Ligne 15 : | Ligne 91 : | ||
ou encore [http://arxiv.org/pdf/physics/0512106v1.pdf Pons & Latapy] au sujet des marches aléatoires. | ou encore [http://arxiv.org/pdf/physics/0512106v1.pdf Pons & Latapy] au sujet des marches aléatoires. | ||
===Méthodes de | ==Principe général == | ||
Le principe général est de regrouper les documents par similarité afin de dégager des classes qui soit au maximum | |||
* homogènes, c'est-à-dire dont les éléments soient similaires entre eux ; | |||
* différenciées, c'est-à-dire que les éléments de classes différentes soient non similaires (en tout cas moins similaires que les éléments internes à leur classe). | |||
Pour ce faire, il existe plusieurs stratégies, chacune avec avantages et inconvénients. | |||
==Regroupement Hiérarchique== | |||
Le concept de base du regroupement hiérarchique est de fusionner successivement les documents en clusters (groupes) puis les clusters entre eux selon leur degré de similarité. | |||
Elle se décompose donc en deux étapes répétées en boucle (jusqu'à ce qu'il ne reste qu'un seul cluster unique) : | |||
# calculer la similarité (distance) entre tous les cluster existant à l'étape en cours ; | |||
# fusionner les deux clusters qui sont les plus similaires. | |||
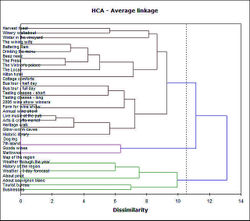
===Présentation des résultats=== | |||
Les résultats du regroupement sont en général présentés sous forme de dendogram : | |||
[[Image:Dendogram.jpg |thumb|none|350px|Dendogram - source [http://upload.wikimedia.org/wikipedia/commons/4/4c/EM-density-data.svg wikimedia] ]] | |||
* sur un axe de coordonnées les documents analysés (ici en vertical) ; | |||
* sur l'autre le degré de similarité (ici en horizontal) ; | |||
* chaque document et cluster est représenté par une ligne (ici horizontale) ; | |||
* lorsque deux lignes sont reliées, c'est que les documents (ou les clusters) correspondant sont fusionnés dans un nouveau cluster. | |||
Plus la ligne horizontale est courte et plus les clusters sont similaires. Cela permet d'avoir une visualisation claire des liens et similitudes entre les éléments. | |||
''Remarque'' : cette représentation n'est pas limitée à l'analyse de texte et se trouve très souvent utilisée, notamment en génétique et biologie pour représenter le degré de similitudes entre les espèces ([http://fr.wikipedia.org/wiki/Arbre_phylog%C3%A9n%C3%A9tique arbre phylogénétique]). | |||
===Choix de méthode de regroupement hiérarchique=== | |||
La difficulté revient alors a bien choisir la façon de calculer le degré de similitude entre deux clusters. | |||
Par exemple, on peut choisir soit le meilleur cas possible, le pire cas possible ou une forme de moyenne. | |||
En général, il s'agit de choisir un ou plusieurs représentants du groupe (cluster) et de calculer la similarité en se basant sur ces représentants. | |||
Pour une visualisation graphique des méthode de classement, voir [http://www.molmine.com/help/algorithms/linkage.htm cette page]. | |||
====Single linkage==== | |||
La méthode du single linkage correspond au choix du "meilleur des cas". | |||
Dans cette méthode, on choisit comme représentant du groupe le document qui est le plus similaire avec les documents de l'autre groupe. | |||
Ainsi la similarité entre les cluster est le '''maximum''' de la similarité entre les documents des clusters. | |||
Le problème principal de cette méthode est que cela peut créer un effet de "chaîne" qui finira par regrouper des éléments qui ne sont pas similaires entre eux. Si A et B sont similaires et B et C sont similiaire, cela ne veut pas dire que A et C sont similaire. | |||
Par exemple, un texte sur la voltige à cheval peut être similaire à un texte sur les chevaux de courses lui-même similaire à un texte sur les courses de vélo qui pourra être similaire à un texte sur l'utilisation du vélo en milieu urbain... | |||
====Complete linkage==== | |||
La méthode du complete linkage est l'opposée du single linkage et correspond au choix du "pire des cas". | |||
Dans cette méthode, on choisit comme représentant du groupe le document qui est le moins similaire avec les documents de l'autre groupe. | |||
Ainsi la similarité entre les cluster est le '''minimum''' de la similarité entre les documents des clusters. | |||
Cette méthode permet d'éviter l'effet de "chaîne" mais en contrepartie est très conservatrice et crée souvent des dendogrammes très alongés (car attribue facilement des similarités faibles). | |||
De plus, elle demande un grande puissance de calcul car elle nécessite un grand nombre de comparaisons à chaque étape de calcul pour déterminer la paire la moins similaire. | |||
====Average linkage==== | |||
Le méthode de l'average linkage est une méthode intermédiaire qui détermine une moyenne (''average'' en anglais) entre les documents des clusters. | |||
Dans cette méthode, on choisit comme similiarité la moyenne des similarités entre toutes les paires d'éléments des clusters considérés. | |||
Ainsi la similarité entre les cluster est la '''moyenne''' de la similarité entre les documents des clusters. | |||
Tout comme la méthode du complete linkage, l'average linkage permet d'éviter l'effet de "chaîne" et de plus, fournit des clusters qui sont souvent de qualité car homogènes (les influences des éléments "extrêmes" se contrebalancent lors de la prise de la moyenne). | |||
En revanche, cette méthode nécessite également une puissance de calcul accrue car il faut considérer toutes les paires possibles lors de chaque étapes de calcul. Pour contourner ce problème on peut ne considérer que le document "moyen" de chaque cluster dans le calcul (et actualiser le choix du document moyen à chaque étape). Cela ne fonctionne pas avec tout les types de les jeux de données (il faut une certaine homogénéité intrinsèque du corpus) mais semble fonctionner particulièrement bien dans le cas de données textuelles (cf . Aggarwal & Zhai, 2012). | |||
C'est donc une '''méthode robuste et qui fonctionne particulièrement bien dans le cadre du text mining.''' | |||
===Exemple=== | |||
Pour un bon exemple d'application de la classification hiérarchique, cette fois au sujet des termes les plus utilisés dans les oeuvres de Shakespeare, on peut voir les deux posts suivants de Andrew Collier : | |||
* [http://www.exegetic.biz/blog/2013/09/text-mining-the-complete-works-of-william-shakespeare/ Text mining the complete work of William Shakespeare] (avec code sous R, en anglais) | |||
* [http://www.exegetic.biz/blog/2013/09/clustering-the-words-of-william-shakespeare/ Clustering the Words of William Shakespeare] (avec code R et package "cluster", en anglais) | |||
[[Image:Shakespeare-dendogram.png |thumb|none |350px| | Dendogram des termes utilisés par Shakespeare - source [http://www.exegetic.biz/blog/2013/09/clustering-the-words-of-william-shakespeare/ exegetic.biz]] | |||
Par exemple, sur le dendograme issu de son analyse, il remarque que le termes "enter", "exeunt" et "scene" vont ensemble, ce qui est certainement du au fait que le découpage traditionnel des scènes de théâtre suit l'entrée (enter) et la sortie (exeunt) des personnages. Nous pouvons également remarquer que "eye" et "love" vont de pair, ainsi que "fear" et "men" ou "keep" et "word", ce qui peut nous conduire a formuler des hypothèses sur le status de la promesse chez Shakespeare (surtout quand on considère les pièces historiques où les trahisons sont légions). | |||
De manière plus macroscopique, on peut également analyser le fait que les termes relatifs à l'amour et aux sentiments forment une classe "à part" clairement séparée du reste des termes du corpus. | |||
=== Résumé de la méthode sous R=== | |||
En partant de la matrice de terme-document et de la distance associée | |||
DTM <- DocumentTermMatrix(doc.corpus) | |||
TDM.dist = dist(TDM.scaled) | |||
on peut utiliser la fonction "agnes" du paquetage "cluster" (dont la [http://cran.r-project.org/web/packages/cluster/cluster.pdf documentation peut être trouvée sur cran.r-project.org]) | |||
pour calculer le dendogramme | |||
library(cluster) | |||
ag.result <- agnes(x = TDM.dist, method = "complete") | |||
et l'afficher avec | |||
plot(ag.result, which.plots = 2, main = "", sub = "", xlab = "") | |||
On peut aussi regarder cette vidéo youtube (en anglais) qui présente le [https://www.youtube.com/watch?v=v3k8WEOVSYw Clustering hiérarchique sous R pour 4 villes]. | |||
==Regroupement basés sur la distance == | |||
Le regroupement basé sur la distance est un ensemble de méthodes dont le but est de réduire le corpus à un nombre de cluster '''fixés à l'avance'''. | |||
Il s'agit donc plus de méthodes de partitionnement du corpus. Bien entendu, puisque le nombre de cluster est fixé à l'avance, il s'agit de bien le choisir. | |||
Heureusement les algorithmes utilisés sont souvent rapides et permettent de "tester" plusieurs nombre de clusters pour déterminer le meilleur. | |||
L'algorithme conne également les équations des droites de différenciation, ce qui permet également de '''classifier un nouveau document''' facilement. | |||
=== Présentation des résultats === | |||
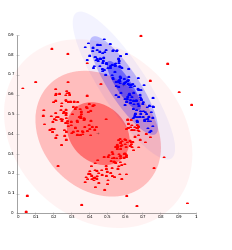
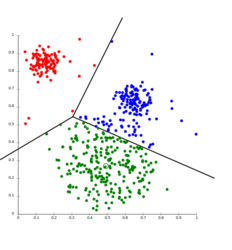
Les résultats sont souvent présentés sous forme de nuage de points comprenant souvent le tracé des lignes "limites" de démarcation entre les clusters. | |||
[[Image:KMeans-Gaussian-data.png |thumb|none |350px| | Cluster graph (k-means) - source [http://commons.wikimedia.org/wiki/File:KMeans-Gaussian-data.svg wikimedia] ]] | |||
Notons que les lignes noires définissent les zones d'attribution à chaque cluster (aussi appelée [http://fr.wikipedia.org/wiki/Diagramme_de_Vorono%C3%AF partition de Voronoi]) et permettent ainsi la classification immédiate d'un document inconnu (il suffit de regarder dans quelle zone il "tombe"). | |||
===k-medoid=== | |||
La méthode k-medoid utilise comme point de départ, pour créer les clusters, un ensemble de documents issus du corpus (appelés medoids ou ancres) et construit les groupes autour. | |||
Dans la phase d'initialisation, chaque document est assigné au medoid qui lui est le plus proche (la plus similaire). | |||
Il s'ensuit alors un processus itératif où la distance moyenne entre les document et le medoid de leur cluster est minimisée, conduisant ainsi à un meilleur regroupement des documents entre eux. | |||
Une itération se décompose en trois étapes : | |||
* On choisit un medoid au hasard et on le remplace par un document choisi au hasard dans le corpus ; | |||
* On recalcule les clusters avec le nouveau medoid et on compare la nouvelle distance moyenne avec l'ancienne distance moyenne ; | |||
* si la nouvelle distance moyenne est meilleure (i.e. plus petite) on conserve le nouveau medoid. | |||
Le processus est alors itéré jusqu'à ce qu'aucune nouvelle substitution n'améliore la classification. | |||
Un inconvénient de cette méthode est sa lenteur de convergence, il faut en général de très nombreuses substitution pour atteindre l'optimum. De plus, un inconvénient majeur est que cette méthode '''ne fonctionne pas très bien avec les données textuelles''' (cf. Aggarwal & Zhai, 2012). En effet, comme le medoid est un document issus du corpus, il ne contient en général pas tout les termes utiles à une classification efficace de la plus part des autres documents (qui auront en général peu de termes communs avec les medoids choisis) car "un document medoid ne contient souvent pas à lui seul tout les concepts requis pour construire un cluster efficacement" ( Aggarwal & Zhai (2012), notre traduction). | |||
===k-mean=== | |||
Basée sur le même type de modèle, la méthode k-means utilise également un ensemble de k représentants (appelées graines ou '''seeds''') autour desquels les clusters sont construits. | |||
Cependant dans ce cas les représentants ne sont pas forcément choisis parmis le corpus mais les graines sont fabriquées et recalculées à chaque étape. En fait, il s'agit de "documents fictifs" contenant une liste de termes avec le "bon" nombre d'occurrences. | |||
En pratique les graines initiales sont souvent choisies parmis les documents du corpus puis les documents sont assignés aux clusters de la graines la plus proche. | |||
Lors de l'itération suivante, les graines sont remplacées par le centroid (calculé) du cluster. | |||
La nouvelle graine est ainsi un document fictif qui contiendrait chacun des termes existant dans une proportion correspondant à la moyenne de la fréquence d'apparition du terme dans le cluster. Par exemple, si un terme apparaît 35 fois dans un cluster de 10 documents alors il apparaîtra (fictivement) 3.5 fois dans la graine. | |||
* Démonstration d'une itération - source [http://en.wikipedia.org/wiki/K-means_clustering wikipedia] : | |||
<gallery widths="150px"> | |||
Image:K Means Example Step 1.png|1) au départ il y a ''k'' graines (rond de couleur, ici''k''=3) | |||
Image:K Means Example Step 2.png|2) Les k clusters sont construits autour des graines (ici avec la [[http://fr.wikipedia.org/wiki/Diagramme_de_Vorono%C3%AF partition de Voronoi]] correspondante). | |||
Image:K Means Example Step 3.png|3) Le centroid de chaque cluster est mis à jour. | |||
Image:K Means Example Step 4.png|4) Le processus itère jusqu'à convergence. | |||
</gallery> | |||
* Pour un exemple d'algorithme k-means, voir le [http://jonathanzong.com/blog/2013/02/02/k-means-clustering-with-tfidf-weights blog de Jonathan Zong] | |||
Une des grandes qualités de la méthode k-means est qu'elle '''converge extrêmement vite, en 5 itérations environ'''. | |||
Un des inconvénient majeur est qu'elle reste dépendante du choix des graines initiales. | |||
Un autre inconvénient est que le centroid calculé (qui sert de nouvelle graine) a tendance à contenir un très grand nombre de termes. En effet il contient l'ensemble de tout les termes qui ont à un moment donné fait partie des documents se trouvant dans le cluster, parfois en très petite proportion, ce qui ralenti beaucoup les calculs. Certaines méthodes existent cependant pour palier à ce problème, comme les méthodes Scatter-Gather ci-dessous. | |||
==== Exemples sous R==== | |||
De nombreux exemples sous R sont disponibles en vidéos, notamment sur youtube par Timothy D'Auria : | |||
* [http://youtu.be/2Znairz-hvU?t=8m4s Analyse de classification et de prédiction pour l'attribution de discours présidentiel à Obama ou à Ronney] | |||
* [https://www.youtube.com/watch?v=j1V2McKbkLo Tutoriel complet pour effectuer une classification par machine learning] | |||
==Autres méthodes== | |||
===Méthodes hybrides : Eclater et regrouper (Scatter-Gather)=== | |||
D'autres méthodes existent dont la mise en oeuvre peut être plus complexe comme | |||
* le '''Buckshot''' qui cherche à améliorer les algorithmes de type ''k-means'' en sélectionnant <math>\sqrt{k\cdot n}</math> graines au lieu de k puis les fusionnent en k graines ; | |||
* la '''Fractionalisation''' qui répartit le corpus en sous-corpus de tailles réduites, réalise une agglomération des corpus pour en réduire le nombre puis classifie le corpus réduit. | |||
===Méthodes basées sur la fréquence des termes=== | |||
D'autres méthodes existent encore, basées entre autres sur la fréquence de présence des termes dans les documents. | |||
Pour de plus amples informations sur ces méthodes, voir [http://www.charuaggarwal.net/text-cluster.pdf Aggarwal et Zhai (2012)] | |||
=== Méthodes probabilistes === | |||
D'autres méthodes existent également, basée sur le calcul de la probabilité '''a priori''' de chaque document d'appartenir à un cluster défini et reposant sur une analyse baysienne. | |||
Ces algorithmes souvent basés sur les méthodes de maximisation de l'espérance mathématique ([http://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm EM-algorithm]) et fonctionnent bien quand les données sont proches d'une loi normale (loi de Gauss). | |||
En général on peut reconnaître un tel algorithme par la représentation des résultats qui montre des "nuages" de points en ellipse : | |||
[[Image:avg-linkage.svg|thumb|none|250px | Cluster graph (algorithme EM) - source [https://www.flickr.com/photos/rosenfeldmedia/3344374190/ flikr]]] | |||
* Pour plus d'informations, voir [http://www.charuaggarwal.net/text-cluster.pdf Aggarwal et Zhai (2012, ch 5)]. | |||
== Références == | == Références == | ||
| Ligne 28 : | Ligne 262 : | ||
* Pons, P. & Latapy, M. (2005) Computing communities in large networks using random walks [http://arxiv.org/pdf/physics/0512106v1.pdf PDF] | * Pons, P. & Latapy, M. (2005) Computing communities in large networks using random walks [http://arxiv.org/pdf/physics/0512106v1.pdf PDF] | ||
* Chen and Lynch (1992). Automatic construction of networks of concepts characterizing document databases. IEEE ''Transactions on Systems, Man and Cybernetics, 22''(5):885–902. | |||
=== Manuel R === | === Manuel R === | ||
| Ligne 33 : | Ligne 269 : | ||
* [http://stat.ethz.ch/R-manual/R-patched/library/stats/html/hclust.html hclust : Hierarchical Clustering] | * [http://stat.ethz.ch/R-manual/R-patched/library/stats/html/hclust.html hclust : Hierarchical Clustering] | ||
*[http://cran.r-project.org/web/packages/cluster/cluster.pdf paquetage cluster sur cran.r-project.org] | |||
* Beloshytski, A. [http://fr.slideshare.net/whitish/textmining-with-r TextMining with R] | |||
* Timothy D'Auria [https://www.youtube.com/watch?v=j1V2McKbkLo Tutoriel complet pour effectuer une classification par machine learning] | |||
=== Références informelles === | === Références informelles === | ||
* Zong J. (2013) [http://jonathanzong.com/blog/2013/02/02/k-means-clustering-with-tfidf-weights K Means Clustering with Tf-idf Weights] | |||
* | |||
* Ryciak, N. [http://www.rexamine.com/2014/06/text-mining-in-r-automatic-categorization-of-wikipedia-articles/ Text mining in R – Automatic categorization of Wikipedia articles] | * Ryciak, N. [http://www.rexamine.com/2014/06/text-mining-in-r-automatic-categorization-of-wikipedia-articles/ Text mining in R – Automatic categorization of Wikipedia articles] | ||
| Ligne 47 : | Ligne 286 : | ||
* [http://en.wikipedia.org/wiki/Non-negative_matrix_factorization Wikipedia Non-negative Matrix Factorisation] | * [http://en.wikipedia.org/wiki/Non-negative_matrix_factorization Wikipedia Non-negative Matrix Factorisation] | ||
* [http://en.wikipedia.org/wiki/Latent_semantic_indexing Wikipedia Latent Semantic Indexing] | |||
* [http://en.wikipedia.org/wiki/Cosine_similarity Wikipedia Cosine similarity] | |||
* [http://youtu.be/2Znairz-hvU?t=8m4s Analyse de classification et de prédiction pour l'attribution de discours présidentiel à Obama ou à Ronney par Timothy D'Auria] | |||
[[Catégorie:Analytique et exploration de données]] | |||
Dernière version du 28 janvier 2015 à 21:12
| Analytique et exploration de données | |
|---|---|
| Module: Text mining | |
| ⚐ à finaliser | ☸ intermédiaire |
| ⚒ 2015/01/28 | |
| Voir aussi | |
| Catégorie: Analytique et exploration de données | |
Le Clustering
Le partitionnement de données (data clustering en anglais) est une des méthodes statistiques d'analyse des données. Elle vise à diviser un ensemble de données en différents « paquets » homogènes, en ce sens que les données de chaque sous-ensemble partagent des caractéristiques communes, qui correspondent le plus souvent à des critères de proximité (similarité). (source: Wikipedia). En clair, le clustering cherche à faire des classes telle que
- les différences intra-classe soient minimales pour obtenir des clusters
- les différences inter-classe soient maximales afin d'obtenir des sous-ensembles bien différenciés.
Dans le cas d'un corpus textuel, en général les données sont un ensemble de documents, pour lesquels on utilise un ensemble de termes pour les classer.
Le résultat d'une classification prends traditionnellement soit la forme d'un graphique de points ou d'un dendogramme
Cluster graph (algorithme EM) - source flikr
Cluster graph (k-means) - source wikimedia
Dendogram (classification hiérarchique) - source wikimedia
Définition d'une distance
Dans la plus part des cas, le calcul de la distance entre les documents se base sur la matrice termes-documents qui recense le nombre ou la fréquence d'apartition des termes dans chaque document du corpus. Voir la page Text mining pour un survol.
Distance du cosinus
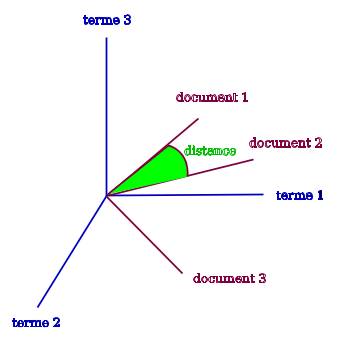
La distance la plus couramment utilisée est la distance du cosinus ou cosine qui est définie comme où dénote le produit scalaire et la norme associée.
Dans la norme euclidienne, cela s'écrit
où représente le nombre d'occurrences du terme k dans le document i (tirés par exemple de la matrice termes-documents).
Cosine généralisée
On peut généraliser la mesure du cosinus en introduisant une fonction de "damping" qui aura pour effet de rendre plus clair les différences (parfois minimes) entre les documents. Par exemple, souvent on remplace et par le logarithme ou la racine carrée de la fréquence d'apparition du terme k. C'est-à-dire, si dénote le nombre totale d'occurrences du terme k dans l'ensemble du corpus, on remplace dans la formule par ou par (et de même pour ).
La distance du cosinus est toujours comprise entre -1 et +1 et peut être reliée intuitivement avec la notion de corrélation de la manière suivante :
- plus deux documents sont similaires et plus ils auront tendance à utiliser les mêmes termes. Les termes seront alors corrélés, ce qui se traduit géométriquement par être "colinéaires", c'est à dire par un angle faible entre eux et donc un cosinus proche de +1 ou -1 ;
- inversement, deux documents non similaires auront tendance a avoir des termes décorrélées. Autrement dit, ils seront "orthogonaux" géométriquement et leur cosinus sera proche de 0.
Limitations de la distance du cosinus
Cette distance est parmi les plus utilisées, cependant elle présente tout de même quelques limitations.
Une des limites de la distance du cosinus est qu'elle ne tient pas compte de la possibilité d'utiliser des synonymes lors de la rédaction du corpus. Si un texte n'utilise que le mot "chien" et un autre que le mot "canidé", leur distance sera considérée comme grande. Ce point peut être résolu en faisant appel à des modifications du corpus comme avec la méthode LSI.
Une limitation plus importante de cette méthode, comme mentionné par Senellart et Blondel est que le modèle mathématique sous-jacent repose sur l'hypothèse d'un espace orthogonal, ce qui implique les termes soient globalement répartis uniformément les uns par rapport aux autres dans le corpus, ce qui est rarement le cas puisque le corpus est en principe une collection de document partageant des caractéristiques communes (et donc des similarités).
Autres distances possibles
Il est également possible de définir d'autre distances comme
- la distance de cluster proposée par Chen et Lynch (1972) qui est une distance asymétrique (si i et similaire à j cela ne veut pas dire que j est similaire à i) et définie par
où désigne la norme de i, c'est-à-dire la somme du nombre d'occurrences de chaque termes k dans le document i.
- les mesures de Jaccard définies par
Par exemple, on peut définir une mesure qui soit le quotient du nombre de fois où i et j apparaissent dans la même phrase divisé par le nombre de fois où i et j apparaissent (ensemble ou non).
Autres bases possibles pour la classification
D'autres bases existent pour la classification que la définition d'une distance pour définir la similarité entre deux termes. On peut voir à ce sujet Aggarwal & Zhai qui distinguent
- la méthode LSI (Latent Semantic Indexing) qui cherche a grouper les termes synonymes avant la classification. A ce sujet, voir Senellart & Blondel in Berry & Castellanos (2007), p25
- la méthode NMF (Non-negative Matrix Factorisation) dont le but est d'extraire de la matrice termes-documents un ensemble plus restreint de caractéristiques sur lesquelles seront appliqué la classification.
- les méthodes basées sur l'entropie
ou encore Pons & Latapy au sujet des marches aléatoires.
Principe général
Le principe général est de regrouper les documents par similarité afin de dégager des classes qui soit au maximum
- homogènes, c'est-à-dire dont les éléments soient similaires entre eux ;
- différenciées, c'est-à-dire que les éléments de classes différentes soient non similaires (en tout cas moins similaires que les éléments internes à leur classe).
Pour ce faire, il existe plusieurs stratégies, chacune avec avantages et inconvénients.
Regroupement Hiérarchique
Le concept de base du regroupement hiérarchique est de fusionner successivement les documents en clusters (groupes) puis les clusters entre eux selon leur degré de similarité. Elle se décompose donc en deux étapes répétées en boucle (jusqu'à ce qu'il ne reste qu'un seul cluster unique) :
- calculer la similarité (distance) entre tous les cluster existant à l'étape en cours ;
- fusionner les deux clusters qui sont les plus similaires.
Présentation des résultats
Les résultats du regroupement sont en général présentés sous forme de dendogram :
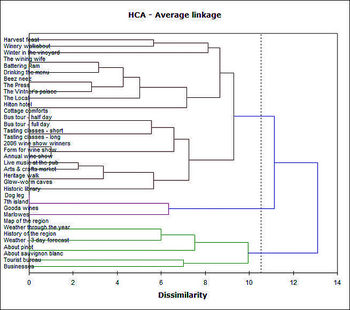
- sur un axe de coordonnées les documents analysés (ici en vertical) ;
- sur l'autre le degré de similarité (ici en horizontal) ;
- chaque document et cluster est représenté par une ligne (ici horizontale) ;
- lorsque deux lignes sont reliées, c'est que les documents (ou les clusters) correspondant sont fusionnés dans un nouveau cluster.
Plus la ligne horizontale est courte et plus les clusters sont similaires. Cela permet d'avoir une visualisation claire des liens et similitudes entre les éléments.
Remarque : cette représentation n'est pas limitée à l'analyse de texte et se trouve très souvent utilisée, notamment en génétique et biologie pour représenter le degré de similitudes entre les espèces (arbre phylogénétique).
Choix de méthode de regroupement hiérarchique
La difficulté revient alors a bien choisir la façon de calculer le degré de similitude entre deux clusters. Par exemple, on peut choisir soit le meilleur cas possible, le pire cas possible ou une forme de moyenne. En général, il s'agit de choisir un ou plusieurs représentants du groupe (cluster) et de calculer la similarité en se basant sur ces représentants. Pour une visualisation graphique des méthode de classement, voir cette page.
Single linkage
La méthode du single linkage correspond au choix du "meilleur des cas". Dans cette méthode, on choisit comme représentant du groupe le document qui est le plus similaire avec les documents de l'autre groupe. Ainsi la similarité entre les cluster est le maximum de la similarité entre les documents des clusters.
Le problème principal de cette méthode est que cela peut créer un effet de "chaîne" qui finira par regrouper des éléments qui ne sont pas similaires entre eux. Si A et B sont similaires et B et C sont similiaire, cela ne veut pas dire que A et C sont similaire. Par exemple, un texte sur la voltige à cheval peut être similaire à un texte sur les chevaux de courses lui-même similaire à un texte sur les courses de vélo qui pourra être similaire à un texte sur l'utilisation du vélo en milieu urbain...
Complete linkage
La méthode du complete linkage est l'opposée du single linkage et correspond au choix du "pire des cas". Dans cette méthode, on choisit comme représentant du groupe le document qui est le moins similaire avec les documents de l'autre groupe. Ainsi la similarité entre les cluster est le minimum de la similarité entre les documents des clusters.
Cette méthode permet d'éviter l'effet de "chaîne" mais en contrepartie est très conservatrice et crée souvent des dendogrammes très alongés (car attribue facilement des similarités faibles). De plus, elle demande un grande puissance de calcul car elle nécessite un grand nombre de comparaisons à chaque étape de calcul pour déterminer la paire la moins similaire.
Average linkage
Le méthode de l'average linkage est une méthode intermédiaire qui détermine une moyenne (average en anglais) entre les documents des clusters. Dans cette méthode, on choisit comme similiarité la moyenne des similarités entre toutes les paires d'éléments des clusters considérés. Ainsi la similarité entre les cluster est la moyenne de la similarité entre les documents des clusters.
Tout comme la méthode du complete linkage, l'average linkage permet d'éviter l'effet de "chaîne" et de plus, fournit des clusters qui sont souvent de qualité car homogènes (les influences des éléments "extrêmes" se contrebalancent lors de la prise de la moyenne). En revanche, cette méthode nécessite également une puissance de calcul accrue car il faut considérer toutes les paires possibles lors de chaque étapes de calcul. Pour contourner ce problème on peut ne considérer que le document "moyen" de chaque cluster dans le calcul (et actualiser le choix du document moyen à chaque étape). Cela ne fonctionne pas avec tout les types de les jeux de données (il faut une certaine homogénéité intrinsèque du corpus) mais semble fonctionner particulièrement bien dans le cas de données textuelles (cf . Aggarwal & Zhai, 2012). C'est donc une méthode robuste et qui fonctionne particulièrement bien dans le cadre du text mining.
Exemple
Pour un bon exemple d'application de la classification hiérarchique, cette fois au sujet des termes les plus utilisés dans les oeuvres de Shakespeare, on peut voir les deux posts suivants de Andrew Collier :
- Text mining the complete work of William Shakespeare (avec code sous R, en anglais)
- Clustering the Words of William Shakespeare (avec code R et package "cluster", en anglais)
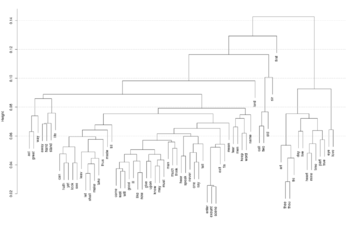
Par exemple, sur le dendograme issu de son analyse, il remarque que le termes "enter", "exeunt" et "scene" vont ensemble, ce qui est certainement du au fait que le découpage traditionnel des scènes de théâtre suit l'entrée (enter) et la sortie (exeunt) des personnages. Nous pouvons également remarquer que "eye" et "love" vont de pair, ainsi que "fear" et "men" ou "keep" et "word", ce qui peut nous conduire a formuler des hypothèses sur le status de la promesse chez Shakespeare (surtout quand on considère les pièces historiques où les trahisons sont légions). De manière plus macroscopique, on peut également analyser le fait que les termes relatifs à l'amour et aux sentiments forment une classe "à part" clairement séparée du reste des termes du corpus.
Résumé de la méthode sous R
En partant de la matrice de terme-document et de la distance associée
DTM <- DocumentTermMatrix(doc.corpus) TDM.dist = dist(TDM.scaled)
on peut utiliser la fonction "agnes" du paquetage "cluster" (dont la documentation peut être trouvée sur cran.r-project.org) pour calculer le dendogramme
library(cluster) ag.result <- agnes(x = TDM.dist, method = "complete")
et l'afficher avec
plot(ag.result, which.plots = 2, main = "", sub = "", xlab = "")
On peut aussi regarder cette vidéo youtube (en anglais) qui présente le Clustering hiérarchique sous R pour 4 villes.
Regroupement basés sur la distance
Le regroupement basé sur la distance est un ensemble de méthodes dont le but est de réduire le corpus à un nombre de cluster fixés à l'avance. Il s'agit donc plus de méthodes de partitionnement du corpus. Bien entendu, puisque le nombre de cluster est fixé à l'avance, il s'agit de bien le choisir. Heureusement les algorithmes utilisés sont souvent rapides et permettent de "tester" plusieurs nombre de clusters pour déterminer le meilleur.
L'algorithme conne également les équations des droites de différenciation, ce qui permet également de classifier un nouveau document facilement.
Présentation des résultats
Les résultats sont souvent présentés sous forme de nuage de points comprenant souvent le tracé des lignes "limites" de démarcation entre les clusters.
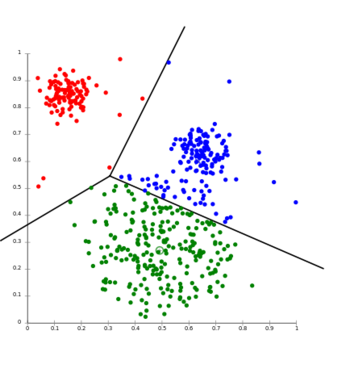
Notons que les lignes noires définissent les zones d'attribution à chaque cluster (aussi appelée partition de Voronoi) et permettent ainsi la classification immédiate d'un document inconnu (il suffit de regarder dans quelle zone il "tombe").
k-medoid
La méthode k-medoid utilise comme point de départ, pour créer les clusters, un ensemble de documents issus du corpus (appelés medoids ou ancres) et construit les groupes autour. Dans la phase d'initialisation, chaque document est assigné au medoid qui lui est le plus proche (la plus similaire). Il s'ensuit alors un processus itératif où la distance moyenne entre les document et le medoid de leur cluster est minimisée, conduisant ainsi à un meilleur regroupement des documents entre eux.
Une itération se décompose en trois étapes :
- On choisit un medoid au hasard et on le remplace par un document choisi au hasard dans le corpus ;
- On recalcule les clusters avec le nouveau medoid et on compare la nouvelle distance moyenne avec l'ancienne distance moyenne ;
- si la nouvelle distance moyenne est meilleure (i.e. plus petite) on conserve le nouveau medoid.
Le processus est alors itéré jusqu'à ce qu'aucune nouvelle substitution n'améliore la classification.
Un inconvénient de cette méthode est sa lenteur de convergence, il faut en général de très nombreuses substitution pour atteindre l'optimum. De plus, un inconvénient majeur est que cette méthode ne fonctionne pas très bien avec les données textuelles (cf. Aggarwal & Zhai, 2012). En effet, comme le medoid est un document issus du corpus, il ne contient en général pas tout les termes utiles à une classification efficace de la plus part des autres documents (qui auront en général peu de termes communs avec les medoids choisis) car "un document medoid ne contient souvent pas à lui seul tout les concepts requis pour construire un cluster efficacement" ( Aggarwal & Zhai (2012), notre traduction).
k-mean
Basée sur le même type de modèle, la méthode k-means utilise également un ensemble de k représentants (appelées graines ou seeds) autour desquels les clusters sont construits. Cependant dans ce cas les représentants ne sont pas forcément choisis parmis le corpus mais les graines sont fabriquées et recalculées à chaque étape. En fait, il s'agit de "documents fictifs" contenant une liste de termes avec le "bon" nombre d'occurrences.
En pratique les graines initiales sont souvent choisies parmis les documents du corpus puis les documents sont assignés aux clusters de la graines la plus proche. Lors de l'itération suivante, les graines sont remplacées par le centroid (calculé) du cluster.
La nouvelle graine est ainsi un document fictif qui contiendrait chacun des termes existant dans une proportion correspondant à la moyenne de la fréquence d'apparition du terme dans le cluster. Par exemple, si un terme apparaît 35 fois dans un cluster de 10 documents alors il apparaîtra (fictivement) 3.5 fois dans la graine.
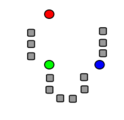
- Démonstration d'une itération - source wikipedia :
2) Les k clusters sont construits autour des graines (ici avec la [partition de Voronoi] correspondante).
- Pour un exemple d'algorithme k-means, voir le blog de Jonathan Zong
Une des grandes qualités de la méthode k-means est qu'elle converge extrêmement vite, en 5 itérations environ. Un des inconvénient majeur est qu'elle reste dépendante du choix des graines initiales. Un autre inconvénient est que le centroid calculé (qui sert de nouvelle graine) a tendance à contenir un très grand nombre de termes. En effet il contient l'ensemble de tout les termes qui ont à un moment donné fait partie des documents se trouvant dans le cluster, parfois en très petite proportion, ce qui ralenti beaucoup les calculs. Certaines méthodes existent cependant pour palier à ce problème, comme les méthodes Scatter-Gather ci-dessous.
Exemples sous R
De nombreux exemples sous R sont disponibles en vidéos, notamment sur youtube par Timothy D'Auria :
- Analyse de classification et de prédiction pour l'attribution de discours présidentiel à Obama ou à Ronney
- Tutoriel complet pour effectuer une classification par machine learning
Autres méthodes
Méthodes hybrides : Eclater et regrouper (Scatter-Gather)
D'autres méthodes existent dont la mise en oeuvre peut être plus complexe comme
- le Buckshot qui cherche à améliorer les algorithmes de type k-means en sélectionnant graines au lieu de k puis les fusionnent en k graines ;
- la Fractionalisation qui répartit le corpus en sous-corpus de tailles réduites, réalise une agglomération des corpus pour en réduire le nombre puis classifie le corpus réduit.
Méthodes basées sur la fréquence des termes
D'autres méthodes existent encore, basées entre autres sur la fréquence de présence des termes dans les documents.
Pour de plus amples informations sur ces méthodes, voir Aggarwal et Zhai (2012)
Méthodes probabilistes
D'autres méthodes existent également, basée sur le calcul de la probabilité a priori de chaque document d'appartenir à un cluster défini et reposant sur une analyse baysienne. Ces algorithmes souvent basés sur les méthodes de maximisation de l'espérance mathématique (EM-algorithm) et fonctionnent bien quand les données sont proches d'une loi normale (loi de Gauss).
En général on peut reconnaître un tel algorithme par la représentation des résultats qui montre des "nuages" de points en ellipse :
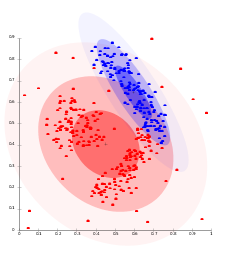
- Pour plus d'informations, voir Aggarwal et Zhai (2012, ch 5).
Références
- Berry, M. & Castellanos, M. (2007) Survey of Text Mining: Clustering, Classification, and Retrieval, Second Edition PDF
- Aggarwal, C. & Zhai C. (2012). A Survey of Clustering Algorithms, in Mining Text Data, Springer. ch4 PDF
- Grivel, L. (s.d.) Outils de classification et de catégorisation pour la fouille de textes. http://www.irit.fr/SDC2006/cdrom/contributions/Grivel-isko-sdc.pdf PDF]
- Feinerer, I., Hornik, K. & Meyer, D. (2008). Text Mining Infrastructure in R. Journal of Statistical Software, 25. PDF
- Pons, P. & Latapy, M. (2005) Computing communities in large networks using random walks PDF
- Chen and Lynch (1992). Automatic construction of networks of concepts characterizing document databases. IEEE Transactions on Systems, Man and Cybernetics, 22(5):885–902.
Manuel R
- hclust : Hierarchical Clustering
- paquetage cluster sur cran.r-project.org
- Beloshytski, A. TextMining with R
Références informelles
- Zong J. (2013) K Means Clustering with Tf-idf Weights













![2) Les k clusters sont construits autour des graines (ici avec la [partition de Voronoi] correspondante).](/fmediawiki/images/thumb/c/c6/K_Means_Example_Step_2.png/139px-K_Means_Example_Step_2.png)