Méthodes de classification en text mining
| Analytique et exploration de données | |
|---|---|
| Module: Text mining | |
| ⚐ à finaliser | ☸ intermédiaire |
| ⚒ 2014/12/18 | |
| Voir aussi | |
| Catégorie: Analytique et exploration de données | |
A l'inverse de la classification où les catégories n'étaient pas connues par avance, la classification essaie de classer les documents du corpus dans un certain nombre de catégories prédéfinies. De plus, cette une méthode entraînée, c'est-à-dire qu'elle nécessite un ensemble de documents "représentatifs" des catégories choisies. Elle peut se rapprocher d'une analyse de thématique "Topic modelling", mais, à l'inverse de ce dernier, elle ne permet pas l'attribution de plusieurs catégorie à un même document. Un exemple concret de catégorisation serait de différencier le emails de spam (pourriels) des emails légitimes.
Généralités
Ces méthodes sont extrêmement générales car elles sont basées sur l'analyse d'un réseau (graph) ou de nuages de points dans un espace vectoriel. En fait, a partir du moment où l'on peut représenter les données sous formes de dimensions chiffrées ou si l'on a une notion de distance (chiffrée) entre les items, on peut utiliser ces méthodes pour l'analyse des items.
Préparation du corpus
Ces méthodes demandent la préparation habituelle du corpus, stop-words, lemmatisation et construction de la matrice terme-document (voir Text mining).
Elles reposent sur plusieurs hypothèses, les plus essentielles étant :
- Les catégories constituent une base ou un corpus d'apprentissage (pour l'algorithme)
- Les documents présentés pour être classés sont représentés par des vecteurs de termes pondérés (ceci est tiré de la matrice terme-documents qui compte le nombre d'occurrences de chaque terme dans chaque document). En clair, chaque document est représenté par une liste de mots-clés avec la fréquence d'occurrence du mot dans le document).
- Pour pondérer les occurrences des mots, on a souvent recours à la méthode TfIdf, qui améliore les contraste entre les documents par un passage au logarithme.
- où désigne le poids du mot i dans le document j, la fréquence du mot i dans le document j (tirée de la matrice terme-document), N le nombre de documents considérés et le nombre total d'occurrence du mot i dans l'ensemble des documents.
- Notons enfin que ces méthodes reposent sur le choix d'une distance entre document, comme par exemple la distance du cosinus (voir aussi Clustering).
Catégorisation linéaire Rocchio
Cette méthode est la plus simple. Elle classe un document dans la catégorie dont il est le plus proche du barycentre (selon la distance que l'on a choisie, voir plus haut la distance du cosinus).
Phase d'apprentissage
Cette méthode est basée sur une phase d'apprentissage, où certains documents servent à établir une base contre laquelle les autres documents seront classés. Un ensemble de documents bien choisi est donc fourni au départ comme représentatif des catégories voulues.
Algorithme de la méthode
- On commence par construire des vecteurs "de base" des catégories considérées. En clair il s'agit pour chaque catégorie d'avoir un vecteur pondéré associant à chaque mot clé son poids dans la catégorie (ex: si on a comme catégorie "animaux" et "lieu", alors "chien" aura un poids fort dans "animaux" et faible dans "lieux", "Paris" aura un poids fort dans "lieux", alors que "chenil" pourra avoir un poids moyen dans les deux).
- Le vecteur de base de la catégorie k se calcule comme suit :
- Pour chaque mot clé on tire de la matrice terme-document pondérée l'ensemble de ces poids dans les documents de la catégorie k.
- On calcule le poids du mot dans la catégorie k en faisant la différence entre la moyenne des poids du mot dans les documents appartenant à la catégorie k et la moyenne du poids du mot dans les documents n'appartenant pas à la catégorie k.
- On obtient ainsi un ensemble de vecteurs de poids pour chaque catégorie (vecteurs de barycentres).
- Pour chaque document à classer, il suffit de calculer la distance avec chacun des vecteurs "de base" et d'associer le document à la catégorie dont il est le plus proche.
Dans l'exemple ci-dessous, les catégorie sont représentées en bleu et le document à classer en vert.
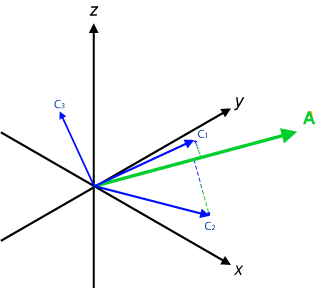
Le document A en vert va être classé avec la catégorie car c'est la plus proche, mais il aurait peut-être pu également appartenir à la catégorie . Ce problème peut être éviter en faisant appel à des techniques d'analyse de thèmatique Topic modelling.
Catégorisation par les K plus proches voisins
Dans cette méthode, on classe un document dans la même catégorie que la majorité (pondérée) de ses K plus proches voisins (selon la distance que l'on a choisie, voir plus haut la distance du cosinus).
Phase d'entraînement
Cette méthode est basée sur des instances (ou exemples) de document de chaque catégorie. Ainsi, comme pour la catégorisation linéaire, plus on fourni d'exemples en phase d'entraînement, meilleur sera le résultat. Un ensemble de documents bien choisidoit donc être fourni au départ comme représentatif des catégories voulues.
Algorithme de la méthode
A la différence de la catégorisation linéaire, aucune phase préliminaire n'est requise. Les étapes se déroulent comme suit :
- Calculer quels sont les K documents les plus proches (K plus proches voisins selon la distance choisie), ainsi que leur catégorie d'appartenance
- Affecter le document courant à la catégorie qui avait le plus de représentant parmi les K plus proches voisins (système de vote)
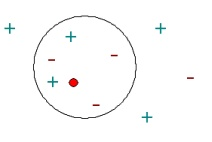
Ici, pour K=1 le document (point rouge) est classé avec les "+" mais pour K=5 il serait classé avec les "-". Ainsi le choix de K est très important.
Choix de K
Pour éviter les problèmes d'égalité, pour les tâches de classification en deux catégories, on utilise uniquement des valeurs de K impaires.
De plus, un valeur trop petite va donner trop d'importance aux petites variations "aléatoires" ou "bruit" des documents. Une valeur trop grande va être d'une part lourde en calcul et d'autre part risque de créer des catégories trop petites (avec pas assez de documents dedans).
En général
- on teste plusieurs valeurs de K
- on vérifie les résultats par de la Cross-validation
Un bonne valeur de départ est en général où n est le nombre de documents (cf. Thirumuruganathan, 2010).
Mathématiquement, le nombre optimal serait entre et où C est une constante déterminée en fonction du corpus. (cf. Maier, Hein, Luxburg, 2009).
Tester le choix de K: Cross-validation
La cross-validation consiste a comparer les catégorisations déterminées par plusieurs ensemble de documents "d'entraînement" (ensemble de mêmes tailles). La plus simple consiste a créer 2 ensembles aléatoires de documents ( et , de meme taille) puis
- entraîner sur et classer
- entraîner sur et classer
- comparer les deux catégorisations, en général par regression linéaire et calcul de la Moyenne de l'Ecart-Type de l'Erreur (MSE)
Prise en compte de la distance effective
Dans la version simple que nous venons de voir, seul le nombre de voisins dans chaque catégorie était pris en compte, indépendamment de la distance avec le document courant. Cependant, il est sensé de donner plus de poids aux documents les plus proches qu'au plus éloignés. Pour remédier à cela, on utilise en général une pondération exponentielle (issue de la même idée que la pondération en logarithme de la matrice terme-document). On calcule la moyenne pondérée des distances entre le document courant et ses plus proches voisins
où désigne la distance entre le document et et la fonction exponentielle.
Limitations : la malédiction des dimensions
Un des problèmes fondamentaux de cette méthode, comme de toutes les méthodes se basant sur une distance vectorielle, est ce que l'on appelle la malédiction des dimensions.
- En effet, en général le nombre de termes différents considérés pour calculer la distance est très grand (et donc la dimension de la matrice terme-document est très grande).
Le problème dans ce cas est que la matrice terme-document contiendra beaucoup de valeurs très faibles voire nulle (on parle alors de matrice creuse).
- Par conséquent la distance entre les documents sera en général très petite et le nombre de termes vraiment utiles à la classification très faible (en proportion du total des termes).
- Il en résultera un manque de précision dans la classification car l'algorithme prendra en compte de nombreux paramètres qui ont peu d'impact.
Remédiations possibles
Pour remédier à cela de nombreuses méthodes existent (voir par exemple Radovanovic et Ivanovic (2008) ou slides Deokar (2009)). Entres autres, on peut citer
- la méthode KNN avec poids ;
- l'application de "noyaux" ou "kernels" à la matrice par multiplication matricelle ;
- la mise à l'echelle multidimensionelle (multidimensional scalling, MDS) qui projette la matrice sur un espace de dimension réduites ;
- l'analyse en composantes principales ;
- l'analyse de discriminant (voir Berry et Castellanos (2007))
Elimination rétrograde
Une méthode classique et simple pour résoudre le problème des dimensions est l'élimination rétrograde de terme dans les documents exemples :
Pour chaque termes considérés
- Effacer le termes dans les documents exemples (c'est-à-dire ne pas considérer ce terme lors du calcul de la distance)
- Puis, pour chaque document exemple :
- déterminer les K plus proches voisins parmi les documents exemples ;
- prédire la catégorie d'appartenance de selon l'algorithme du K plus proche voisin
- Calculer la qualité des prédictions comme le quotient entre le nombre de documents exemples bien classés et le nombre total de documents exemples.
- Si la qualité est plus faible qu'avant, rétablir le terme effacé, sinon le laissé effacé
Continuer avec le terme suivant
k-nearest neighbors avec R
Il est possible d'implémenter cet algorithme sous R avec la fonction "knn" (voir Feinerer, Hornik et Meyer (2008) et knn.html). La syntaxe générale étant
knn(train, test, cl, k = 1, l = 0, prob = FALSE, use.all = TRUE)
Pour aller plus loin
Ces méthodes sont tirées de la branche de l'informatique "machine learning" car elles font appel à des phases d'entraînement et d'apprentissage de la part del'algorithme.
D'autres approchent sont également possible, par exemple
- Les réseaux de neurones où l'algorithme utilise les données fournies après la phase d'apprentissage et une boucle de feedback pour continuer à apprendre et améliorer les prédictions futures.
- Les méthodes probabilistes basées sur un calcul des probabilités de classement a priori et a posteriori, et qui se rapprochent des méthodes d'analyse de thématiques.
- Les méthodes probabilistes basées sur des marches aléatoires sur le graphe d'adjacence des documents (un reseau "hypertexte" où deux documents du corpus seraient d'autant plus liés qu'ils sont proches selon la distance choisie). Ces algorithmes peuvent être rapprochés du fameux "Pagerank" utilisé par Google pour déterminé les résultats des recherches. (voir Pons et Latapy (2005) et Tellier s.d.)
Références
- Berry, M. & Castellanos, M. (2007) Survey of Text Mining: Clustering, Classification, and Retrieval, Second Edition PDF
- Brown, S. (s.d.) K nearest neighbor ([www.cs.uvm.edu/~xwu/kdd/kNN-11.ppt support de cours ppt])
- Deokar, S (2009). Weighted K Nearest Neighbor. (slides pdf)
- Ghosh, S, Roy, S et Bandyopadhyay, S. (2012). A tutorial review on Text Mining Algorithms. International Journal of Advanced Research in Computer and Communication Engineering, 1(4) (pdf)
- Grivel, L. (s.d.) Outils de classification et de catégorisation pour la fouille de textes (pdf)
- Gupta, V. et Lehal, G. (2009) A Survey of Text Mining Techniques and Applications. Journal of Emerging Technologies in Web Intelligence, 1(1) (pdf)
- Grimal, C. et Bisson, G. (s.d.) Amélioration de la co-similarité pour la classification de documents (pdf)
- Maier, M., Hein, M. Luxburg, B. (2009). Optimal construction of k-nearest neighbor graphs for identifying noisy clusters PDF
- Pons, P. & Latapy, M. (2005) Computing communities in large networks using random walks PDF
- Radovanovic, M. et Ivanovic, M. (2008) Text Mining: approaches and applications. Novi Sad Journal of Mathematics, 38(3). (pdf)
- Tellier, I. (s.d.) Introduction à la fouille de textes. (pdf)
Références R
- Feinerer, I. Hornik, K et Meyer, D. (2008) Text mining infrastructures in R (pdf)
- Knn tutorial for R : knn.html
Autres références
- Thirumuruganathan, S. (2010). A Detailed Introduction to K-Nearest Neighbor (KNN) Algorithm Blog Entry
- Page Wikipedia TfIdf