« STIC:STIC III (2018)/Brodeuse phi » : différence entre les versions
| (10 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{tutoriel | |||
|fait_partie_du_cours=Physicalisation de données | |||
|fait_partie_du_module=STIC:STIC III (2018)/Prototypes de physicalisation - broderie machine | |||
|pas_afficher_sous-page=Non | |||
|statut=à finaliser | |||
|difficulté=débutant | |||
|cat tutoriel=Physicalisation de données | |||
}} | |||
== Physicalisation du nombre d'or par la brodeuse == | == Physicalisation du nombre d'or par la brodeuse == | ||
Le prototype proposé est une physicalisation par la brodeuse du nombre d'or. | |||
== Description == | |||
Considéré comme la proportion parfaite en architecture ou en art, le nombre d'or se retrouve aussi dans dans certain phénomène naturel comme la répartition des étamines sur la fleur de tournesol. | Considéré comme la proportion parfaite en architecture ou en art, le nombre d'or se retrouve aussi dans dans certain phénomène naturel comme la répartition des étamines sur la fleur de tournesol. | ||
Le nombre d'or '''φ''' se définit comme l'unique solution positive de l'équation | Le nombre d'or '''φ''' se définit comme l'unique solution positive de l'équation | ||
<math>x^2-x-1=0</math> | |||
===== Suite de Fibonnaci ===== | ===== Suite de Fibonnaci ===== | ||
La suite de Fibonacci est une suite d'entiers où chaque terme est égale à la somme des deux termes précédents, les deux premiers termes étant égaux à 1. | La suite de Fibonacci est une suite d'entiers où chaque terme est égale à la somme des deux termes précédents, les deux premiers termes étant égaux à 1. | ||
<math>\forall n>0, F_0=1 , F_1=1, F(n)= F(n-1)+F(n-2)</math> | |||
Si F(n) désigne le nième terme de la suite de Fibonacci et F(n-1) le n-1 ème terme de la suite, alors | |||
<math>\textstyle \lim_{n \to \infty} \displaystyle F(n)/F(n-1) =\phi</math> | |||
===== Géométrie et Spirale d'or ===== | ===== Géométrie et Spirale d'or ===== | ||
| Ligne 24 : | Ligne 37 : | ||
Dès lors le rapport r(n)/r(n-1) tend vers φ pour n grand et les côtés r(n) et r(n-1) forment un rectangle d'or. | Dès lors le rapport r(n)/r(n-1) tend vers φ pour n grand et les côtés r(n) et r(n-1) forment un rectangle d'or. | ||
== Objectif == | |||
Beaucoup de propriétés mathématiques ont été découvertes par la géométrie avant le développement des ordinateurs. La construction d'une spirale d'or est une solution élégante pour approcher le nombre φ qui est irrationnel. | Beaucoup de propriétés mathématiques ont été découvertes par la géométrie avant le développement des ordinateurs. La construction d'une spirale d'or est une solution élégante pour approcher le nombre φ qui est irrationnel. | ||
La brodeuse devient ainsi un outil optimal pour représenter physiquement le nombre d'or via la spirale et les rectangles d'or. | La brodeuse devient ainsi un outil optimal pour représenter physiquement le nombre d'or via la spirale et les rectangles d'or. | ||
=== Représentation physique == | == Modélisation == | ||
La première phase a consisté à effectuer une modélistaion vectorielle sur Inkscape de la spirale d'or. | |||
Les disque sur Inkscape possède la propriété d'être diminué en arc de cercle ou en tranche de camembert. La construction de la spirale a été effectuée de la manière suivante: | |||
# Tracer un disque | |||
# Le réduire à un quart de disque | |||
# Faire plusieurs copier/coller du quart de disque. | |||
# Accoler deux quarts de disque pour former le demi disque de rayon 1. | |||
# Doubler le rayon d'un troisième quart de disque (Maj+Ctrl+M, puis sélectionner dimension, puis indiquer 200% dans longueur et cocher redimensionner proportionnellement) et l'accoler au demi-disque | |||
# Tripler le rayon d'un autre quart de disque et l'accoler au quart de disque de rayon 2 de sorte que l'arc de cercle se prolonge en spirale. | |||
# Sélectionner un autre quart de disque et quintupler son rayon. L'accoler au quart de disque de rayon 5 de sorte que l'arc de cercle se prolonge en spirale. | |||
# Répetez l'opération jusqu'à une taille satisfaisante de la spirale d'or. (La spirale brodée contenaient 6 quarts de disque). | |||
== Paramétrisation avec Inkstitch == | |||
Le premier prototype avait été paramétré avec Inkstitch avec une longueur de point de 2,5 [mm]. Puis envoyé à la brodeuse. Le résultat n'avait été guère probant, les coutures à l'intérieure des quarts de disque de la spirale étant très espacées. | |||
Les paramètres ont donc été modifié pour un espacement de crête à crête de 0.4 [mm] et une longueur de point de 1,5 [mm]. Puis l'image a té traité avec stitch era pour incorporer les caractères alphanumériques. | |||
== Représentation physique == | |||
La dernière phase a consisté à broder la spirale via la brodeuse. Si le résultat c'est avéré de bien meilleure qualité que le précédent surtout au niveau du remplissage des quarts de disque de la spirale, la densité des points a été trop grande surtout au niveau de la partie centrale entraînant des pliures du tissu. | |||
Si un troisième prototype devait être produit, une longueur de point de 2,0 [mm] devrait suffire. | |||
<gallery mode="packed" heights="200px"> | |||
<gallery> | |||
Fichier:Phi.svg|alt=La spirale d'or|La spirale d'or | Fichier:Phi.svg|alt=La spirale d'or|La spirale d'or | ||
Fichier:Spirale d'or inkscape.png|alt=la spirale d'or modélisée avec inkscape.|la spirale d'or modélisée avec inkscape. | Fichier:Spirale d'or inkscape.png|alt=la spirale d'or modélisée avec inkscape.|la spirale d'or modélisée avec inkscape. | ||
Dernière version du 7 janvier 2020 à 11:34
| Physicalisation de données | |
|---|---|
| Module: STIC:STIC III (2018)/Prototypes de physicalisation - broderie machine | |
| ⚐ à finaliser | ☸ débutant |
| ⚒ 2020/01/07 | |
Physicalisation du nombre d'or par la brodeuse
Le prototype proposé est une physicalisation par la brodeuse du nombre d'or.
Description
Considéré comme la proportion parfaite en architecture ou en art, le nombre d'or se retrouve aussi dans dans certain phénomène naturel comme la répartition des étamines sur la fleur de tournesol.
Le nombre d'or φ se définit comme l'unique solution positive de l'équation
Suite de Fibonnaci
La suite de Fibonacci est une suite d'entiers où chaque terme est égale à la somme des deux termes précédents, les deux premiers termes étant égaux à 1.
Si F(n) désigne le nième terme de la suite de Fibonacci et F(n-1) le n-1 ème terme de la suite, alors
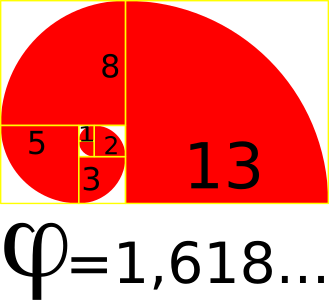
Géométrie et Spirale d'or
Du point de vue géométrique, soit deux longueur a et b (non-nulles) dont le rapport de a sur b est égal au rapport de a + b sur a. Le nombre d'or φ est alors la proportion a/b.
Les longueurs a et b représente un rectangle considéré parfait en art ou en architecture. Il est possible de construire une série de rectangle d'or par une spirale logarithmique particulière.
On trace un demi-cercle de rayon r. Puis d'une extrémité de l'arc de cercle, on continue à tracer un quart de cercle de rayon 2r. Puis à l'extrémité de l'arc de cercle, on trace un quart de cercle de rayon 3r,...., à la nième extrémité d'arc de cercle, on trace un quart de cercle de rayon égale à la somme des rayon des deux quarts de cercle précédents.
On retrouve ainsi la suite de Fibonacci où le rayon r(n)=r(n-1)+r(n-2).
Dès lors le rapport r(n)/r(n-1) tend vers φ pour n grand et les côtés r(n) et r(n-1) forment un rectangle d'or.
Objectif
Beaucoup de propriétés mathématiques ont été découvertes par la géométrie avant le développement des ordinateurs. La construction d'une spirale d'or est une solution élégante pour approcher le nombre φ qui est irrationnel.
La brodeuse devient ainsi un outil optimal pour représenter physiquement le nombre d'or via la spirale et les rectangles d'or.
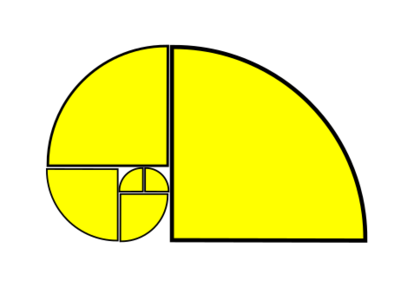
Modélisation
La première phase a consisté à effectuer une modélistaion vectorielle sur Inkscape de la spirale d'or.
Les disque sur Inkscape possède la propriété d'être diminué en arc de cercle ou en tranche de camembert. La construction de la spirale a été effectuée de la manière suivante:
- Tracer un disque
- Le réduire à un quart de disque
- Faire plusieurs copier/coller du quart de disque.
- Accoler deux quarts de disque pour former le demi disque de rayon 1.
- Doubler le rayon d'un troisième quart de disque (Maj+Ctrl+M, puis sélectionner dimension, puis indiquer 200% dans longueur et cocher redimensionner proportionnellement) et l'accoler au demi-disque
- Tripler le rayon d'un autre quart de disque et l'accoler au quart de disque de rayon 2 de sorte que l'arc de cercle se prolonge en spirale.
- Sélectionner un autre quart de disque et quintupler son rayon. L'accoler au quart de disque de rayon 5 de sorte que l'arc de cercle se prolonge en spirale.
- Répetez l'opération jusqu'à une taille satisfaisante de la spirale d'or. (La spirale brodée contenaient 6 quarts de disque).
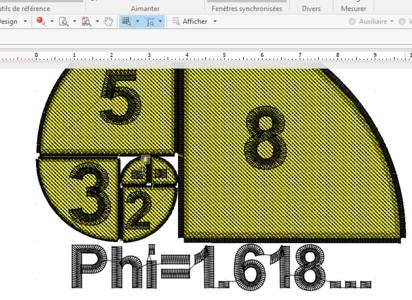
Paramétrisation avec Inkstitch
Le premier prototype avait été paramétré avec Inkstitch avec une longueur de point de 2,5 [mm]. Puis envoyé à la brodeuse. Le résultat n'avait été guère probant, les coutures à l'intérieure des quarts de disque de la spirale étant très espacées.
Les paramètres ont donc été modifié pour un espacement de crête à crête de 0.4 [mm] et une longueur de point de 1,5 [mm]. Puis l'image a té traité avec stitch era pour incorporer les caractères alphanumériques.
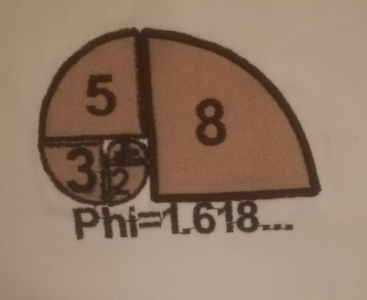
Représentation physique
La dernière phase a consisté à broder la spirale via la brodeuse. Si le résultat c'est avéré de bien meilleure qualité que le précédent surtout au niveau du remplissage des quarts de disque de la spirale, la densité des points a été trop grande surtout au niveau de la partie centrale entraînant des pliures du tissu.
Si un troisième prototype devait être produit, une longueur de point de 2,0 [mm] devrait suffire.