« Tutoriel OpenSCAD » : différence entre les versions
Aucun résumé des modifications |
|||
| Ligne 1 181 : | Ligne 1 181 : | ||
== Traduction imcomplète - Suite à traduire == | == Traduction imcomplète - Suite à traduire == | ||
[[Catégorie: Impression 3D]] | |||
Version du 4 novembre 2015 à 11:43
- Ce tutoriel est une traduction (mise à jour) de ce tutoriel : http://edutechwiki.unige.ch/en/OpenScad_beginners_tutorial
- Attention, il se base sur la version "2015.03" , certaines choses sont donc sujettes à ne plus correspondre avec de prochaines versions
Introduction
"OpenSCAD est un logiciel pour créer des objets CAD solides 3D. C'est un logiciel gratuit et disponible pour Linux / UNIX, MS Windows et Apples OS X. Contrairement à la plupart des logiciels libres pour créer des modèles 3D (comme Blender), il ne se concentre pas sur les aspects artistiques de la modélisation 3D, mais plutôt sur les aspects CAD. Ainsi, il pourrait être le logiciel à envisager pour créer des modèles 3D de pièces de machines, mais pas lorsque vous êtes plus intéressés par la création de films animés par ordinateur. OpenSCAD n'est pas un programme de modélisation interactif. Il est plus comme un compilateur 3D qui lit dans un fichier de script qui lui décrit l'objet et modélise le modèle 3D à partir de ce fichier de script (voir exemples ci-dessous). Cela permet de donner le contrôle total sur le processus de modélisation à l'utilisateur et vous permet de changer facilement toutes étapes du processus de modélisation ou de faire du design qui soit défini par des paramètres configurables."(http://openscad.org/, récupéré 22h58 17 Mars 2010 (UTC)
Voir aussi: l'usine Doblo (en), un ensemble de modules pour créer des structures, des briques et des mashups compatibles duplos, .
Création de notre premier modèle et l'interface
Premier modèle
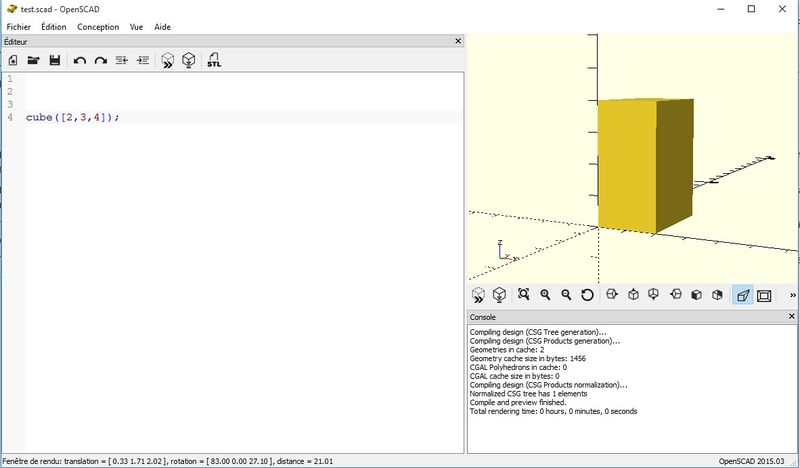
Pour notre premier modèle, nous créerons un simple parallélépipède de 2 x 3 x 4. Dans l'éditeur OpenScad, tapez la commande suivante sur une ligne :
cube([2,3,4]);
Ceci va définir un simple cube de taille x=2, y=3 et z=4.
Le parallélépipède peut maintenant être compilé et rendu comme nous allons le montrer ci-dessous
Le logiciel - Compiler le code Scad
L'interface ressemble à cela :
- A gauche, il y a une fenêtre d'édition. Bien sûr, vous pouvez aussi utiliser un éditeur externe.
- A droite, il y a la fenêtre de rendu
- Pour ouvrir un fichier .scad
- menu: Fichier->Ouvrir
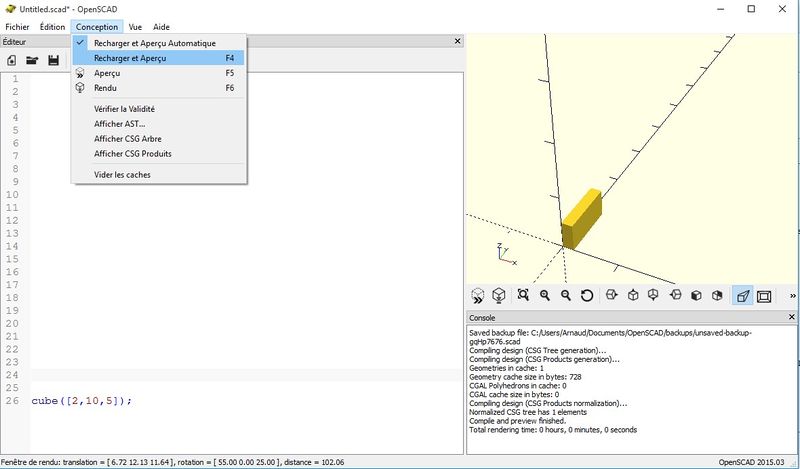
- Pour avoir un aperçu du résultat
- menu: Conception->Aperçu ou F5
- Utiliser menu: Conception->Recharger et aperçu ou F4. Si vous préférez utiliser un éditeur externe pour éditer du code .scad, le programme va détecter le changement de date du fichier et va automatiquement le recharger.
- Pour compiler et pour exporter
- menu: Conception -> Rendu (CGAL)ou F6 .... cela peut prendre plusieurs minutes. Cependant, les différentes parties sont mises en cache et le prochain rendu pourrait être beaucoup plus rapide.
- menu: Fichier -> Exporter --> Exporter comme un .STL
- Une fois que vous avez compilé et fait le rendu (CGAL)
- Vous pouvez consulter uniquement la grille CGAL (Menu: Vue->Wireframe ou F11)
- Le menu Vue
- Cochez "Afficher Axe"
- Vous pouvez basculer entre le mode "Open CSG"? et "Thrown together"? pour regarder le résultat
- Une fois qu'un objet est rendu (pas seulement compilé), vous pouvez explorer les autres options. Dans le même menu, vous trouverez différentes options à regarder comme compiler ou compiler modèles rendus. Explorez ceux-ci et rappelez-vous des raccourcis.
Des principes 3D
Il est bon de comprendre certaines terminologies du domaine de la 3D, afin d'être en mesure de suivre les instructions ou de comprendre pourquoi les choses peuvent mal se passer...
Modélisation polygonale : le modèle est assimilé à un ensemble de polygones : ce polyèdre est donc décrit par la liste des sommets et des arêtes. Si les polygones sont orientés, on pourra différencier l'extérieur et l'intérieur du modèle. Si l'on veut lever l'ambiguïté apportée par des polygones non plans, on utilisera uniquement des triangles : cette triangulation peut être forcée par le modeleur. Sans effet de lissage, l'objet apparaîtra anguleux si la définition en facettes est faible. En général, le lissage de Gouraud, réalisé par la carte graphique 3D, est suffisant pour donner un aspect plus lisse au modèle. La modélisation polygonale se sert d'outils de base identiques sur tous les logiciels 3D, ainsi que certains outils spécifiques aux logiciels génériques, aux logiciels spécialisés et aux plug-ins et scripts. Parmi ces outils, les plus répandus sont l'extrusion, la coupe (cut, split…), la soudure/rétractation (weld/collapse) et la révolution. L'extrusion consiste à surélever une ou plusieurs faces (adjacentes ou non) ou un profil 2D le long d'une trajectoire et de créer les faces venant combler le vide occasionné par le déplacement de l'élément de départ. Par exemple, extruder un cercle donne un cylindre ouvert ou un tuyau qui suit la trajectoire. La coupe consiste à créer des arêtes (edges) sur un maillage, ainsi que les points correspondants aux intersections des arêtes déjà existantes et celles nouvellement créées. On peut ainsi affiner un modèle, en ajoutant des détails sur certaines régions, notamment par l'ajout de boucles d'arêtes (edgeloops) extrêmement utilisées en modélisation organique. La soudure/rétractation consiste à souder les sommets (vertices) entre eux, pour simplifier un maillage, boucher des trous ou faire converger des arêtes. La révolution consiste à faire tourner un profil 2D autour d'un axe 3D : on obtient ainsi un volume de révolution. C'est la technique majoritairement utilisée dans le jeu vidéo, et le cinéma d'animation. La modélisation polygonale induit une marge d'erreur de proportions et de dimensions le plus souvent invisible à l'œil nu. Dans le cinéma d'animation, les modèles 3D organiques sont le plus souvent lissés. Le lissage consiste à subdiviser un maillage (une itération correspond à une subdivision de chaque arête, soit dans le cas de face à quatre côtés, une subdivision en quatre faces) et arrondir les faces obtenues selon différents algorithmes, afin de gommer l'effet anguleux des modèles obtenus par modélisation polygonale." (Modélisation polygonale, Wikipedia, récupéré le 28 Octobre 2015)
"En géométrie, un sommet est un type spécial de point qui décrit les coins ou les intersections de formes géométriques. Les sommets sont couramment utilisés en infographie pour définir les coins de surfaces (triangles généralement) dans des modèles 3D, où chaque point est donné comme un vecteur. Un sommet d'un polygone est le point d'intersection entre deux bords, un sommet d'un polyèdre est le point d'intersection de trois ou plusieurs bords ou faces." (Vertex geometry, Wikipedia, récupéré à 17h25, le 23 Mars 2010 (UTC))
Les faces ou facettes définissent la surface d'un objet en 3 dimensions, à savoir ce qui est entre "l'extérieur" et "l'intérieur".
"De nombreux programmes de modélisation ne respectent pas strictement la théorie géométrique; par exemple, il est possible pour deux sommets d'avoir deux bords distincts qui les relie, occupant la même position spatiale. Il est également possible pour deux sommets d'exister dans les mêmes coordonnées spatiales, ou à deux faces d'exister au même endroit. De telles situations ne sont généralement pas souhaités et de nombreux logiciels 3D possèdent une fonction d'auto-nettoyage. Si l'auto-nettoyage est pas présent, ils doivent être supprimés manuellement." (Vertex geometry, Wikipedia, récupéré à 17h25, le 23 Mars 2010 (UTC))
"Un groupe de polygones qui sont reliés entre eux par des sommets partagés sont désignés par une maille. Pour avoir un bon maillage lors du rendu, il est souhaitable que ce soit une non auto-intersection, ce qui signifie qu'aucun bord passe par un polygone. Une autre façon de voir les choses est que le maillage ne peut pas se percer. Il est également souhaitable que le treillis ne contienne pas d'erreurs tel que des sommets, des arêtes ou des faces doublés. Pour certaines applications, il est important que le maillage soit un "manifold" c'est à dire qu'il ne contient pas de trous ou de singularités (endroits où deux sections distinctes de la maille sont reliés par un seul sommet)" (Vertex geometry, Wikipedia, récupéré à 17h25, le 23 Mars 2010 (UTC))
"Dans de nombreux formats, par exemple STL et OpenSCAD, le principe est le suivant: "(i) La normale et chaque sommet de chaque facette sont spécifiées par trois coordonnées chacun, donc il y a un total de 12 numéros mémorisés pour chaque facette. (ii) Chaque facette fait partie de la frontière entre l'intérieur et l'extérieur de l'objet. L'orientation des facettes (où est le `` sortir et où est le `` dedans) est spécifié redondante de deux manières qui doivent être conformes. En premier lieu, la direction de la normale est vers l'extérieur. Deuxièmement, les sommets sont répertoriés dans l'ordre dans le sens antihoraire quand on regarde l'objet de l'extérieur (règle de la main droite). (iii) Chaque triangle doit partager avec deux sommets de chacun de ses triangles adjacents. Ceci est connu comme règle sommet à sommet. (iv) L'objet représenté doit être situé dans l'octant tout-positive (toutes les coordonnées des sommets doivent être positifs)." (Daniel Rypl, Zdenek Bittnar 2004, récupéré Avril de 2010.
"La normale ou la surface normale est un vecteur qui est perpendiculaire à une face." Surface normale, Wikipedia, récupéré 15h07, le 20 Novembre 2011 (UTC)
Exemples de code
Utilisant des modèles existants
Il est préférable d'apprendre d'abord comment utiliser les modules OpenSCAD "ready-made". Télécharger à partir d'un endroit comme thingverse.
La plupart de ces fichiers définissent modules (fonctions aka) que vous ne pouvez exécuter avec ou sans paramètres afin de faire un rendu d'un modèle.
Modules sans paramètres:
Les exemples "bloqueurs de porte" de Thingiverse que vous pouvez télécharger ici chose 2,154 sont définis comme deux modules en un seul fichier * .scad, porte-bouchon-2.scad. Télécharger ou copier / coller le code à partir d'ici. Bien sûr, ces modules d'arrêt de porte peuvent être paramétrées, mais cela peut être fait avec des variables comme vous pouvez le voir.
Modules avec paramètres:
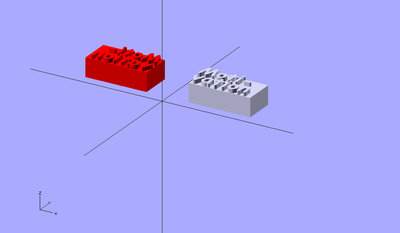
Le bloc paramétrique Lego / Duplo d'autre part (chose 2014) peut inclure des paramètres, par exemple, vous pourriez l'appeler comme cela pour une petite brique de 2x2x3 avec des "nibbles".
Duplo (1,1,3, true);
ou comme cela pour une plus grande brique sans "nibbles".
Duplo (2,2,4, false);
Juste essayer: compiler et modifier les paramètres si ils ne vous conviennent pas. Nous avons également créé une usine de Doblo plus sophistiquée qui peut aussi être étudiée.
Modules avec des paramètres nommés:
Vous pouvez également utiliser des noms de paramètres plutôt que de simplement utiliser des positions. L'exemple suivant peut être fait avec l'usine de Doblo.
doblo (col=0,
row=4,
up=0,
width=4,
length=2,
height=FULL,
nibbles_on_off=true,
diamonds_on_off=false,
scale=LUGO);
Si les paramètres par défaut sont définis, vous pouvez tapez simplement
doblo ();
afin d'obtenir une hauteur typique des brique Lego compatible 4x2.
Si vous préférez apprendre plus sur OpenSCAD avant d'essayer, ignorez ces exemples et revenez y plus tard.
Un simple bloqueur de porte
Le code suivant va créer un butoir de porte. Au lieu d'essayer de comprendre cet exemple, vous pouvez aussi le sauter et lire le reste de cet article en premier.
Pour utiliser ce module, vous devrez ajouter la ligne suivante dans le code. C'est à dire que cela va appeler le module "door_stopper_simple":
door_stopper_simple ();
</ source>
<source lang="javascript">
// To use it, uncomment
// door_stopper_simple ();
module door_stopper_simple ()
{
height = 20 ;
length = 125 ;
width= 40 ;
half_width = width / 2;
borders = 10; // 1 cm on each side
top_cube_length = length - 4 * borders;
top_cube_width = width - 2 * borders;
top_cube_height = height ; // make it big enough
top_z = height/2 + 4 ; // adjust manually ;)
tip_cut_pos = length/2 - 0.5;
difference() {
translate ([-length/2.0, 0, 0]) {
polyhedron (
points = [[0, -half_width, height], [0, half_width, height], [0, half_width, 0], [0, -half_width, 0], [length, -half_width, 0], [length, half_width, 0]],
triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5], [5,2,4], [4,2,3], ]);
}
// top inset
translate ([-1 * borders, 0, top_z]) {
# cube ([top_cube_length,
top_cube_width,
top_cube_height],
center=true) ;
}
// cut of the tip a bit
translate ([tip_cut_pos, 0, 0]) {
# cube ([20,
width + 1,
height],
center=true) ;
}
}
}
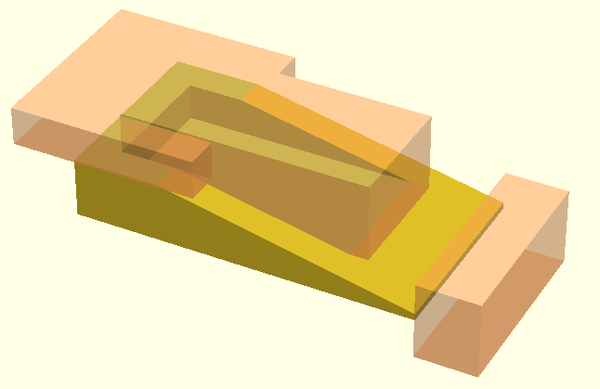
Bloqueur de porte
Le modèle suivant est un peu plus sophistiqué.
Pour l'utiliser: door_stopper ();
// To use it, uncomment
// door_stopper ();
module door_stopper ()
{
height = 25 ;
length = 120 ;
width= 60 ;
half_width = width / 2;
borders = 10; // 1 cm on each side
// params for bottom inset
bottom_cube_length = length - 4 * borders;
bottom_cube_width = width - 2 * borders;
bottom_cube_height = 6.0 ; // 3mm in / 3mm outsite
bottom_z = 0;
// params for top inset
top_cube_length = length - 4 * borders;
top_cube_width = width - 2 * borders;
top_cube_height = height ; // make it big enough // 25
top_z = height/2 + 7.5 ; // 12.5 + 7.5 = 10 ; 10 - 2.5 = 7.5
// param for tip
tip_cut_pos = length/2 - 0.5;
// param for top tip
top_tip_pos = height + 0.5;
difference() {
translate ([-length/2.0, 0, 0]) {
polyhedron (
points = [[0, -half_width, height], [0, half_width, height], [0, half_width, 0], [0, -half_width, 0], [length, -half_width, 0], [length, half_width, 0]],
triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5], [5,2,4], [4,2,3], ]);
}
// bottom inset
translate ([-1 * borders, 0, bottom_z]) {
# cube ([bottom_cube_length,
bottom_cube_width,
bottom_cube_height],
center=true) ;
}
// top inset
translate ([-1 * borders, 0, top_z]) {
# cube ([top_cube_length,
top_cube_width,
top_cube_height],
center=true) ;
}
// cut of the top tip a bit
translate ([- length/2 + 10, 0, top_tip_pos]) {
# cube ([length / 2,
width+2,
height / 2],
center=true) ;
}
// cut of the front tip a bit
translate ([tip_cut_pos, 0, 0]) {
# cube ([20,
width + 1,
height],
center=true) ;
}
}
}
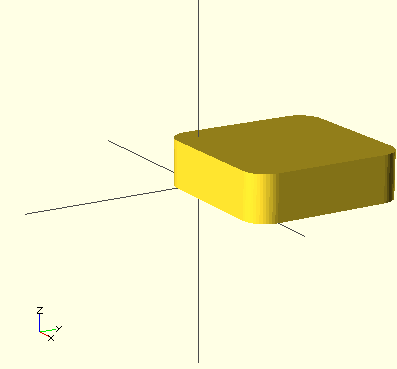
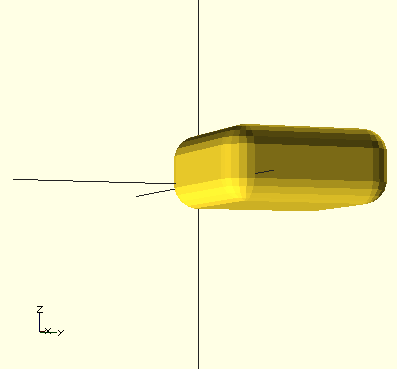
Vous pourriez alors aussi ajouter un texte comme celui-ci. Je l'ai fait en utilisant Netfabb Pro. Il permet de créer du texte en 3D et à assembler les différentes parties en un seul .STL.
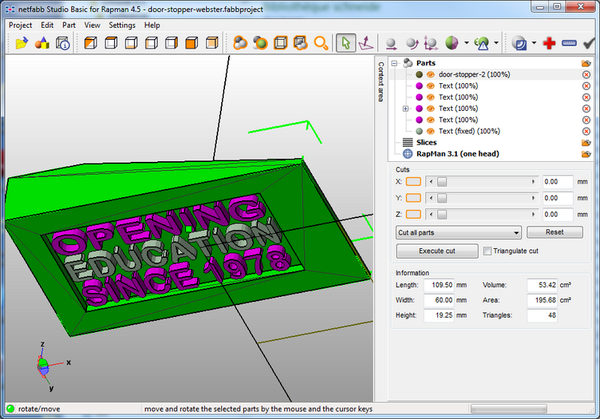
Le résultat une fois imprimé :

Le bloc parametrique Lego Duplo
Ce code est un dérivé du bloc Lego Duplo paramétrique . C'est le code OpenSCAD le plus compliqué avec lequel nous ayons joué jusqu'ici. Domonoky. Nous l'avons également uploadé sur Thingyverse. Les personnes ayant une bonne formation en mathématiques peuvent obtenir beaucoup plus hors du logiciel OpenSCAD ....
//the duplo itself
// parameters are:
// width: 1 =standard 4x4 duplo with.
// length: 1= standard 4x4 duplo length
// height: 1= minimal duplo height
// nibbles: true or false
duplo(1,1,3,true);
module duplo(width,length,height,nibbles)
{
//size definitions
ns = 8.4; //nibble start offset
no = 6.53; //nibbleoffset
nbo = 16; // nibble bottom offset
duplowidth = 31.66;
duplolength=31.66;
duploheight=9.6;
duplowall = 1.55;
//the cube
difference() {
cube([width*duplowidth,length*duplolength,height*duploheight],true);
translate([0,0,-duplowall])
cube([width*duplowidth - 2*duplowall,length*duplolength-2*duplowall,height*duploheight],true);
}
//nibbles on top
if (nibbles)
{
for(j=[1:length])
{
for (i = [1:width])
{
translate([i*ns+(i-1)*no,j*ns+(j-1)*no,6.9+(height-1)*duploheight/2]) duplonibble();
translate([i*-ns+(i-1)*-no,j*ns+(j-1)*no,6.9+(height-1)*duploheight/2]) duplonibble();
translate([i*ns+(i-1)*no,j*-ns+(j-1)*-no,6.9+(height-1)*duploheight/2]) duplonibble();
translate([i*-ns+(i-1)*-no,j*-ns+(j-1)*-no,6.9+(height-1)*duploheight/2]) duplonibble();
}
}
}
//nibble bottom
for(j=[1:length])
{
for (i = [1:width])
{
translate([(i-1)*nbo,(j-1)*nbo,0]) duplobottomnibble(height*duploheight);
translate([(i-1)*-nbo,(j-1)*-nbo,0]) duplobottomnibble(height*duploheight);
translate([(i-1)*-nbo,(j-1)*nbo,0]) duplobottomnibble(height*duploheight);
translate([(i-1)*nbo,(j-1)*-nbo,0]) duplobottomnibble(height*duploheight);
}
}
//little walls inside[http://www.thingiverse.com/Domonoky Domonoky]
difference()
{
union()
{
for(j=[1:length])
{
for (i = [1:width])
{
translate([0,j*ns+(j-1)*no,0 ]) cube([width*duplowidth,1.35,height*duploheight],true);
translate([0,j*-ns+(j-1)*-no,0 ]) cube([width*duplowidth,1.35,height*duploheight],true);
translate([i*ns+(i-1)*no,0,0 ]) cube([1.35,length*duplolength,,height*duploheight],true);
translate([i*-ns+(i-1)*-no,0,0 ]) cube([1.35,length*duplolength,height*duploheight],true);
}
}
}
cube([width*duplowidth - 4*duplowall,length*duplolength-4*duplowall,height*duploheight+2],true);
}
}
module duplonibble()
{
difference() {
cylinder(r=4.7,h=4.5,center=true,$fs = 0.01);
cylinder(r=3.4,h=5.5,center=true,$fs = 0.01);
}
}
module duplobottomnibble(height)[http://www.thingiverse.com/Domonoky Domonoky]
{
difference() {
cylinder(r=6.6,h=height,center=true,$fs = 0.01);
cylinder(r=5.3,h=height+1,center=true,$fs = 0.01);
}
}
Le langage OpenScad
Modules
Les modules peuvent être grossièrement comparées aux fonctions, macros ou à des sous programmes dans un langage de programmation. Avec ces modules vous pouvez définir du code réutilisable.
Exemple:
- Le module appelé "thing" est appelé par le module appelé "demo_proj".
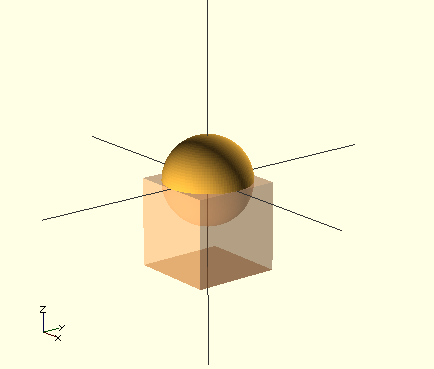
Source: Example021.scad livré avec la distribution du logiciel
module thing()
{
$fa = 30;
difference() {
sphere(r = 25);
cylinder(h = 62.5, r1 = 12.5, r2 = 6.25, center = true);
rotate(90, [ 1, 0, 0 ]) cylinder(h = 62.5,
r1 = 12.5, r2 = 6.25, center = true);
rotate(90, [ 0, 1, 0 ]) cylinder(h = 62.5,
r1 = 12.5, r2 = 6.25, center = true);
}
}
module demo_proj()
{
linear_extrude(center = true, height = 0.5) projection(cut = false) thing();
thing();
}
demo_proj();
- Les modules peuvent être embarqués à l'intérieur d'autres modules et peuvent bien évidemment avoir des paramètres.
Contrôle du flux
Boucle For
Une boucle for itère sur les valeurs d'un vecteur ou sur une intervalle.
Syntaxe:
for (loop_variable_name = range or vector) {
.....
}
- Paramètres
- loop_variable_name = Nom de la variable à utiliser dans la boucle For.
- range: [low : high]. Low et high peuvent être tout aussi bien des nombre ou des variables.
- vector: Un vecteur comme [1,2,10,40.5]
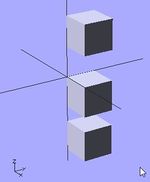
Exemples d'utilisation: Une boucle For utilisant un vecteur.
for ( z = [-1, 1, -2.5]) {
translate( [0, 0, z] )
cube(size = 1, center = false);
}
Une boucle For utilisant une intervalle
for ( i = [0:5] ) {
rotate( i*360/6, [1, 0, 0])
translate( [0, 10, 0] ) sphere(r = 1);
}
Intersection boucle For
Une intersection boucle for itère sur un vecteur de vecteurs, entraînant une intersection/chevauchement de tous les objets générés.
Syntaxe:
intersection_for (loop_variable_name = vector_of_vectors) {
.....
}
- Paramètres
- loop_variable_name = Nom de la variable à utiliser dans la boucle For.
- vector_of_vectors: Un vecteur comme [ [1,2,10],[14,-20.3,40.5] ]
Exemple d'utilisation 1 - rotation :
intersection_for(i = [
[0, 0, 0],
[10, 20, 300],
[200, 40, 57],
[20, 88, 57]
])
rotate(i) cube([100, 20, 20], center = true);
Exemple d'utilisation 2 - translation
intersection_for(i = [
[0, 0, 0],
[2, 1, 1],
[-2, 1, 0]
])
translate (i) cylinder(r=5, h=10, center = true);
La condition If
La condition if permet d'évaluer conditionnellement une sous-arborescence.
Syntaxe
if (boolean_expression) { .... }
if (boolean_expression) { .... } else {.... }
if (boolean_expression) { .... } else if (boolean_expression) {.... }
if (boolean_expression) { .... } else if (boolean_expression) {.... } else {....}
Paramètres
- L'expression booléenne qui devrait être utilisée en tant que condition.
Exemple d'utilisation 1:
if (x > y) {
cube(size = 1, center = false);
}
Exemple d'utilisation 2:
SCALE = 0.5 ;
... autres variables .....
module doblonibble() {
// Les Lego redimensionnés n'ont pas de trous dans les tétines
if (SCALE < 0.6) {
cylinder(r=NB_RADIUS, h=NH, center=true, $fs = 0.05);
} else {
difference() {
cylinder(r=NB_RADIUS,h=NH, center=true, $fs = 0.05);
cylinder(r=NB_RADIUS_INSIDE,h=NH+1,center=true, $fs = 0.05);
}
}
}
Variables et instructions d'affectation
Variables
L'affectation des variables prend la même syntaxe qu'en C. Exemple:
SCALE = 1;
ou
PART_HEIGHT = ((SCALE < 0.6) && LEGO_DIV) ? 3.2 * LEGO_SCALE : 4.8 * SCALE ;
Cependant et n'oubliez pas ça:
- OpenScad calcule ses variables au moment de la compilation, et pas au moment de l'exécution du code, ce qui veut dire que la dernière affectation de la variable sera appliquée partout où la variable est utilisée..
- Cela devrait aider si on les considère plutôt comme des constantes dont la valeur est modifiable que des variables. Ceci veut dire que vous pouvez fixer des variables dans une librairie et ensuite les modifier dans le fichier qui chargera la librairie. Vous ne pouvez pas affecter deux valeurs différentes à la même variable quand vous calculez un model!
Assign
Fixe une nouvelle valeur à une variable dans une sous-arborescence. Cela peut être utilisé dans un module pour stocker des valeurs intermédiaires. Dans l'exemple
Syntaxe:
assign (var1= expr1, var2= expr2, ....)
Exemple démontrant que les variables sont (re)affectables:
for (i = [10:50])
assign (angle = i*360/20, distance = i*10, r = i*2) {
rotate(angle, [1, 0, 0])
translate( [0, distance, 0] ) sphere(r = r);
}
La variable "angle" local, "distance" and "r" sont modifiées à chaque cycle de la boucle.
Remarque: La fonction assign sera supprimés dans les prochaines version d'OpenScad. Il est donc conseillé de faire une affectation classique: var1= expr1; var2= expr2; ...
et for (i = [10:50], angle = i*360/20, distance = i*10, r = i*2)
{
rotate(angle, [1, 0, 0])
translate( [0, distance, 0] ) sphere(r = r);
}
Opérateurs mathématiques et fonctions
Les opérateurs OpenScad semble fonctionner comme dans les autres langages se basant sur C. Regardez les détails dans la manuel officiel:
Les conditions sont aussi implémentées. Exemple: condition ? if_true_expression : if_false_expression
Exemple:
HEIGHT = (SCALE < 0.5) ? 3 : 6*1/1 ;
- If Ceci veut dire que si SCALE==0.6, alors HEIGHT vaudra 6. Si SCALE est plus petite que 0.5 alors HEIGHT==3.
Fonctions
Les fonctions peuvent être utilisées pour définir des modules utilitaires simples. À ne pas confondre avec les "modules".
Variables spéciales
Comme expliqué dans le wiki d' OpenScad , les variables commençant par un '$' sont des variables spéciales.
Avis pour les programmeurs: La sémantique des variables spéciales est similaire à celle des variables spéciales en lisp: Elles ont une portée dynamique plutôt qu'une portée lexicale. Ce qui veut dire que leur valeur est définie au moment de l'exécution du code. Par exemple, imaginons que vous commencez un code avec $fa = 5, puis vous appelez un module A dans lequel vous définissez $a = 7. Alors quand le module A appelle encore un autre module B, la seconde affectation ($a==7) sera utilisée.
Les variables spéciales $fa, $fs et $fn contrôlent le nombre de facettes utilisées pour générer un arc. Comme expliqué au-dessus, vous pouvez les modifier dans chaque module.
- $fa
- $fa est l'angle du fragment. Cela fixe l'angle minimum pour un fragment. Même un grand cercle n'a pas plus de fragments que 360 divisé par ce nombre. La valeur par défaut est de 12 (ce qui donne 30 fragments pour un cercle entier).
- $fs
- $fs est la taille du fragment and définit la taille minimum pour un fragment. À cause de cette variable, de très petits cercles ont un plus petit nombre de fragments que ceux qui sont spécifiés en utilisant $fa. Les valeur par défaut est 1.
- $fn
- $fn est le nombre de fragments. C'est souvent 0. Quand cette variable a une valeur plus grande que 0, les deux autres variables sont ignorées et un cercle entier est construit en utilisant ce nombre de fragments. La valeur par défaut est 0.
La forme d'un cercle peut être améliorée en fixant une des variables spéciales $fn, $fs et $fa. Lorsque $fa et $fs sont utilisées pour déterminer le nombre de fragments pour un cercle alors OpenScad n'utilisera jamais moins de 5 fragments.
Si vous voulez accélerer la construction pour un test, une bonne astuce est de fixer un nombre de facettes très bas au début du script. Tant que $fn est une variable spéciale, alors cela affectera tous les objets sauf si elle est remodifiée par la suite.
Exemple avec une résolution basse $fn=10; Exemple avec une haute résolution
$fn=100;
Haute résolution veut dire plus de triangles et plus d'attente :) Dans la plus part des cas, 20-50 devrait être suffisant pour une impression 3D.
Solides primitifs
OpenScad a les primitives "habituelles", comme par exemple les cubes, les cylindres et les sphères.
Les coordonnées sont définies sous forme de tableaux. Par exemple [2,3,4] veut dire x = 2, y = 3 et z = 4.
Cube
La primitive cube permet de créer un cube à l'origine du système de coordonnées. Quand le paramètre "center" vaut true alors le cube sera centré à l'origine, autrement il est créé dans le premier octant. Les noms des paramètres sont facultatifs si les paramètres sont donnés dans le même ordre qu'il est spécifié sous "paramètres".
Paramètres:
- size
- Décimale ou 3 valeurs sous forme de tableau. Si un seul nombre est donné, alors le résultat sera un cube avec tous les côtés ayant cette longueur. Si 3 valeurs sous forme de tableau sont données, alors les valeurs correspondront aux longueurs des côtés X, Y et Z. La valeur par défaut est 1.
- center
- Booléen. Cela détermine le positionnement de l'objet. Si ce paramètre prend la valeur true, l'objet sera alors centré à (0, 0, 0). Autrement, le cube est placé dans le quadrant positif avec un coin sur (0, 0, 0). La valeur par défaut est false.
Exemple 1:
cube ([2,3,4])
Exemple 2:
bottom_cube_length = 2; bottom_cube_width = 3; bottom_cube_height = 2; cube ([bottom_cube_length, bottom_cube_width, bottom_cube_height], center=true) ;
Exemple 3:
cube(size = 1, center = false); cube(size = [1,2,3], center = true);
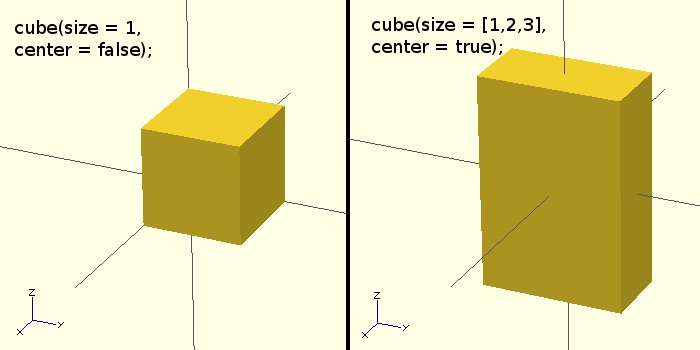
Sphere
La primitive sphere créé une sphère à l'origine du système de coordonnées. Les noms des paramètres sont optionnels.
- Paramètres
- r
- Décimal. C'est le rayon de la sphère. La résolution de la sphère sera basée sur la taille de la sphère et sur les variables spéciales $fa, $fs et $fn.
Exemple d'utilisation
sphere(r = 1); sphere(r = 5); sphere(r = 10); sphere(2, $fn=100); // Sphère avec 2mm de rayon en haute résolution sphere(2, $fa=5, $fs=0.1); // Sphère avec 2mm de rayon en (moins) haute résolution
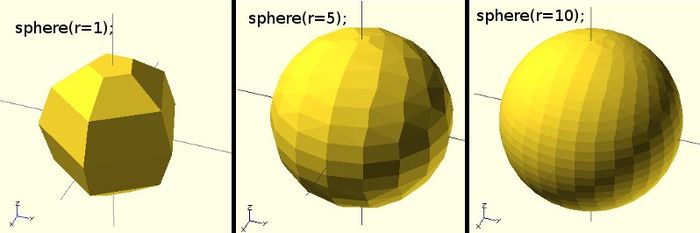
Cylinder
La primitive cylinder créé un cylindre à l'origine du système de coordonnées. Quand les deux rayons du cylindre sont égaux il est aussi possible de spécifier un seul rayon en spécifiant "r" comme nom de paramètre. Les noms des paramètres sont facultatifs si les valeurs sont données dans le même ordre qu'il est spécifié ci-dessous.
Paramètres
- h
- Décimal. C'est la hauteur du cylindre. La valeur par défaut est 1.
- r1
- Décimal. C'est le rayon de la partie haute du cylindre/cône. La valeur par défaut est 1.
- r2
- Décimal. C'est le rayon de la partie basse du cylindre/cône. La valeur par défaut est 1.
- r
- Décimal. C'est le rayon de la partie haute et la partie basse du cylindre. Utilisez ce paramètre si vous voulez un cylindre qui ressemble à un pilier et non pas à un cône. La valeur par défaut est 1.
Exemples d'utilisation
cylinder(h = 10, r1 = 10, r2 = 20, center = false); cylinder(h = 10, r1 = 20, r2 = 10, center = true); cylinder(h = 10, r=20);
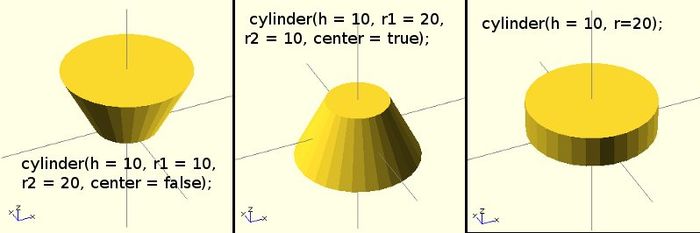
Polyhedrons
Les polyèdre sont les formes les plus difficiles à traiter. A la place d'utiliser cette fonction, vous devriez (a) penser à comment vous pourriez combiner des formes simples pour arriver au même résultat ou (b) regarder sous l'extrusion 2D.
- Un polyèdre est souvent définit comment étant un solide géométrique avec des faces plates et des côtés droits.(Wikipedia, 17:25, 23 mars 2010 (UTC)).
Tout polyèdre peut être construit à partir de différentes sortes d'éléments ou entités, chacune associées avec différents nombres de dimensions.
- 3 dimensions: Le corps est limité par les faces, et est a normalement le volume enfermé dans ces surfaces.
- 2 dimensions: Une face est un polyèdre délimité par le contour des bords, et normalement inclut les régions plates (plan) dans la limite. Ces faces polygonales, ensembles font la surface du polyèdre.
- 1 dimension: Un bord rejoint un sommet à un autre et une face à une autre. Il s'agit normalement d'un segment. Les bords ensemble font le squelette du polyèdre.
- 0 dimensions: Un sommet (plural vertices) est un point.
(Wikipedia, 17:25, 23 mars 2010 (UTC)).
Syntaxe:
polyhedron(points = [ [x, y, z], ... ], triangles = [ [p1, p2, p3..], ... ], convexity = N);
La primitive polyhedron créé un polyèdre avec des points et triangles spécifiques. (Les composant des vecteurs des triangles 'pN' sont 0-indexés faisant référence aux éléments des points du vecteur.)
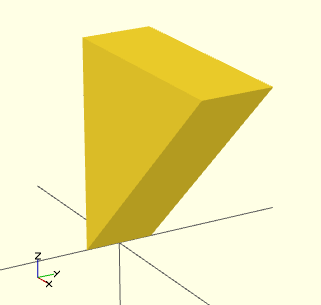
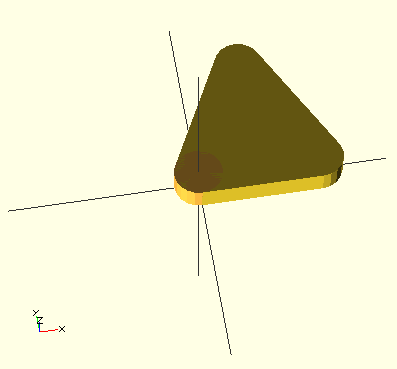
Exemple (voir l'image en dessous)
polyhedron ( points = [[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60]], triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5], [5,2,4], [4,2,3], ]);
Remarquez qu'OpenSCAD crash si vos polygones ne sont pas orientés de la même façon. Faites attention à l'ordre des sommets (Ne comprenez pas ça!) Exemple:
polyhedron(points=[[0,0,0],[100,0,0],[0,100,0],[0,100,100]], triangles=[[0,1,2],[0,1,3],[0,2,3],[1,2,3]]); //Crash polyhedron(points=[[0,0,0],[100,0,0],[0,100,0],[0,100,100]], triangles=[[0,1,2],[1,0,3],[0,2,3],[2,1,3]]); //Fonctionne
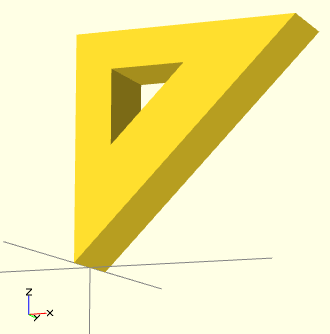
Un autre exemple:
Voyons maintenant comment réparer des polyèdres avec des polygones mal orientés. Quand vous sélectionnez 'Jeté ensemble' dans le menu Vue et que vous compilez le design (pas le compilé et rendu!) vous allez voir un aperçu avec les polygones mal orientés mis en évidence. Malheureusement cette mise en évidence n'est pas possible avec l'aperçu du mode OpenCSG parce que cela ferait une interférence avec la façon dont l'aperçu dans le mode OpenCSG est implémenté.
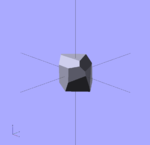
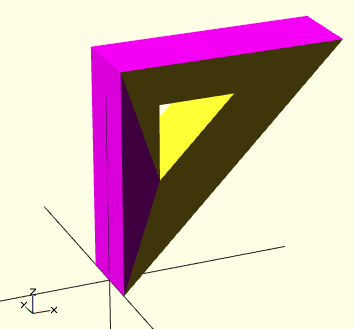
Ci-dessous vous pouvez voir un polyèdre problématique. Les mauvais triangles sont en violet.
// Mauvais polyèdre
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
triangles = [
[0,2,3], [0,1,2], [0,4,5], [0,5,1], [5,4,2], [2,4,3],
[6,8,9], [6,7,8], [6,10,11], [6,11,7], [10,8,11],
[10,9,8], [0,3,9], [9,0,6], [10,6, 0], [0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,7,8],
[1,8,2], [2,8,11], [2,11,5]
]
);
Un polyèdre correcte serait le suivant:
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
triangles = [
[0,3,2], [0,2,1], [4,0,5], [5,0,1], [5,2,4], [4,2,3],
[6,8,9], [6,7,8], [6,10,11],[6,11,7], [10,8,11],
[10,9,8], [3,0,9], [9,0,6], [10,6, 0],[0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],
[2,8,1], [8,2,11], [5,11,2]
]
);
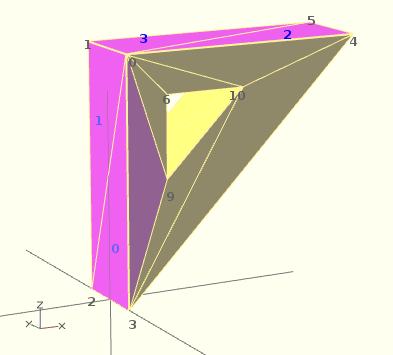
Astuces pour les débutants: Si vous ne comprenez pas vraiment l'"orientation", alors identifiez simplement les triangles mal orientés puis permutez l'ordre correspondant des triangles et les sommets jusqu'à ce que vous arriviez au résultat correcte. Par exemple dans l'exemple en dessus, le troisième vecteur de triangle ([0, 4, 5]) était mauvais et nous l'avons réparé en mettant [4, 0, 5]. De plus vous devriez sélectionner "Afficher les arrêtes" dans le menu "Vue", faire une capture d'écran, l'imprimer et numéroter les sommets (points) et les triangles. Dans notre exemple, les points sont en noir et les triangles sont en bleu. Ensuite, tournez autour de l'image sur OpenScad et faites une seconde copie du dos si besoin.
Remarque: Le paramètre triangle sera supprimés dans les prochaines version d'OpenScad. Il est donc conseillé de mettre "faces" à la place. Exemple:
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
faces = [
[0,3,2], [0,2,1], [4,0,5], [5,0,1], [5,2,4], [4,2,3],
[6,8,9], [6,7,8], [6,10,11],[6,11,7], [10,8,11],
[10,9,8], [3,0,9], [9,0,6], [10,6, 0],[0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],
[2,8,1], [8,2,11], [5,11,2]
]
);
Transformations
scale
La commande scale redimensionne sont élément enfant en utilisant le vecteur spécifié. Le nom du paramètre v est facultatif.
- Syntaxe
- scale(v = [x, y, z]) { ... }
- Exemple
- Créé un ovale de longueur = 40 dans la direction de x; y et z restent pareils.
scale (v=[2,1,1]) cylinder(h = 10, r=20);
rotate
La commande rotate accepte plusieurs versions de paramètres.
- Syntaxe pour une rotation 2D autour de l'axe Z
rotate (deg)
Exemple:
- rotate(45) square(10);
- Syntaxe pour des rotations sur plus d'un axe
- rotate(a = deg, v = [x, y, z]) { ... }
Effectue une rotation à son élément enfant de a degrés autour du vecteur v spécifié enraciné sur l'origine du système des coordonnées.
Paramètres:
- a
- Degrés
- v
- Un tableau de [x,y,z]
Exemple: Effectue une rotation sur l'objet produit par le module 8bit_char de 270 degrés autour de l'axe z.
rotate (a=270, v=[0,0,1]) {
8bit_char(char, size_mm, height);
}
- Syntaxe alternative
- rotate(a = [deg_x,deg_y,deg_z] { ... }
Paramètres:
- a
- Vecteur de trois degrés. Dans ce cas les nœuds enfants effectuent une rotation autour de l'axe positif x, y et z (dans cet ordre) par les nombres spécifiés en degrés.
Par exemple, pour basculer un objet d'en haut à en bas, vous devriez faire ça:
rotate(a=[0,180,0]) { ... }
Astuce: Le nom des paramètres sont facultatifs s'ils sont donnés dans le même ordre qu'il est spécifié en dessus.
translate
- Syntaxe
- translate(v = [x, y, z]) { ... }
La commande translate applique une translation (bouge) à son élément enfant le long du vecteur spécifié. Le nom du paramètre est facultatif.
mirror
- Syntaxe
- mirror([ 1, 0, 0 ]) { ... }
La commande mirror effectue un miroir sur son élément enfant au travers l'origine. Le paramètre pour effectuer la commande mirror() est le vecteur normal sur ce plan.
translate ([-100,0,0]) import("motivation.stl");
color ("red") {
mirror ([1,0,0]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
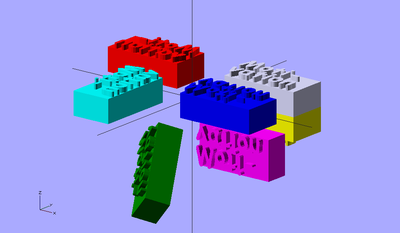
Imaginez un plan orthogonal à l'axe X qui passe au travers de l'origine. Ce sera le miroir.
translate ([-100,0,0]) import("motivation.stl");
color ("red") {
mirror ([1,0,0]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
color ("blue") {
mirror ([0,1,0]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
color ("cyan") {
mirror ([1,1,0]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
color ("yellow") {
mirror ([0,0,1]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
color ("magenta") {
mirror ([0,1,1]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
color ("green") {
mirror ([1,1,1]) {
translate ([-100,0,0]) import("motivation.stl");
}
};
multmatrix
- Syntaxe
- multmatrix(m = [...]) { ... }
Exemple (translate par [10, 20, 30]):
multmatrix(m = [ [1, 0, 0, 10],
[0, 1, 0, 20],
[0, 0, 1, 30],
[0, 0, 0, 1]
]) cylinder();
Multiplie la géométrie de tous les éléments enfant avec la matrice de transformation donnée 4x4.
color
Exemple d'utilisation:
color([r, g, b, a]) { ... }
La commande color affiche les éléments enfant en couleur en utilisant la couleur RGB spécifiée + la valeur alpha. C'est simplement utilisé pour le OpenCSG et le mode d'affichage jeté ensemble. La valeur d'alpha sera par défaut à 1.0 (opaque) si elle n'est pas spécifiée.
Notez bien que les valeurs r, g, b et a sont limitées à des valeurs décimales dans l'intervalle { 0.0 ... 1.0 } plutôt qu'aux entier traditionnels { 0 ... 255 }. Cependant si vous voulez mettre les entiers traditionnels vous pouvez contourner cette contrainte en spécifiant vos valeurs dans des fractions. Par exemple pour les entier R, G, B compris dans { 0 ... 255 } vous pouvez utiliser:
color([ R/255, G/255, B/255 ]) { ... }
Si vous avez juste besoin de couleurs simples, utilisez quelque chose comme (Toutes les CSS2/X11 devraient faire):
color("red") cube () ;
Regardez la table CSS3 des noms de couleur
minkowski
sommes Minkowski permet d'ajouter chaque élément de A à chaque élément de B. Ce n'est pas facile à comprendre. Vous devriez aussi lire
allow to add every element of A to every element of B. Not easy to understand and you also may read somme minkowski sur cgal.org.
Provenant du Manuel OpenScad:
$fn=50;
minkowski() {
cube([10,10,2]);
// coins arrondis
cylinder(r=2,h=2);
}
Pour avoir des coins arrondis de partout, on pourrait utiliser une sphère.
Si vous fixez $fn=50, cela prendra du temps à calculer.
$fn=20;
minkowski() {
cube([10,10,2]);
// coins arrondis
sphere(2);
}
hull
La commande hull va créer une coque à partir des objets qui se trouvent à l'intérieur. Lisez convex hull sur cgal.org si vous voulez comprendre le principe.
$fn = 20;
hull () {
# translate([0,0,0]) cylinder(r=2,h=2);
translate([10,0,0]) cylinder(r=2,h=2);
translate([5,10,0]) cylinder(r=2,h=2);
}
Modélisation CSG
Principe
CSG veut dire Constructive solid geometry.
Il est possible de créer un modèle 3D complexe en combinant de simples objets 3D primitifs, comme des cubes, des cylindres ou des sphères.
Fusion d'objets
Le résultat de l'union donnera une seule forme. Par exemple si vous entassés des cubes alignés les uns contre les autres, le résultat sera une forme (sans murs internes). C'est le comportement idéal pour une imprimante rapman. Notez cependant, que la juxtaposition d'objets car peut se passer mal. Par exemple deux cubes ne peuvent pas partager un seul même coin comme expliqué plus tard.
Exemple 1:
union() {
translate(0,0,x) import_stl("duck.stl");
duplo(2,2,1.5,false);
}
Exemple 2 (voir l'image ci-dessous)
union() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
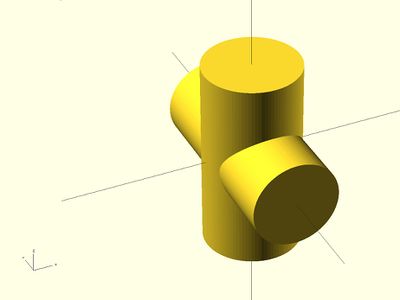
Difference
La commande difference soustrait le deuxième ( et les suivants) nœuds enfant à partir du premier
Exemple 1:
difference() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}

Exemple 2:
difference() {
// start objects
cylinder (h = 4, r=1, center = true, $fn=100);
// first object that will substracted
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
// second object that will be substracted
rotate ([90,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Vous devriez toujours vous assurer que l'objet qui extrait est plus long ou plus court que l'objet qui subira les extractions. Sinon vous pouvez aller sous "problèmes d'objets non 2-manifold" décrits sous la section de dépannage.
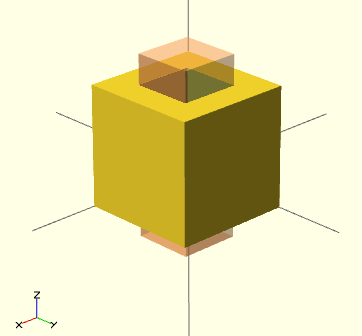
Manifold veut dire que c'est "étanche à l'eau et qu'il n'y a pas de trous dans la géométrie. Dans un valide 2-manifold chaque coin doit connecter exactement deux facettes. Cela veut dire que le programme doit être capable de connecter une face avec un objet. Par exemple si vous utilisez un cube avec une hauteur de 10 pour extraire quelque chose d'un cube plus large que celui qui a 10 de hauteur, ce n'est pas évident de savoir à qui des deux cubes le sommet ou le bas appartient. Alors faites le petit cube d'extraction un peu plus grand.
difference() {
// original
cube (size = [2,2,2]);
// objet qui extrait
# translate ([0.5,0.5,-0.5]) {
cube (size = [1,1,3]);
}
}
Intersection
La commande intersection créé l'intersection des tous les nœuds enfant. Cela garde toutes les proportions que cela chevauche.
Exemple:
intersection() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
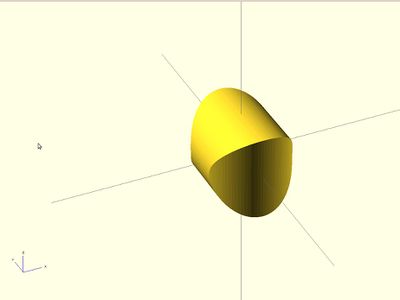
Modifier characters - aide pour composer
Aussi appelé modifier characters cela vous permet de mieux voir ce qu'il se passe. Si vous mettez un modifier characters avant une sous arborescence vous pouvez mieux comprendre ce que certains éléments du design font. C'est particulièrement le cas pour les opérations d'union (fusions), intersection et difference.
- # Modificateur de Debug
- L'arborescence sera rendue, mais il y aura aussi des formes dessinés en violet.
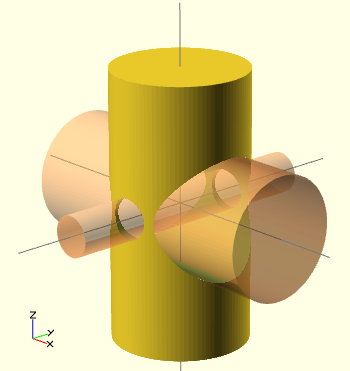
Code d'exemple:
difference() {
// objets de départ
cylinder (h = 4, r=1, center = true, $fn=100);
// premier objet qui sera soustrait
# rotate ([90,0,0]) cylinder (h = 4, r=0.3, center = true, $fn=100);
// deuxième objet qui sera soustrait
# rotate ([0,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
- % Modificateur Background
- Montre une arborescence dans le background. Les objets seront montrés en gris clair et les transformations seront appliquées, mais on ne les verra pas.
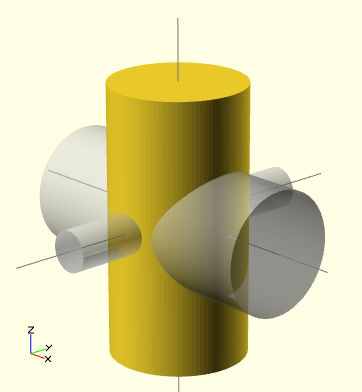
Exemple:
difference() {
// objets de départ
cylinder (h = 4, r=1, center = true, $fn=100);
// premier objet qui sera soustrait
% rotate ([90,0,0]) cylinder (h = 4, r=0.3, center = true, $fn=100);
// deuxième objet qui sera soustrait
% rotate ([0,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
- ! Modificateur Root
Le modificateur root va ignorer le reste du design et va utiliser son arborescence comme racine du design. C'est utile pour regarder seulement un élément, sans avoir besoin de copier/coller dans un fichier test.
Exemple: ! { ... }
- * Modificateur Disable
Le modificateur disable ignore simplement tout son arborescence. Cela a la même fonctionnalité que de commenter avec //. Exemple d'utilisation:
* { ... }
Exemples de CSG simples
L'opération suivante va couper une le bas d'une sphère de façon plate par son milieu.
difference() {
// Une sphère avec 5mm de rayon
# sphere(r=5, $fn=100);
// pousse 5mm vers le bas
translate(v=[0,0,-5]) {
//Le cube servant à couper
# cube(size = 10, center = true);
}
}
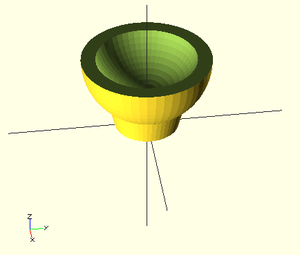
L'exemple suivant créé un simple petit bol.
// Résolution
$fn=50;
//Bouge le tout vers le haut
translate (v=[0,0,12]) {
difference() {
difference() {
// Sphère externe
sphere(r=10, $fn=50);
translate(v=[0,0,2]) {
//Sphère interne
sphere(r=8, $fn=50);
}
}
translate(v=[0,0,5]) {
// Cube servant à couper
cube(size = [20,20,10], center = true);
}
}
// Quelque chose pour porter le tout
translate(v=[0,0,-10]) {
cylinder (h=4, r1=5, r2=6, center = true);
}
}
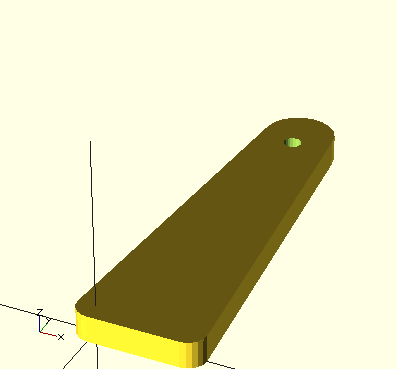
L'exemple suivant créé un simple porte-clés
$fn = 20;
difference () {
hull () {
# translate([0,0,0]) cylinder(r=2,h=3);
translate([10,0,0]) cylinder(r=2,h=3);
translate([5,40,0]) cylinder(r=4,h=3);
}
translate([5,38,-1]) cylinder(r=1,h=5);
}
Voir aussi: Doblo factory, le seul grand projet que nous avons tenté avec OpenScad.