OpenScad beginners tutorial

The educational technology and digital learning wiki
Jump to navigation Jump to search

Introduction

“OpenSCAD is a software for creating solid 3D CAD objects. It is free software and available for Linux/UNIX, MS Windows and Apples OS X. Unlike most free software for creating 3D models (such as the famous application Blender) it does not focus on the artistic aspects of 3D modelling but instead on the CAD aspects. Thus it might be the application you are looking for when you are planning to create 3D models of machine parts but pretty sure is not what you are looking for when you are more interested in creating computer-animated movies. OpenSCAD is not an interactive modeller. Instead it is something like a 3D-compiler that reads in a script file that describes the object and renders the 3D model from this script file (see examples below). This gives you (the designer) full control over the modelling process and enables you to easily change any step in the modelling process or make designes that are defined by configurable parameters.” (http://openscad.org/, retrieved 22:58, 17 March 2010 (UTC)

OpenScad should run on most computers. However a good CPU and a good graphics card help. If OpenScad models are too slow, try to cut down triangles in circles. In that respect, see the $fa, $fs and $fn special variables explained below.

See also:

Creating our first model and the interface

This section shorly explains how to use OpenScad and its programming interface.

First model

For our first model we will create a simple 2 x 3 x 4 cuboid. In the openScad editor type the following one-line command: 

cube([2,3,4]);

This will define a simple cube of size x=2, y=3 and z=4.

Cube

The cuboid can now be compiled and rendered as we shall show below.

The software - compiling scad code

The Interface looks like this:

  • To the left an editing window. Of course you could use an external editor, e.g. I use emacs because it can format (use c-mode or install an openscad mode)
  • To the right the rendering window.
Screenshot of OpenScad 2010.03.08
To open a .scad file
  • menu: File->Open
To compile (see the result)
  • menu: Design->Compile or F5
  • Use menu: Reload and compile or F4. If you prefer using an external editor for editing .scad code, the program will detect change of file date and automatically reload. I use emacs in order to get "real" indentation support and good syntax high-lighting).
To render for real and to export
  1. menu: Design-> Compile and Render (CGAL) or F6 .... this can take many minutes. However, various parts are cached and the next rendering could be much faster.
  2. menu: Design-> Export as .STL
Once you compiled and rendered (CGAL)
  • You can view the CGAL grid only (Menu: View->CGAL Grid Only or F11)
The View Menu
  • Tick "Show Axis"
  • You may switch between "Open CSG" and "Thrown together" mode for looking at the result
  • Once an object is rendered (not just compiled), you may explore the other options. In the same menu you will find various option to look at compiled or compiled + rendered models. Explore these and remember some shortcuts.

Some 3D principles

It's good to understand some of the 3D terminology, in order to be able to follow instruction or to figure out why things went wrong...

“The basic object used in mesh modelling is a vertex, a point in three dimensional space. Two vertices connected by a straight line become an edge. Three vertices, connected to the each other by three edges, define a triangle, which is the simplest polygon (face) in Euclidean space. More complex polygons can be created out of multiple triangles, or as a single object with more than 3 vertices. Four sided polygons (generally referred to as quads) and triangles are the most common shapes used in polygonal modeling. A group of polygons, connected to each other by shared vertices, is generally referred to as an element. Each of the polygons making up an element is called a face.” (Polygonal modeling, Wikipedia))

“In geometry, a vertex (plural vertices) is a special kind of point which describes the corners or intersections of geometric shapes. Vertices are commonly used in computer graphics to define the corners of surfaces (typically triangles) in 3D models, where each such point is given as a vector. A vertex of a polygon is the point of intersection of two edges, a vertex of a polyhedron is the point of intersection of three or more edges or face.” Vertex geometry, Wikipedia, retrieved 17:25, 23 March 2010 (UTC)

The faces or facets define the surface of a 3-dimensional object, i.e. what is between "outside" and "inside".

“Many modeling programs do not strictly enforce geometric theory; for example, it is possible for two vertices to have two distinct edges connecting them, occupying the exact same spatial location. It is also possible for two vertices to exist at the same spatial coordinates, or two faces to exist at the same location. Situations such as these are usually not desired and many packages support an auto-cleanup function. If auto-cleanup is not present, however, they must be deleted manually.” Vertex geometry, Wikipedia, retrieved 17:25, 23 March 2010 (UTC)

“A group of polygons which are connected together by shared vertices is referred to as a mesh. In order for a mesh to appear attractive when rendered, it is desirable that it be non-self-intersecting, meaning that no edge passes through a polygon. Another way of looking at this is that the mesh cannot pierce itself. It is also desirable that the mesh not contain any errors such as doubled vertices, edges, or faces. For some purposes it is important that the mesh be a manifold – that is, that it does not contain holes or singularities (locations where two distinct sections of the mesh are connected by a single vertex).” Vertex geometry, Wikipedia, retrieved 17:25, 23 March 2010 (UTC)

In many formats, e.g. STL and OpenSCAD, the following principle applies: “(i) The normal and each vertex of every facet are specified by three coordinates each, so there is a total of 12 numbers stored for each facet. (ii) Each facet is part of the boundary between the interior and the exterior of the object. The orientation of the facets (which way is ``out and which way is ``in) is specified redundantly in two ways which must be consistent. First, the direction of the normal is outward. Second, the vertices are listed in counterclockwise order when looking at the object from the outside (right-hand rule). (iii) Each triangle must share two vertices with each of its adjacent triangles. This is known as vertex-to-vertex rule. (iv) The object represented must be located in the all-positive octant (all vertex coordinates must be positive).” (Daniel Rypl, Zdenek Bittnar, 2004, retrieved April 2010.

The normal or surface normal is a vector that is perpendicular to a face. Surface normal, Wikipedia, retrieved 15:07, 20 November 2011 (UTC)

Example code

Using existing models

It is best to learn first how to use ready-made OpenScad modules. Download from a place like thingverse.

Most of these files define modules (aka functions) that you just can execute with or without parameters in order to render a model.

Modules without parameters:

The door stopper examples which you can download as thing 2154 from thingiverse are defined as two modules in a single *.scad file, door-stopper-2.scad. Download, or copy/paste the code from here. Of course, these door stopper modules actually can be parametrized, but it's done with variables as you can see.

Modules with parameters:

The parametric Lego/Duplo block on the other hand (thing 2014) does include parameters, e.g. you could call it like this for a small 2x2x3 brick with nibbles. 

duplo(1,1,3,true);

or like this for a larger brick without nibbles. 

duplo(2,2,4,false);

Just try: compile and change the parameters if they don't suit you. We also created a more sophisticated doblo factory that also may study.

Modules with named parameters:

You also can use parameter names as opposed to just using positions. The following example would with doblo factory. 

doblo   (col=0,  
         row=4, 
         up=0,  
	 width=4, 
         length=2, 
         height=FULL, 
	 nibbles_on_off=true, 
         diamonds_on_off=false,
	 scale=LUGO);

If default parameters are defined, you just could type 

doblo ();

in order to get a 4x2 full height typical Lego-compatible brick done.

If you prefer to learn more about OpenScad before trying, skip these examples and come back later.

Simple door stopper

The following code will create a doorstopper. Instead of trying to figure out this example, you also could skip it and read the rest of this article first.

To use this module you will have to add the following line to the code. I.e. it will call the "door_stopper_simple" module: 

 door_stopper_simple ();

// To use it, uncomment
// door_stopper_simple ();

module door_stopper_simple ()
{
    height = 20  ;
    length = 125 ;
    width= 40 ;
    half_width  = width / 2;
    
    borders = 10; // 1 cm on each side

    top_cube_length = length - 4 * borders;
    top_cube_width  = width - 2 * borders;
    top_cube_height = height ;  // make it big enough
    top_z = height/2 + 4 ; // adjust manually ;)

    tip_cut_pos = length/2 - 0.5;

    difference() {
	translate ([-length/2.0, 0, 0]) {
    	    polyhedron (	
	    		points = [[0, -half_width, height], [0, half_width, height], [0, half_width, 0], [0, -half_width, 0], [length, -half_width, 0], [length, half_width, 0]],
			triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5],  [5,2,4], [4,2,3], ]);
	}

	// top inset
	translate ([-1 * borders, 0, top_z]) {
	    # cube ([top_cube_length,
		     top_cube_width,
		     top_cube_height],
		    center=true) ;
	}
	// cut of the tip a bit

	translate ([tip_cut_pos, 0, 0]) {
	    # cube ([20,
		     width + 1,
		     height],
		    center=true) ;
	}
    }
}

Door stopper

The following model is a bit more sophisticated.

To use it: door_stopper (); 

// To use it, uncomment
// door_stopper ();

module door_stopper ()
{
    height = 25  ;
    length = 120 ;
    width= 60 ;
    half_width  = width / 2;
    
    borders = 10; // 1 cm on each side

    // params for bottom inset
    bottom_cube_length = length - 4 * borders;
    bottom_cube_width = width - 2 * borders;
    bottom_cube_height = 6.0 ; // 3mm in / 3mm outsite
    bottom_z = 0;

    // params for top inset
    top_cube_length = length - 4 * borders;
    top_cube_width  = width - 2 * borders;
    top_cube_height = height ;  // make it big enough // 25
    top_z = height/2 + 7.5 ; //  12.5 + 7.5 = 10 ; 10 - 2.5 = 7.5

    // param for tip
    tip_cut_pos = length/2 - 0.5;

    // param for top tip
    top_tip_pos = height + 0.5; 

    difference() {
	translate ([-length/2.0, 0, 0]) {
    	    polyhedron (	
	    		points = [[0, -half_width, height], [0, half_width, height], [0, half_width, 0], [0, -half_width, 0], [length, -half_width, 0], [length, half_width, 0]],
			triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5],  [5,2,4], [4,2,3], ]);
	}
	// bottom inset
	translate ([-1 * borders, 0, bottom_z]) {
	    # cube ([bottom_cube_length,
		     bottom_cube_width,
		     bottom_cube_height],
		    center=true) ;
	}
	// top inset
	translate ([-1 * borders, 0, top_z]) {
	    # cube ([top_cube_length,
		     top_cube_width,
		     top_cube_height],
		    center=true) ;
	}
	// cut of the top tip a bit
	translate ([- length/2 + 10, 0, top_tip_pos]) {
	    # cube ([length / 2,
		     width+2,
		     height / 2],
		    center=true) ;
	}
	// cut of the front tip a bit
	translate ([tip_cut_pos, 0, 0]) {
	    # cube ([20,
		   width + 1,
		   height],
		  center=true) ;
	}
    }	    
}


Door stopper model

You then also could add some text like this. I did that using netfabb Pro. It allows to create 3D text and to assemble various parts into a single .STL

Door stopper printed with PLA

Below is the printer result.

Door stopper printed with PLA

Parametric Lego Duplo block

This code is a derivative of the parametric lego duplo. It is the most complicated kind of OpenScad code we played with. Domonoky. We also uploaded it to Thingyverse. People with a good background in mathematics can get a lot more out of OpenScad .... 

//the duplo itself
// parameters are: 
// width: 1 =standard 4x4 duplo with.
// length: 1= standard 4x4 duplo length
// height: 1= minimal duplo height
// nibbles: true or false
 
duplo(1,1,3,true);


module duplo(width,length,height,nibbles) 
{
	//size definitions
	
	ns = 8.4;  //nibble start offset
	no = 6.53; //nibbleoffset
	nbo = 16; // nibble bottom offset
	
	duplowidth = 31.66;
	duplolength=31.66;
	duploheight=9.6;
	duplowall = 1.55;	
	
	
	//the cube
	difference() {
		cube([width*duplowidth,length*duplolength,height*duploheight],true);
		translate([0,0,-duplowall]) 	
			cube([width*duplowidth - 2*duplowall,length*duplolength-2*duplowall,height*duploheight],true);
	}

	//nibbles on top
         if  (nibbles)
     	   {
	    	for(j=[1:length])
		{
			for (i = [1:width])
			{
				translate([i*ns+(i-1)*no,j*ns+(j-1)*no,6.9+(height-1)*duploheight/2]) duplonibble();
				translate([i*-ns+(i-1)*-no,j*ns+(j-1)*no,6.9+(height-1)*duploheight/2]) duplonibble();
				translate([i*ns+(i-1)*no,j*-ns+(j-1)*-no,6.9+(height-1)*duploheight/2]) duplonibble();
				translate([i*-ns+(i-1)*-no,j*-ns+(j-1)*-no,6.9+(height-1)*duploheight/2]) duplonibble();
			}
		}
	        }

	//nibble bottom
	for(j=[1:length])
	{
		for (i = [1:width])
		{
			translate([(i-1)*nbo,(j-1)*nbo,0]) duplobottomnibble(height*duploheight);
			translate([(i-1)*-nbo,(j-1)*-nbo,0]) duplobottomnibble(height*duploheight);
			translate([(i-1)*-nbo,(j-1)*nbo,0]) duplobottomnibble(height*duploheight);
			translate([(i-1)*nbo,(j-1)*-nbo,0]) duplobottomnibble(height*duploheight);
		}
	}
	//little walls inside[http://www.thingiverse.com/Domonoky Domonoky]
	difference() 
	{
		union()
	 	{
			for(j=[1:length])
			{	
				for (i = [1:width])
				{
					translate([0,j*ns+(j-1)*no,0 ]) cube([width*duplowidth,1.35,height*duploheight],true);
					translate([0,j*-ns+(j-1)*-no,0 ]) cube([width*duplowidth,1.35,height*duploheight],true);
					translate([i*ns+(i-1)*no,0,0 ]) cube([1.35,length*duplolength,,height*duploheight],true);
					translate([i*-ns+(i-1)*-no,0,0 ]) cube([1.35,length*duplolength,height*duploheight],true);
				}
			}
		}
		cube([width*duplowidth - 4*duplowall,length*duplolength-4*duplowall,height*duploheight+2],true);
	}
}


module duplonibble()
{
	difference() {
		cylinder(r=4.7,h=4.5,center=true,$fs = 0.01);
		cylinder(r=3.4,h=5.5,center=true,$fs = 0.01);
	}
}

module duplobottomnibble(height)[http://www.thingiverse.com/Domonoky Domonoky]
{
	difference() {
		cylinder(r=6.6,h=height,center=true,$fs = 0.01);
		cylinder(r=5.3,h=height+1,center=true,$fs = 0.01);
	}

}

The OpenScad language

Modules

Modules can be roughly compared to functions, macros or sub-routines in another programming language. With modules you may define reusable code.

Example:

  • The module called "thing" is being called from a module called "demo_proj".

source: Example021.scad from the software distribution 

module thing()
{
	$fa = 30;
	difference() {
		sphere(r = 25);
		cylinder(h = 62.5, r1 = 12.5, r2 = 6.25, center = true);
		rotate(90, [ 1, 0, 0 ]) cylinder(h = 62.5,
				r1 = 12.5, r2 = 6.25, center = true);
		rotate(90, [ 0, 1, 0 ]) cylinder(h = 62.5,
				r1 = 12.5, r2 = 6.25, center = true);
	}
}

module demo_proj()
{
	linear_extrude(center = true, height = 0.5) projection(cut = false) thing();
	thing();
}

demo_proj();
  • Modules may be embedded within modules and can have arguments of course

Control flow

For Loop

For loop using a vector

Iterate over the values in a vector or range.

Syntax: 

for (loop_variable_name = range or vector) {
   .....
   }
Parameters
loop_variable_name = Name of the variable to use within the for loop.
range: [low : high]. Low and high can be either numbers of variables
vector: A vector like [1,2,10,40.5]
For loop using a range

Usage examples: A for loop using a vector 

for ( z = [-1, 1, -2.5]) {
 translate( [0, 0, z] ) 
    cube(size = 1, center = false);
}

A for loop using a range 

 for ( i = [0:5] ) {
  rotate( i*360/6, [1, 0, 0])
   translate( [0, 10, 0] ) sphere(r = 1);
 }

Intersection For Loop

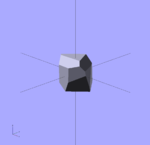
OpenScad Intersection-for loop (rotation)

Iterates over a vector of vectors, resulting in the intersection/overlap of all generated objects.

Syntax: 

intersection_for (loop_variable_name = vector_of_vectors) {
   .....
   }
Parameters
loop_variable_name = Name of the variable to use within the for loop.
vector_of_vectors: A vector like [ [1,2,10],[14,-20.3,40.5] ]

Usage example 1 - rotation : 

 intersection_for(i = [
 			[0, 0, 0],
 			[10, 20, 300],
 			[200, 40, 57],
 			[20, 88, 57]
 		])
 	rotate(i) cube([100, 20, 20], center = true);
OpenScad Intersection-for loop (translation). Note: to generate the left image add a # before the translation, this will display the outline of the generated volume before the intersection is take.

Usage example 2 - translation: 

 intersection_for(i = [
	[0, 0, 0],
	[2, 1, 1],
	[-2, 1, 0]
	])
	translate (i) cylinder(r=5, h=10, center = true);

If Statement

Conditionally evaluate a sub-tree.

Syntax 

if (boolean_expression) { .... }
if (boolean_expression) { .... } else {.... }
if (boolean_expression) { .... } else if (boolean_expression) {.... }
if (boolean_expression) { .... } else if (boolean_expression) {.... } else {....}

Parameters

  • The boolean expression that should be used as condition

Usage example 1: 

 if (x > y) {
  cube(size = 1, center = false);
 }

Usage example 2: 

SCALE = 0.5 ;
... other variables .....

module doblonibble() {
    // Lego size does not have holes in the nibbles
    if (SCALE < 0.6) {
	cylinder(r=NB_RADIUS, h=NH,  center=true,  $fs = 0.05);
    } else {
	difference() {
	    cylinder(r=NB_RADIUS,h=NH,  center=true,  $fs = 0.05);
	    cylinder(r=NB_RADIUS_INSIDE,h=NH+1,center=true, $fs = 0.05);
	}
    }
}

Variables and assign Statement

Variables

Variable assignments have the usual C-like syntax, e.g. 

SCALE = 1;

or 

PART_HEIGHT  = ((SCALE < 0.6) && LEGO_DIV) ? 3.2 * LEGO_SCALE : 4.8 * SCALE ;

However and don't forget this:

  • OpenSCAD calculates its variable values at compile-time, not run-time, the last variable assignment will apply everywhere the variable is used.
  • It may be helpful to think of them as overrideable constants rather than as variables. That means that you can set variables in some library and then override them in the file that will load the library. You cannot assign 2 different values to the same variable when you compute a model !

Assign

Set variables to a new value for a sub-tree. This can be used within a module to store intermediate values. In the example

Syntax: 

 assign (var1= expr1, var2= expr2, ....)

Example that demonstrates variables that are (re-)assigned: 

for (i = [10:50])
    assign (angle = i*360/20, distance = i*10, r = i*2) {
        rotate(angle, [1, 0, 0])
            translate( [0, distance, 0] ) sphere(r = r);
    }

The local "angle", "distance" and "r" variables are changed in each cycle of the loop.

Mathematical operators and functions

OpenSCAD operators seem to work like in other C-like languages. See the [ official manual] details:

Conditionals are also implemented. Example: 

condition ? if_true_expression : if_false_expression

Example: 

HEIGHT = (SCALE < 0.5) ? 3 : 6*1/1 ;
If SCALE==0.6, then HEIGHT will be 6. If it's smaller than 0.5 then HEIGHT==3

Functions

Can be used to define simple utility modules. Not to be confused with "modules"

Special variables

As explained in the OpenScad wiki book, variables starting with a '$' are special variables.

Notice for programmers: The semantic of special variables is similar to the special variables in lisp: they have dynamic instead of lexical scoping. What the means is that its values are defined at run time. E.g. let's assume that you start your code with $fa = 5, then call a module A within which you define $fa = 7. When this module A calls yet another module B, the second definition ($fa==7) will be used.

The $fa, $fs and $fn special variables control the number of facets used to generate an arc. As explained above, you can override these in each module:

$fa
is the angle of the fragments. It sets the minimum angle for a fragment. Even a huge circle does not have more fragments than 360 divided by this number. The default value is 12 (i.e. 30 fragments for a full circle).
$fs
is the size of the fragments and defines the minimum size of a fragment. Because of this variable very small circles have a smaller number of fragments then specified using $fa. The default value is 1.
$fn
is the number of fragments. It usually is 0. When this variable has a value greater than zero, the other two variables are ignored and full cirle is rendered using this number of fragments. The default value is 0.

The shape of a circle can be improved by setting one of the special parameters $fn, $fs, and $fa. When $fa and $fs are used to determine the number of fragments for a circle, then OpenSCAD will never use less than 5 fragments.

If you want to speed up rendering for testing, a good trick is to set facets to very low at the top of the script. Since $fn is a special variable, it will affect all objects, unless it is overridden.

Low resolution example 

$fn=10;

High resolution example 

$fn=100;

High resolution means many more triangles and more waiting :) Most often, 20-50 should be enough for 3D printing.

Primitive Solids

OpenScad has the "usual" primitives, e.g. cube, cylinder, sphere.

Coordinates are defined with some of array: E.g. [2,3,4] means x=2, y=3 and z=4.

Cube

Creates a cube at the origin of the coordinate system. When center is true the cube will be centered on the origin, otherwise it is created in the first octant. The argument names are optional if the arguments are given in the same order as specified in the parameters.

Parameters:

size
Decimal or 3 value array. If a single number is given, the result will be a cube with sides of that length. If a 3 value array is given, then the values will correspond to the lengths of the X, Y, and Z sides. Default value is 1.
center
Boolean. This determines the positioning of the object. If true, object is centered at (0,0,0). Otherwise, the cube is placed in the positive quadrant with one corner at (0,0,0). Defaults to false

Example 1: 

cube ([2,3,4])

Example 2: 

bottom_cube_length = 2;
bottom_cube_width = 3;
bottom_cube_height = 2;
cube ([bottom_cube_length,
	bottom_cube_width,
	bottom_cube_height],
	center=true) ;

Example 3: 

cube(size = 1, center = false);
cube(size = [1,2,3], center = true);
Two cube examples. Source: OpenSCAD User Manual/Primitive Solids

Sphere

Creates a sphere at the origin of the coordinate system. The argument name is optional.

Parameters
r
Decimal. This is the radius of the sphere. The resolution of the sphere will be based on the size of the sphere and the $fa, $fs and $fn special variables.

Usage Examples 

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);
sphere(2, $fn=100); // high resolution sphere with a 2mm radius
sphere(2, $fa=5, $fs=0.1); // 2mm (less) high resolution sphere
Three sphere examples. Source: OpenSCAD User Manual/Primitive Solids

Cylinder

Creates a cylinder at the origin of the coordinate system. When both radii are same it is also possible to specify a single radius using the argument name r. The argument names are optional if the arguments are given in the same order as specified above.

Parameters

h
Decimal. This is the height of the cylinder. Default value is 1.
r1
Decimal. This is the radius of the cylinder/cone on top end. Default value is 1.
r2
Decimal. This is the radius of the cylinder/cone on bottom end. Default value is 1.
r
Decimal. The radius of both top and bottom ends of the cylinder. Use this parameter if you want a non-cone shaped cylinder. Default value is 1.

Usage Examples 

cylinder(h = 10, r1 = 10, r2 = 20, center = false);
cylinder(h = 10, r1 = 20, r2 = 10, center = true);
cylinder(h = 10, r=20);
OpenScad spheres example. Source: OpenSCAD User Manual/Primitive Solids

Polyhedrons

Polyhedrons are the most difficult shapes to deal with. Instead of using this function, you could (a) think about how you could combine simple forms instead or (b) look at 2D extrusion.

  • A polyhedron (plural polyhedra or polyhedrons) is often defined as a geometric solid with flat faces and straight edges.(Wikipedia, retrieved 17:25, 23 March 2010 (UTC)).


Any polyhedron can be built up from different kinds of element or entity, each associated with a different number of dimensions:

  • 3 dimensions: The body is bounded by the faces, and is usually the volume enclosed by them.
  • 2 dimensions: A face is a polygon bounded by a circuit of edges, and usually including the flat (plane) region inside the boundary. These polygonal faces together make up the polyhedral surface.
  • 1 dimension: An edge joins one vertex to another and one face to another, and is usually a line segment. The edges together make up the polyhedral skeleton.
  • 0 dimensions: A vertex (plural vertices) is a corner point.
(Wikipedia, retrieved 17:25, 23 March 2010 (UTC)).

Syntax: 

polyhedron(points = [ [x, y, z], ... ], triangles = [ [p1, p2, p3..], ... ], convexity = N);

Create a polyhedron with the specified points and triangles. (The 'pN' components of the triangles vector are 0-indexed references to the elements of the points vector.)

Example (see picture below) 

polyhedron ( points = [[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60]], 
triangles = [[0,3,2], [0,2,1], [3,0,4], [1,2,5], [0,5,4], [0,1,5],  [5,2,4], [4,2,3], ]);
A simple hand-crafted Polyhedron

Note that OpenSCAD currently crashes if your polygons are not all oriented the same way; pay attention to the vertex ordering (don't understand this !) e.g. 

  polyhedron(points=[[0,0,0],[100,0,0],[0,100,0],[0,100,100]], triangles=[[0,1,2],[0,1,3],[0,2,3],[1,2,3]]); //Crashes
  polyhedron(points=[[0,0,0],[100,0,0],[0,100,0],[0,100,100]], triangles=[[0,1,2],[1,0,3],[0,2,3],[2,1,3]]); //Works

An other example:

A hand-crafted Polyhedron

Let's now see how to fix polyhedrons with badly oriented polygons. When you select 'Thrown together' from the view menu and compile the design (not compile and render!) you will see a preview with the mis-oriented polygons highlighted. Unfortunately this highlighting is not possible in the OpenCSG preview mode because it would interfere with the way the OpenCSG preview mode is implemented.)

Below you can see such a problematic polyhedron, bad triangles are in pink. 

// Bad polyhedron
polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     triangles = [
		  [0,2,3],   [0,1,2],  [0,4,5],  [0,5,1],   [5,4,2],  [2,4,3],
                  [6,8,9],  [6,7,8],  [6,10,11], [6,11,7], [10,8,11],
		  [10,9,8], [0,3,9],  [9,0,6], [10,6, 0],  [0,4,10],
                  [3,9,10], [3,10,4], [1,7,11],  [1,11,5], [1,7,8],  
                  [1,8,2],  [2,8,11], [2,11,5]
		  ]
     );
Polyhedron with badly oriented polygons

A correct polyhedron would be the following: 

polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     triangles = [
		  [0,3,2],  [0,2,1],  [4,0,5],  [5,0,1],  [5,2,4],  [4,2,3],
                  [6,8,9],  [6,7,8],  [6,10,11],[6,11,7], [10,8,11],
		  [10,9,8], [3,0,9],  [9,0,6],  [10,6, 0],[0,4,10],
                  [3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],  
                  [2,8,1],  [8,2,11], [5,11,2]
		  ]
     );

Beginner's tip: If you don't really understand "orientation", then just identify the mis-oriented pink triangles and then permute the corresponding triangle's order of vertices until you get it right. E.g. in the above example, the third triangle vector (i.e. number 2, [0,4,5]) was wrong and we fixed it as [4,0,5]. In addition you may select "Show Edges" from the "View Menu", make a screen capture, print it and number both the vertices (points) and the triangles. In our example, the points are in black and the triangles in blue. Then, turn the picture around and make a second copy from the back if needed.

Polyhedron with badly oriented polygons

Transformations

scale

Scales its child elements using the specified vector. The argument name v is optional.

Syntax
scale(v = [x, y, z]) { ... }
Example
Create an oval of length = 40 in the x direction; x and z remain the same.
 scale (v=[2,1,1]) cylinder(h = 10, r=20);

rotate

Rotate accepts several versions of arguments.

Syntax for 2D rotation around the Z-axis
rotate (deg)

Example:

rotate(45) square(10);
Syntax for rotations about 1 or more axis
rotate(a = deg, v = [x, y, z]) { ... }

Rotates its child a degrees around the specified vector v rooted in the origin of the coordinate system.

Parameters:

a
Degrees
v
An array of [x,y,z]

Example: rotates the object produced by module 8bit_char by 270 degrees around the z asis. 

rotate (a=270, v=[0,0,1]) {
   8bit_char(char, size_mm, height);
}
Alternative syntax
rotate(a = [deg_x,deg_y,deg_z] { ... }

Parameters:

a
Vector of three degrees. In this case the child nodes are rotated around the positive x, y and z axis (in this order) by the specified number of degrees.

For example, to flip an object upside-down, you might do this: 

rotate(a=[0,180,0]) { ... }

Notice: Argument names are optional if the arguments are given in the same order as specified above.

translate

Syntax
translate(v = [x, y, z]) { ... }

Translates (moves) its child elements along the specified vector. The argument name is optional, i.e. the following also works:

translate([x, y, z]) { ... }

mirror

Mirror operation ([1,0,0] of a Lego Brick (original to the right)
Syntax
mirror([ 1, 0, 0 ]) { ... }

Mirrors the child element on a plane through the origin. The argument to mirror() is the normal vector on that plane. 

translate ([-100,0,0]) import("motivation.stl");

color ("red") {
  mirror ([1,0,0]) {
    translate ([-100,0,0]) import("motivation.stl");
  }	 
};
Mirror operations of a Lego Brick (original = grey to the right)

Imagine a orthogonal plane to the X axis that goes through the origin. This will be the mirror. 

translate ([-100,0,0]) import("motivation.stl");

color ("red") {
  mirror ([1,0,0]) {
    translate ([-100,0,0]) import("motivation.stl");
  }	 
};


color ("blue") {
  mirror ([0,1,0]) {
    translate ([-100,0,0]) import("motivation.stl");
  }
};	 

color ("cyan") {
  mirror ([1,1,0]) {
    translate ([-100,0,0]) import("motivation.stl");
  }
};	 


color ("yellow") {
  mirror ([0,0,1]) {
    translate ([-100,0,0]) import("motivation.stl");
  }
};	 
  
color ("magenta") {
  mirror ([0,1,1]) {
    translate ([-100,0,0]) import("motivation.stl");
  }
};	 

color ("green") {
  mirror ([1,1,1]) {
    translate ([-100,0,0]) import("motivation.stl");
  }
};

multmatrix

Syntax
multmatrix(m = [...]) { ... }

Example (translates by [10, 20, 30]): 

 multmatrix(m = [ [1, 0, 0, 10],
                  [0, 1, 0, 20],
                  [0, 0, 1, 30],
                  [0, 0, 0,  1]
                ]) cylinder();

Multiplies the geometry of all child elements with the given 4x4 transformation matrix.

color

Usage example:
color([r, g, b, a]) { ... }

Displays the child elements using the specified RGB color + alpha value. This is only used for the OpenCSG and Thrown Together display modes. The alpha value will default to 1.0 (opaque) if not specified.

NB! The r, g, b, a values are limited to floating point values in the range { 0.0 ... 1.0 } rather than the more traditional integers { 0 ... 255 }. However you can specify the values as fractions, e.g. for R,G,B integers in {0 ... 255} you can use: 

color([ R/255, G/255, B/255 ]) { ... }

If you need just simple colors, use something like (all CSS2/X11 colors should do): 

 color("red") cube () ;

See the CSS3 color names table

minkowski

Minkowski sums allow to add every element of A to every element of B. Not easy to understand and you also may read minkowski sum at cgal.org.


From the OpenScad Manual: 

$fn=50;
minkowski() {
    cube([10,10,2]);
    // rounded corners
    cylinder(r=2,h=2);
}
Rounding corner edges with Minkowski sum

To get rounded edges all over, once could use a sphere.

If you set $fn=50, it will take ages to compute 

$fn=20;
minkowski() {
  cube([10,10,2]);
  // rounded corners
  sphere(2);
}
Rounding all edges with Minkowski sum

Inside a Minkowski clause, transformations do not seem to work (May 2012).

hull

hull will create a hull from all objects that are inside. Read convex hull at cgal.org if you want to understand the principle. 

$fn = 20;
hull () {
  # translate([0,0,0]) cylinder(r=2,h=2);
  translate([10,0,0]) cylinder(r=2,h=2);
  translate([5,10,0]) cylinder(r=2,h=2);
}
Rounded triangle created with hull

CSG Modelling

Principle

CSG stands for Constructive solid geometry.

It is possible to create complex 3D models by combining simple 3D primitive objects, such as cubes, cylinders or spheres.

Merging of objects

The result of union will be "baked", i.e. if you stack up cubes aligned against each other, the result will be one shape (no internal walls). This is ideal behavior for rapman printing. Note however, that juxtaposition of objects can go badly wrong, e.g. two cubes cannot share a single edge as explained later.

Example 1: 

 union() {
   translate(0,0,x) import_stl("duck.stl");
   duplo(2,2,1.5,false);
 }

Example 2 (see the picture below) 

union() {
	cylinder (h = 4, r=1, center = true, $fn=100);
	rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Union of two cylinders - source: OpenSCAD User Manual/CSG Modelling

Difference

Difference substracts the 2nd (and all further) child nodes from the first one.

Example 1: 

difference() {
	cylinder (h = 4, r=1, center = true, $fn=100);
	rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Difference of two cylinders - source: OpenSCAD User Manual/CSG Modelling

Example 2: 

difference() {
	// start objects
	cylinder (h = 4, r=1, center = true, $fn=100);
        // first object that will substracted
	rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
        // second object that will be substracted
	rotate ([90,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}

You always should make sure that the extracting object is "longer" or "shorter" than the object from which you carve out. Else you can run into "object is not 2-manifold problems" described in the troubleshooting section.

"Manifold" means that it is "water tight" and that there are no holes in the geometry. In a valid 2-manifold each edge must connect exactly two facets. That means that the program must be able to connect a face with an object. E.g. if you use a cube of height 10 to carve out something from a wider of cube of height 10, it is not clear to which cube the top or the bottom belongs. So make the small "extracting" cube a bit longer: 

difference() {
	// original
	cube (size = [2,2,2]);
	// object that carves out
	# translate ([0.5,0.5,-0.5]) {
	    cube (size = [1,1,3]);	
	}
}
Correct use of difference

Intersection

Intersection creates the intersection of all child nodes. This keeps all the portions that overlap

Example: 

intersection() {
	cylinder (h = 4, r=1, center = true, $fn=100);
	rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Intersection of two cylinders - source: OpenSCAD User Manual/CSG Modelling

Modifier characters - help for composing

So-called modifier characters allow you better see what is going on. If you put one of these before a subtree you can better understand what certain design elements do (this is particularly the case for union, intersection and difference operations.

# Debug modifier
  • The subtree will be rendered, but it also will be drawn in transparent pink

Example code: 

difference() {
	// start objects
	cylinder (h = 4, r=1, center = true, $fn=100);
        // first object that will substracted
	# rotate ([90,0,0]) cylinder (h = 4, r=0.3, center = true, $fn=100);
        // second object that will be substracted
	# rotate ([0,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Debug Modifier example
% Background modifier
  • Show a subtree in the background. Objects will be shown in light gray and transformations applied, but the tree will not be rendered.

Example: 

difference() {
	// start objects
	cylinder (h = 4, r=1, center = true, $fn=100);
        // first object that will substracted
	% rotate ([90,0,0]) cylinder (h = 4, r=0.3, center = true, $fn=100);
        // second object that will be substracted
	% rotate ([0,90,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
Background modifier example
! Root modifier

Will ignore the rest of the design and use this subtree as design root. Useful to have a look a single element, without having to copy/paste it to a smaller test file.

Example: ! { ... }

* Disable Modifier

Simply ignores this entire subtree. Same function as commenting out with // Usage example: 

* { ... }

Simple CSG examples

The following operation will cut a Ball in half, flat side on bottom. 

difference() {
  // A ball with a 5mm radius
  # sphere(r=5, $fn=100); 
  // push 5mm downwards
  translate(v=[0,0,-5]) {
    //The cube for cutting 
    # cube(size = 10, center = true);
   }
}
Solid dome

The following creates a simple small bowl.

Simple 2cm x 2cm x 2cm+2mm bowl
// Resolution
$fn=50;

//Move the hole thing up
translate (v=[0,0,12]) {

  difference() {
    difference() {
      // Outer Ball
      sphere(r=10, $fn=50); 
      translate(v=[0,0,2]) {
	//Inner Ball
	sphere(r=8, $fn=50); 
      }
    }
    translate(v=[0,0,5]) {
      // Cutting cube
      cube(size = [20,20,10], center = true);
    }
  }
  // Something to sit on
  translate(v=[0,0,-10]) {
    cylinder (h=4, r1=5, r2=6, center = true);	
  }
}

The following creates a simple keyholder 

$fn = 20;
difference () {
hull () {
  # translate([0,0,0]) cylinder(r=2,h=3);
  translate([10,0,0]) cylinder(r=2,h=3);
  translate([5,40,0]) cylinder(r=4,h=3);
}
  translate([5,38,-1]) cylinder(r=1,h=5);
}
Keyholder made with hull (3 Cylinders) and a Cylinder to punch a hole

See also: Doblo factory, the only bigger project we attempted with OpenScad

2D geometry and linear extrusion

Extruding 2D shapes into 3D shapes is - besides CSG modeling - the other way to create complex objects. There exist several possibilities and combinations:

  • Type of extrusion: linear (including option torsion) and rotation (the 2D drawing is flipped 90 degrees and then extruded around the Z-axis
  • Source: Built-in 2D graphis (circle, square, ellipse, regular polygones made from circles with $fn set, and polygons,


Polygons

Polygones can have zero, one or several holes inside.

Example without hole that could be used to define the shape of some sofa walls: 

color ("red") linear_extrude (height=19.2)
polygon(points=[[0,0],[16,0],
		[16,32],[80,32],[80,0],
		[96,0], [96,48],[0,48]
	     ]);
Polygon example without hole (The picture includes a Doblo factory brick for reference


Example code with one hole 

polygon(points=[[0,0],[100,0],[0,100],[15,15],[65,15],[15,65]], paths=[[0,1,2],[3,4,5]]);
Polygon example with one hole

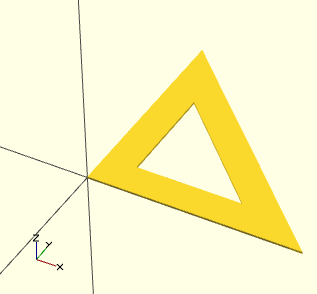
In this example, we have exactly 6 points (three for the "outer" triangle, and three for the "inner" one). Then, we connect each with two 2 path. In plain English, each element of a path must correspond to the position of a point defined in the points vector, e.g. "1" refers to [100,0].

Linear 2D to 3D extrusion from builtin 2D shapes

From any 2D graphic we can extract 3D shapes. Let's look at polygones.

Example: Simple polygone 

color ("lightblue") linear_extrude (height=19.2)
#polygon(points=[[0,0],[16,0],
		[16,32],[80,32],[80,0],
		[96,0], [96,48],[0,48]
	     ]);
Extruded polygon example. The Lego in the picture was made with doblo factory and is just included for size reference

Example: Polygone with a hole 

linear_extrude(height = 16, center = true, convexity = 10, twist = 0)
polygon(points=[[0,0],[100,0],[0,100],[15,15],[65,15],[15,65]], paths=[[0,1,2],[3,4,5]]);

Result: A 16mm high flat triangle with an empty triangle inside

Extruded polygon example

Example: Extrusion from CSG created 2D shapes

You also can create 2D shapes with CSG. E.g. you could create a kind of a moon shape by substracting a circle from a circle like this: 

difference () {
     circle (r=10);
     translate ([2,0,0]) circle(r=10);
}

A fuller example that includes some parameters is below: 

module half_moon (color="orange", size=16, thickness=4, fullness=0.5) {
     color (color)
	  rotate (a=[90,0,0])
	  linear_extrude (height=thickness)
	  difference () {
	  circle (r=size, $fs=0.2);
	  translate ([size*2*fullness,0,0]) {
	       circle (r=size,$fs=0.2);
	  }
     }
}

module moons () {
     half_moon(size=20,fullness=0.1,color="yellow");
     translate ([20,10,10]) half_moon(size=20,fullness=0.3,color="lightblue");
     translate ([40,20,20]) half_moon(size=10,fullness=0.5,color="red");
     }

moons ();
Extruded polygon from 2D CSG moon

Import and extrude 2D graphics from SVG

This section needs to be updated. It is not longer necessary to flatten Bezier curves and to export to DXF - Daniel K. Schneider (talk)

You can import two types of SVG objects

  • Closed polygone fills
  • Lines, but these will be translated to shapes

That means for example, that fonts have to be transformed to paths

According to the manual, OpenSCAD handles only closed polygons, so importing lines or open polygons is not possible. Instead open polygons are treated as shapes defined by their stroke-width. “Closed shapes ignore fill and stroke-width, open path use stroke width to generate the outline of the shape.”

Closed shapes are always using the geometric specification regardless of fill or stroke-with defined in the SVG file as the following picture copied from the manual shows:

  • SVG in Inkscape

    SVG in Inkscape

  • Imported into OpenSCAD

    Imported into OpenSCAD

Example: 

		    scale ([d_scale,d_scale,1]) 
		    linear_extrude(height = d_height, center = true, convexity = 10)
		    import (file = "test.svg");

See also:

Legacy procedure - Transforming and SVG file to a usable DXF file with Inkscape

This explains how to do it with an older OpenScad version (to be removed once we have done an example)

Lego-compatible Hamburger printed with 2 colors in PLA with a Felix Pro 1

Linear extrusion from imported graphics is a bit more tricky, since we will have to start from a well made DXF file. Since available clipart is in SVG we will start from there, according to the instructions by Nudel (thanks!).

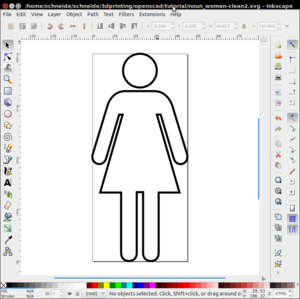
Finding some clip art

Let's create a 2D1/2 person, e.g. the kind one could find in certain platform games. There are two places with a good choice of SVG clipart.

With some search on Nounproject we found this women, a "public domain" icon.

  • In order to download a file, you will have to register. For most icons, there is a public and a pay version. I you decide to use the public version, you will have to give credits to the author. We do this by inserting a comment in the scad file and here.
  • Take the svg version. We renamed it to noun_woman.svg

This involves several steps. Basically, we have to transform the drawing into a a series of closed connected "path definitions", where a path is composed of straight lines (and not curves).

(1) Open the SVG in Inkscape and clean it

  • Fit the document size to the picture size: Menu File->Document Properties.
  • In the Custom size panel, open Resize page to content, then click Resize page to drawing or selection
  • Remove unused DEF's: File->Vacuum Defs.
  • Optimize SVG: File -> Save as... -> Optimized SVG.
  • File -> Save as ... -> Plain SVG

(2) Ungroup and remove the fill from the surfaces

  • Ungroup everything (Hit SHIFT CTRL-G)
  • Select all objects (CTRL-A)
  • Add some stroke color if needed. Hit SHIFT CTRL-F
  • Just in this case (fills are OK): Untick fill paint. Tick stroke paint (and select a color if necessary).

The result should look like this:

Cleaned SVG

(3) If necessary, move all layers to a single one. Kill the others.

(4) Translate all objects to paths

  • Select the object(s) and union iff the object is simple. Otherwise, I suggest creating a separate path for each part of the objects that should be filled
Menu Path -> Union
  • Select the remaining object and make it to path. You also could simplify it (before adding points again for creating a straight lines model)
Menu Path->Object to Path. Now it's a single path, event if it represents visually more than one drawing. I suggest to do some node surgery later.
  • Simplify if you can
Menu Path->Simplify.
  • Check if there are no other types of objects left

Open the XML editor (Menu Edit->XML Editor). Make sure that there are no other objects left.

(5) Replace the splines (curves) by straight lines.

  • Hit F2 (Edit path by nodes) to check if you need more nodes
  • Select all nodes (e.g. click on some node, then press CTRL-A)
  • Add more nodes if necessary: Click Insert new nodes into selected segments (left most icon on top).
  • Click Make segmented segments lines

Alternatively (and better in most cases):

  • Select each path and transform Bezier curves to series of straight lines with an extension
    • Use Extensions -> Modify Path -> Flatten Beziers before save as to Desktop Cutting Plotter (dxf).
    • Enter a low value, e.g. 0.2 for a smaller icon

Repeat this procedure for other path in the drawing.

(6) Optional: Do some path surgery. If you need to join two path:

  • Select two nodes from one path, Break path at selected nodes
  • Do the same with the other path
  • Delete maybe some points (select and hit "DEL")
  • Join two nodes (twice), using Join selected nodes
Join nodes

(6) Change the graphics (optional)

  • e.g. we made a nice skirt ...
  • In case you make changes (e.g. drag a node) make straight lines again !

(6) Save as DXF

  • File -> Save as; Select DXF
  • Untick everything

Once you got a clean DXF you can import the graphics and extrude 

color ("pink") linear_extrude(height = 5, center = true, convexity = 10)
import (file = "noun_woman-clean.dxf");
Pink SVG women extruded

Getting a more complex drawing to import is more tedious, since one might want to process each separate (not connected) subpath, as opposed to create a union and then translate all strokes.

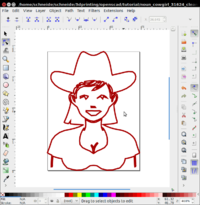
  • Cowgirl processed
  • Original cowgirl by Simon Child

    Original cowgirl by Simon Child

  • Simplified cowgirl (Simplified drawing, removed nodes, selected subpath, added nodes, transformed to straight lines (except some of the hair)

    Simplified cowgirl (Simplified drawing, removed nodes, selected subpath, added nodes, transformed to straight lines (except some of the hair)

  • Simplified cowgirl imported and extruded

    Simplified cowgirl imported and extruded

This object could be put on top of a Lego block or be substracted from one.

Cowgirl Lego-compatible bricks (see doblo factory)
Cleaned R2-D2 from Lluis Pareras on Nounproject

If nothing shows

  • Check if you really translated all segments to lines. Again, if you "union" your paths, then you can do all in one
  • Check if there is Adobe code inside the SVG. If there is, manually (with a text editor) get rid of it (after simplifying and optimizing and unionizing). A good example is R2-D2 from Luis Pararas. Only after radically removing everything except the path it would work. I did not investigate why. Actually it just could be the switch statement.

Creating 3D text

Extruded 2D text

Since version 2015.03 (March 2015), OpenScad has a text module that can produce 2D text that then can be extruded. It works "as is" on Windows. As of March 2015, I did not test Linux (Ubuntu), since I'd have to install the new version manually.

The text function accepts several arguments among which are:

  • size (the approximate font height)
  • font, the font name internal to OpenScad. You can get the list under the "help" menu.
  • halign and valign
  • spacing, for spacing out letters (probably a good idea when using a filament printer)

Simple example to create a text: 

 text("Text rocks")
Extruded 2D text using a Windows Wingdings font

3D text example: 

content = "Text rocks";
font = "Liberation Sans";

translate ([-30,0,0]) {
   linear_extrude(height = 3) {
       text(content, font = font, size = 10);
     }
 }

The example below says that spiders like their net and uses Windows Wingdings. Unfortunately it probably is not easily portable. Windows fonts can be installed, but it's work. 

content = "!Y\"";
font = "Webdings";

linear_extrude(height = 3) {
       text(content, font = font, spacing= 1.2, size = 10);
}

2D DXF drawings extracted from 3D STL shapes

From Giles BathGate, (retrieved dec 28 2010) 

projection(cut=false) import_stl(“/full/path/to/stl”);

or 

projection(cut=true) translate([0,0,-10]) rotate([0,90,0]) import_stl(“file.stl”);

Then, "export as" DXF: From the Design pull down menu choose Export as DXF.

Troubleshooting

Tracing

Echo Statements

This function echoes the contents to the compilation window. Useful for debugging code

Usage examples: 

my_h=50;
my_r=100;
echo("This is a cylinder with h=", my_h, " and r=", my_r);
cylinder(h=my_h, r=my_r);

Not simple objects

After compile and render GGAL (F6), you may see something like: 

Parsing design (AST generation)...
Compiling design (CSG Tree generation)...
Compilation finished.
Rendering Polygon Mesh using CGAL...
Number of vertices currently in CGAL cache: 600
Number of objects currently in CGAL cache: 3
   Top level object is a 3D object:
   Simple:        '''no'''
   Valid:         yes
   Vertices:      200

Then when you try to export to .STL you get a message like: 

Object isn't a valid 2-manifold! Modify your design..

In a valid 2-manifold each edge must connect extactly two facets. Here is a little example taken from the OpenSCAD Forum (retrieved 18:47, 22 March 2010 (UTC)): 

	module example1() {
		cube([20, 20, 20]);
		translate([-20, -20, 0]) cube([20, 20, 20]);
		cube([50, 50, 5], center = true);
	}

This example1 module is not a valid 2-manifold because both cubes are sharing one edge. They touch each other but do not intersect.

A not valid 2-manifold cube (simple = no)

The example2 module below would define a valid 2-manifold because there is an intersection (i.e. the cubes overlap a tiny bit). Now, each edge connects exactly two facets and the 2-manifold constraint is met. 

	module example2() {
		cube([20.1, 20.1, 20]);
		translate([-20, -20, 0]) cube([20.1, 20.1, 20]);
		cube([50, 50, 5], center = true);
	}

So, when performing composite solid geometry operations, it is important to remember that the piece you are subtracting must extend past the original part. (OpenSCAD Tip: Manifold Space and Time, retrieved 18:47, 22 March 2010 (UTC)).

Thingiverse Customizer

Allows to create OpenScad files that will allow users to parametrize. You will have to respect a few rules that are explained in the documentation.

Example code fragment: 

/* [Running/Walking] */
RunningDistance=2; //[2:100]
RunningDuration=5; //[10:600]
/* [Dimensions] */
CutAway=0.5; //[0.5,0.7,0.8,1,1.5,2,3,4]]
HoleDiameter=3; //[1:5]
ScaleFactor=1; //[0.5,1,1.5,2,2.5,3]

/* [Hidden] */
$fn = 100; //sets the smoothness of the whole

Links

Tutorials

Other stuff

In education

  • 3D Printed Science Projects, Ideas for your classroom, science fair or home. By Joan Horvath , Rich Cameron. Cheap e-book/print book from APress. Includes downloadable code.

Thingiverse Customizer

Geometric forms / 3D models

Software

OpenScad
Utilities
  • Inkscape to OpenSCAD converter v2. Inkscape extension to export Inkscape paths to OpenSCAD. This extension handles SVG arcs, clones, circles, ellipses, groups, lines, paths, polygons, polylines, rects, and splines. It also follows document transforms as well as viewports. Either an entire document or just the selected portions of a document are processed.
  • svgto3d Get a list of svg files and convert them to prepared scad designs. You'll then have to modify only the size. This is a read-to-go bash script for Linux/Unix. (to get this work on Win/Mac etc., installation work may be required ....). Under Debian/Ubuntu, you may need to: sudo apt-get install pstoedit

Alternatives to OpenSCAD

Credits and copyright modification

  • Parts of this article were taken from OpenSCAD User Manual
  • Note: By default, pictures were originally mine. Concurrently to writing this piece, I made updates to the manual on Wikibooks. Else, pictures are taken from the OpenSCAD Manual and the legends should say so...
Retrieved from "https://edutechwiki.unige.ch/mediawiki/index.php?title=OpenScad_beginners_tutorial&oldid=74992"