Topo-kit
| Auteur-e-s | Utilisateur:Romain Dewaele |
|---|---|
| Année de fabrication | 2016 |
| Technologie utilisée | Découpe laser |
| Type | Activité, Kits constructif |
| Domaine d’enseignement | Géographie |
| Niveau d’enseignement | Ecole primaire (moyen) |
| Public cible | Enfants |
| Public cible (Age) | 10-11 ans |
| Mots clés | cartes topographiques |
| Lien vers le cours STIC | https://edutechwiki.unige.ch/fr/STIC:STIC III (2016) |
| Fichier source | Fichier:Topo-kit.zip |
Les cartes topographiques sont des projections d'un espace 3D (et même sphérique à l'échelle de la planète) sur une surface en 2 dimensions. La lecture d'une carte n'est donc pas toujours intuitive et nécessite un apprentissage, en particulier pour la représentation de la dimension verticale, le relief. Le relief est principalement représenté sur les cartes topographiques à l'aide des courbes de niveau et des points d'altitude. Les courbes de niveaux sont formées par l'ensemble des points du reliefs situés à une même altitude.
Ce kit s'adresse aux apprentis randonneurs, aux scouts, ou à toute personne ou groupe désirant apprendre à lire le relief d'une carte. C'est un sujet qui est également abordé à l'école primaire: plan d'étude romand. Voici un exemple de cours et d'exercice donné en 7P à Nyon.
Le kit peut être utilisé lors d'activités pédagogiques dont les objectifs sont:
Comprendre la notion d'altitude Comprendre la notion de courbes de niveau Comprendre la notion d'équidistance La pente du relief est proportionnelle au rapprochement des courbes de niveau Le chemin le plus facile n'est pas forcement le plus court en distance horizontale Comprendre la notion de kilomètre effort Savoir calculer la distance en kilomètre effort d'un parcours
Un premier fichier a été créé dans illustrator. C'est celui qui a été utilisé pour la carte. Ensuite, la carte a été dupliquée 3 fois afin de préparer le fichier pour la découpe. En effet, pour économiser du bois, il n'est pas nécessaire d'imprimer toutes les pièces séparément: il est possible d'en imbriquer certaines (une sur 2 ici) car les trous seront recouverts par d'autre étages.
Les couleurs ont été changées pour correspondre aux couleurs utilisées par trotec job control, dans lequel un profil personnalisé a été créé:
- pour la forêt: noir #000000 -> gravure à 40
- pour l'intérieur de la rivière: rouge #ff0000 -> gravure à 60
- pour les rives de la rivière: bleu #0000ff -> gravure à 80
- pour les chemins et habitations: bleu #336699 -> gravure à 100
- pour les courbes de niveau: cyan #00ffff -> découpe à 100
Le kit a été découpé dans du bouleau de 4mm d'épaisseur

Un relief 3D a également été créé en utilisant un script qui permet de créer des courbes de niveaux à partir d'une "height map" en noir et blanc. De tels "puzzles" à coller pourraient également être utilisés en classe, et facilite beaucoup la création des fichiers nécessaires. Voir la page Modèles 3D tranchés pour la découpe laser.
Un premier fichier a été créé dans illustrator: lien vers le fichier. C'est celui qui a été utilisé pour la carte. Ensuite, la carte a été dupliquée 3 fois afin de préparer le fichier pour la découpe. En effet, pour économiser du bois, il n'est pas nécessaire d'imprimer toutes les pièces séparément: il est possible d'en imbriquer certaines (une sur 2 ici) car les trous seront recouverts par d'autre étages. Les couleurs ont été changées pour correspondre aux couleurs utilisées par trotec job control, dans lequel un profil personnalisé a été créé:
- pour la forêt: noir #000000 -> gravure à 40
- pour l'intérieur de la rivière: rouge #ff0000 -> gravure à 60
- pour les rives de la rivière: bleu #0000ff -> gravure à 80
- pour les chemins et habitations: bleu #336699 -> gravure à 100
- pour les courbes de niveau: cyan #00ffff -> découpe à 100
Le kit a été découpé dans du bouleau de 4mm d'épaisseur
Une activité de groupe en deux parties a été développée.
Dans une première partie, le groupe doit construire le modèle 3D tranché en s'aidant de la carte à la même échelle, et répondre à une série de questions favorisant le mapping mental entre l'espace 3D et le plan 2D.
Dans la deuxième partie, le groupe reçoit une autre carte, mais cette fois sans modèle 3D et devra répondre à des questions similaires. Cela permet de consolider les apprentissages de l'apprenant, et pour l'enseignant de les évaluer.
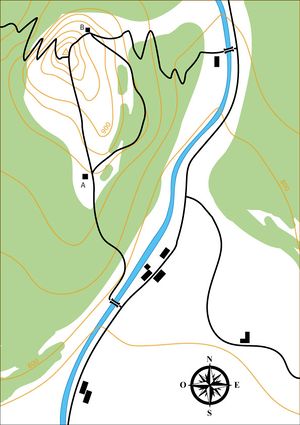
On voit ici le kit monté avec les différentes courbes de niveaux empilées les unes au dessus des autres, ainsi que la carte qui représente ce relief. Le relief contient une montagne et une vallée au fond de laquelle coule une rivière.
Voici la liste des questions à répondre lors de la première activité, classées par ordre de difficulté:
- Quelle est l'altitude du chalet A?
- Quelle est l'altitude du chalet B?
- Dans quel sens coule la rivière?
- En se basant sur la carte, quel semble être le chemin horizontal le plus court (sans tenir compte du relief) pour aller du chalet B au chalet A?
- En prenant en compte le relief cette fois, quel est le chemin le moins fatiguant pour aller du chalet B au chalet A?
- Depuis le sommet de la montagne, quelle est la direction la plus pentue?
- Et la moins en pente?
- Au total, de combien de mètres monte-t-on pour aller du pont sud au sommet de la montagne?
- Et du sommet de la montagne au pont nord?
- Quelle est l'équidistance sur cette carte?
- Comme un kilomètre à plat n'est pas aussi difficile qu'un kilomètre en montée, on calcule souvent les distances en "kilomètres effort". Pour cela, il suffit d'ajouter aux kilomètres horizontaux du trajet: 1km pour chaque 100m de montée, et 1km pour chaque 300 de descente. En sachant cela, combien de kilomètres effort parcourt-on lors d'une balade qui part du pont sud, passe par le chalet A, le sommet de la montagne, le chalet B, le pont nord, et enfin retour au pont sud, si la boucle fait 10km à plat?
- Trace le profil d'altitude approximatif du chemin reliant le chalet A au chalet B passant par le sommet de la montagne.
Solutions:
- entre 840 et 860m, mais très proche de 860
- entre 900 et 920m
- du nord vers le sud
- le chemin le plus droit semble être le plus court sans tenir compte du relief
- en prenant le relief en compte, on s'aperçoit qu'il passe en fait pas le sommet de la montagne pour ensuite redescendre au chalet A, alors que l'autre chemin descend doucement en pente douce. C'est donc le chemin qui passe par l'est qui est le plus court
- la face nord-ouest est la plus pentue
- le sud est la direction la moins en pente
- entre 160 et 180 mètres de dénivelé positif
- entre 140 et 160 mètres de dénivelé négatif
- 20m
- 10km + 170/100 + 150/300 = 12.2km
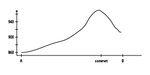
Cette activité peut bien sûr être adaptée en fonction du niveau des apprenants, et des questions peuvent facilement être ajoutées ou enlevées.
Dans la deuxième partie, les apprenants ne pourront utiliser qu'une carte pour répondre aux questions. Il pourra s'agir d'une carte similaire à celle inventée ici, ou d'une vraie carte. L'activité pourrait consister comme ici à répondre à des questions ou, si le niveau le permet, à planifier une randonnée.
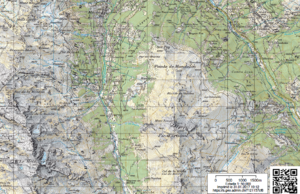
Exemple de questions sur une vraie carte:
- Quel est le point le plus haut sur cette carte?
- Quel est le point le plus bas sur cette carte? (indication, les rivières coulent en général vers l'océan...)
- Quelle est l'équidistance sur cette carte?
- Pour aller de "Pralong" (1608m) à "Mejonèche" (1055m), deux itinéraires s'offrent à nous: passer par Noveli, le col de Méribé, puis la Meina, ou passer par Mâche, la Crêta, puis la Luette. D'après vous quel est le chemin le plus court en kilomètres horizontaux? Quel est le chemin le plus rapide à pied?
- À quelle altitude se trouve le lac entre le Mont Loéré et le Mont Cauille?
Réponses:
- 3213m
- ~870m
- 20m
- À première vue, le chemin passant par le col à l'air le plus court. Mais en réalité il nous fait partir de 1605 pour monter jusqu'à 2702m d'altitude, et enfin redescendre à 1055m, ce qui rajouterait (2702-1605)/100 + (2702-1055)/300 = 11.97 + 5.49 = 17.46 kilomètres efforts au parcours. En revanche, l'autre itinéraire descend lentement jusqu'à 997m pour remonter légèrement à la fin jusqu'à 1055m, ce qui n'ajoute que (1605-997)/300 + (1055-997) = 2.03 + 0.58 = 2.61 kilomètre efforts. Le deuxième itinéraire semble donc être le plus rapide.
- ~2370m