« STIC:STIC III (2018)/Brodeuse phi » : différence entre les versions
| Ligne 32 : | Ligne 32 : | ||
La première partie a consisté à effectuer une représentation par une image vectorielle (svg) de la future broderie. | La première partie a consisté à effectuer une représentation par une image vectorielle (svg) de la future broderie. | ||
[[Fichier:Spirale d'or inkscape.png|alt=la spirale d'or modélisée avec inkscape.|vignette|la spirale d'or modélisée avec inkscape.]] | |||
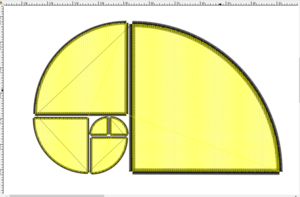
[[Fichier:Spirale d'or avec inkstitch.png|alt=La spirale d'or avec inkstitch|vignette|La spirale d'or avec inkstitch]] | |||
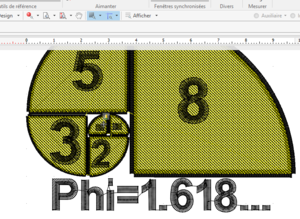
[[Fichier:Spirale d'or avec stitch era.png|alt=La spirale d'or avec stitch era|vignette|La spirale d'or avec stitch era]] | |||
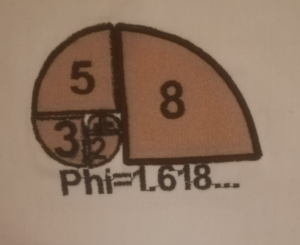
[[Fichier:La spirale d'or brodée.png|alt=La spirale d'or brodée|vignette|La spirale d'or brodée]] | |||
<gallery> | <gallery> | ||
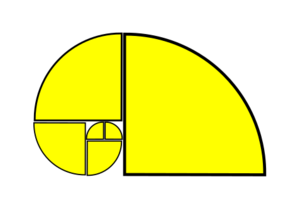
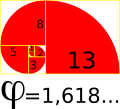
Fichier:Phi.svg|alt=La spirale d'or|La spirale d'or | Fichier:Phi.svg|alt=La spirale d'or|La spirale d'or | ||
</gallery> | </gallery> | ||
Version du 14 décembre 2018 à 00:43
Physicalisation du nombre d'or par la brodeuse
Description
Considéré comme la proportion parfaite en architecture ou en art, le nombre d'or se retrouve aussi dans dans certain phénomène naturel comme la répartition des étamines sur la fleur de tournesol.
Le nombre d'or φ se définit comme l'unique solution positive de l'équation x^2-x-1=0.
Suite de Fibonnaci
La suite de Fibonacci est une suite d'entiers où chaque terme est égale à la somme des deux termes précédents, les deux premiers termes étant égaux à 1.
Fn={1,1,2,3,5,...}
Si F(n) désigne le nième terme de la suite de Fibonacci et F(n-1) le n-1 ème terme de la suite, alors le rapport F(n)/F(n-1) lorsque n tend vers l'infini est égal à φ.
Géométrie et Spirale d'or
Du point de vue géométrique, soit deux longueur a et b (non-nulles) dont le rapport de a sur b est égal au rapport de a + b sur a. Le nombre d'or φ est alors la proportion a/b.
Les longueurs a et b représente un rectangle considéré parfait en art ou en architecture. Il est possible de construire une série de rectangle d'or par une spirale logarithmique particulière.
On trace un demi-cercle de rayon r. Puis d'une extrémité de l'arc de cercle, on continue à tracer un quart de cercle de rayon 2r. Puis à l'extrémité de l'arc de cercle, on trace un quart de cercle de rayon 3r,...., à la nième extrémité d'arc de cercle, on trace un quart de cercle de rayon égale à la somme des rayon des deux quarts de cercle précédents.
On retrouve ainsi la suite de Fibonacci où le rayon r(n)=r(n-1)+r(n-2).
Dès lors le rapport r(n)/r(n-1) tend vers φ pour n grand et les côtés r(n) et r(n-1) forment un rectangle d'or.
Objectif
Beaucoup de propriétés mathématiques ont été découvertes par la géométrie avant le développement des ordinateurs. La construction d'une spirale d'or est une solution élégante pour approcher le nombre φ qui est irrationnel.
La brodeuse devient ainsi un outil optimal pour représenter physiquement le nombre d'or via la spirale et les rectangles d'or.
Représentation physique
La première partie a consisté à effectuer une représentation par une image vectorielle (svg) de la future broderie.