Pensée computationnelle

De EduTech Wiki
Aller à la navigation Aller à la recherche

Cet article est en construction: un auteur est en train de le modifier.

En principe, le ou les auteurs en question devraient bientôt présenter une meilleure version.

Introduction

La pensée computationnelle (Computational Thinking en anglais, abrégé CT dans le reste de l’article) est un terme se référant, de manière plutôt flexible, à un ensemble d'habilités, compétences et procédures qui facilitent la résolution de problèmes en s'appuyant sur des principes tirés des sciences informatiques (Computer Science).

Bien que des concepts similaires au CT aient déjà été introduits dans les années 1960 (Guzdial, 2008; Tedre & Denning, 2016) et réactualisés une première fois dans les années 1980, notamment en relation avec le langage LOGO de Papert (1980) utilisé pour apprendre aux enfants la programmation, le terme a connu une plus grande célébrité à partir de 2006, suite à l'article "Computational thinking" de Jeannette M. Wing (Wing, 2006). Dans cet article, Wing suggère que la pensée computationnelle doit être une compétence fondamentale - i.e, "fundemantal skill" dans le texte (Wing, 2006 p. 33) - pour tout le monde, pas simplement pour les informaticiens : « [t]o reading, writing, and arithmetic, we should add computational thinking to every child's analytical ability » (Wing, 2006, p. 33).

Le CT est à la base de plusieurs mouvements qui essaient de (ré)définir le rôle de l'informatique dans l'éducation, surtout aux USA (Grover & Pea, 2013), comme par exemple le mouvement Computer Science for All ou Hour of code. Des ressources sur le CT et la manière de l'enseigner à l'école sont mises à disposition sur internet par plusieurs sources, de Google à la BBC. Le concept de CT n'est cependant pas sans critique à la fois au niveau théorique et pratique. Sur le plan théorique, le CT a été critiqué en relation au manque d'une définition claire et, surtout, à la promotion d'atteintes exagérées sur les bénéfices en termes de généralisation à d’autres domaines (Grover & Pea, 2013; Tedre & Denning, 2016). Sur le plan pratique, c'est-à-dire au niveau de l'enseignement dans les écoles, le débat concerne l'utilité et/ou la nécessité de considérer le CT une matière fondamentale, et si cette matière doit être enseignée en ajoute, en substitution, ou en intégration avec d'autres matières fondamentales (RTS, 2016).

Définitions et composantes du Computational Thinking

Selon la première définition du CT propose par Wing (2006, p. 33), « computational thinking involves solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science ». Cette definition a été ensuite mise à jour par Wing elle-même en 2011 : « [c]omputational thinking is the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information-processing agent » (Wing, 2011). Sur la base de ces définitions, Aho (2012) propose une version simplifiée :

We consider computational thinking to be the thought processes involved in formulating problems so their solutions can be represented as computational steps and algorithms (Aho 2012, p. 832)

Aho (2012) suggère également que la définition du CT doit forcément tenir compte à priori de la définition de computation. Si cette définition peut être établie grâce à des modèles existants en informatique (Sipser, 2012), sur le plan pragmatique la computation dépend intrinsèquement de l’agent qui l’effectue, que ce soit une machine ou un être humain. Wing propose une définition très large du concept de computation « [b]y ‘computing’ I mean very broadly the field encompassing computer science, computer engineering, communications, information science and information technology » (Wing, 2008, p. 3717, note de pied de page).

Au contraire, déjà à partir des années ’80, Denning et al. (1989) identifient dans le « computing » une discipline définie de la manière suivante : « The discipline of computing is the systematic study of algorithmic processes that describe and transform information: their theory, analysis, design, efficiency, implementation, and application. The fundamental question underlying all of computing is, “What can be (efficiently) automated? » (Denning et al., 1989, p. 12; voir également Denning & Martell, 2015 pour une description plus approfondie des principes fondamentaux du computing).

En fonction de cette définition, Denning (2016) souligne qu’un algorithme n’est pas une séquence d’étapes quelconque mais doit présupposer la présence d’un modèle :

An algorithm is not any sequence of steps, but a series of steps that control some abstract machine or computational model without requiring human judgment. Computational thinking includes designing the model, not just the steps to control it. (Denning, 2016, p. 33).

Malgré la difficulté à cerner une définition précise de CT, il existe un certain accord sur les éléments qui composent la pensée computationnelle.

Les éléments de la pensée computationnelle

Les 4 composantes "principales" de la pensée computationnelle.

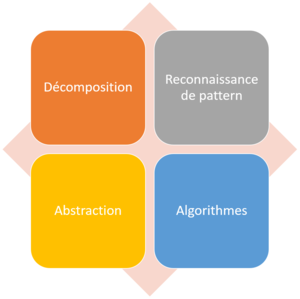
Le nombre d’éléments qui compose le CT peuvent varier en nombre et complexité des concepts. Par exemple, dans une version simplifiée, le guide proposé par la BBC identifie quatre éléments principaux :

  1. Décomposition
    L’action de diviser un problème complexe ou un système en petites parties plus simples à gérer ;
  2. Reconnaissance de pattern
    L’action d’identifier des similarités entre problèmes ou à l’intérieur du même problème donné ;
  3. Abstraction
    L’action de se focaliser exclusivement sur les parties importantes du problème ;
  4. Algorithmes
    L’action de trouver une solution à travers une règle composée par une série d’étapes.

De manière plus formelle, Aho (2012, pp. 39–40) propose une synthèse des éléments sur lequel il existe un certain accord :

  • Abstraction et généralisation de pattern (y compris modèles et simulations)
  • Traitement systématique de l’information
  • Utilisation de systèmes et représentations symboliques
  • Notions algorithmiques de contrôle du flux
  • Décomposition structurelle d’un problème (modularisation)
  • Pensée itérative, récursive et parallèle
  • Logique conditionnelle
  • Contraintes d’efficacité et de performance
  • Débogage et contrôle systématique des erreurs

Des concepts similaires sont proposés par les ressources éducatives de Google sur le CT :

  • Abstraction : identifier et extraire les informations saillantes pour définir les idées principales ;
  • Design d’algorithmes : créer une série ordonnée d’instructions pour résoudre des problèmes similaires ou exécuter des tâches ;
  • Automation : exploiter ordinateurs ou machines pour exécuter des tâches répétitives ;
  • Analyse de données : extraire du sens depuis des données en identifiant des patterns ;
  • Recueille de données : collecter des données ;
  • Représentation de données : illustrer et organiser les données avec des graphiques, mots, images appropriées ;
  • Décomposition : diviser les données, les processus de traitement, ou les problèmes en partie plus petites et simples à gérer ;
  • Parallélisation : traitement simultané de petits sous-tâches pour atteindre efficacement un objectif commun ;
  • Généralisation de patterns : créer des modèles, règles, principes ou théories tirés de l’observation de pattern afin de tester la prédiction de résultats ;
  • Pattern recognition : observer des patterns, trends et régularités dans les données ;
  • Simulation : développer des modèles pour imiter des processus dans le monde réel.

Le rôle fondamental de l’abstraction pour la création d’algorithmes

Parmi les éléments qui composent le CT, Wing (2008, p. 3718) identifie l’abstraction en tant qu’élément fondamental : « [t]he abstraction process—deciding what details we need to highlight and what details we can ignore—underlies computational thinking ». Malgré le fait que dans l’imaginaire collectif le terme abstrait soit associé souvent à quelque chose de difficile ou indéfini, en informatique – et par conséquent en CT – l’abstraction est plutôt l’inverse : la simplification d’un processus à l’essentiel. L’abstraction peut être utilisée à plusieurs niveaux, que ce soit d’un point de vue théorique ou technique. Sur le plan technique, le langage de programmation ou les outils auteurs permettent de faire abstraction par rapport à des niveaux plus bas du dispositif (e.g. afficher un message à l’écran, imprimer, etc.). Sur le plan théorique, l’abstraction est essentielle dans l’identification et généralisation de pattern, surtout lorsqu’on a à faire avec une grande quantité de données. De plus, selon Wing (2008), l’abstraction dans le traitement de l’information est également l’élément qui permet de différencier le CT d’autres formes de pensée (voir plus bas dans la section critiques du CT).

L’abstraction sert principalement pour identifier le meilleur algorithme pour résoudre le problème donné ou exécuter la tâche déterminée. D’après Wing (2008, p. 3718) « [a]n algorithm is an abstraction of a step-by-step procedure for taking input and producing some desired output ». Si on compare cette définition avec une définition "scolastique" – par exemple, « an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output » (Cormen, Leiserson, Rivest, & Stein, 2009, p. 5) – on rélève comment l’accent est effectivement mis sur l’abstraction. Importance confirmée d’ailleurs dans le challenge identifié par Wing (2011) :

« Computer scientists already know the value of thinking abstractly, thinking at multiple levels of abstraction, abstracting to manage complexity, abstracting to scale up, etc. Our immediate task ahead is to better explain to non-computer scientists what we mean by computational thinking and the benefits of being able to think computationally. Please join me in helping to spread the word! ».

Critiques du CT

Le concept de CT fait l’objet de plusieurs types de critiques, que ce soit au niveau théorique ou pratique. Nous proposons par la suite une liste de points critiques qui ont été soulevés dans la littérature, surtout dans un article de Tedre et Denning (2016), mais également quelques considérations plus générales.

Manque d’une définition précise et atteintes disproportionnées

La première critique qui est souvent portée au concept de CT concerne le manque d’une définition précise et partagée. Bien qu’il s’agisse d’une critique commune à tout concept théorique, dans le cas du CT il existe des circonstances particulières qui augmentent la problématique. Ces circonstances concernent le contexte fondamental que le CT essaie d’occuper en tant que compétence de base universelle. Tedre et Denning (op. cit.) affirment cependant que l’attribution au CT d’objectifs inatteignables crée des atteintes disproportionnées, surtout en relation avec la possibilité de généraliser les connaissances/compétences du CT à d’autres domaines. Les auteurs suggèrent d’appliquer une perspective historique au CT pour éviter de proposer cycliquement les mêmes concepts et, surtout, répéter les mêmes erreurs. Une erreur fréquente identifiée par Tedre et Denning consiste à affirmer que les compétences acquises grâce au CT puissent être automatiquement généralisées à d’autres domaines. Cette affirmation, selon les auteurs, a déjà été infirmée dans les années ’80 (Pea & Kurland, 1984), et également par des recherches plus récentes menées par Guzdial (2015).

Tous les problèmes ne sont pas computationnels

Une autre critique qui a été soulevée au sujet du CT concerne le fait que tous les problèmes ne possèdent pas forcément une solution computationnelle. Par exemple Jones (2011) souligne comme :

« There are a number of problems that would seem to lie outside the realm of computational thinking – for example, when I consider how to revise a draft of a story. While I go through a problem-solving process in thinking about the changes I wish to make, there are a number of elements that I consider which seem very different from a computational process, such as questions of aesthetics, or what I personally wish to gain from the story itself, as well as what I wish my reader to gain from it. » (Jones, 2011)

Jones (ibid.) fait également l’exemple des problèmes moraux ou éthiques qui ne peuvent pas être résolus sans faire recours à des considérations sur les valeurs et les idées personnelles ou qui appartiennent à un cadre social de référence. Ces problèmes, souvent, n’ont pas une solution claire et nette. Cette critique se réfère probablement à la visée généralisée des bénéfices du CT, car la « naissance » elle-même de la computation automatisée, avec les travaux de Turing (1936), est basée sur l’impossibilité de mener à bien certaines types de computation. L’une des branches de la théorie de la computation (Sipser, 2012) s’intéresse d’ailleurs à déterminer quels sont les problèmes pour lesquelles on peut calculer une solution et ceux qui sont, au contraire, impossible à traiter.

Sur le versant opposé on retrouve les travaux de Marvin Minsky (1985, 2006), en relation avec l’intelligence artificielle, selon lesquels la pensée des êtres humains est fondamentalement de type computationnel. Si on arrive à voir les émotions, les intuitions, les préférences, ou plus en général tout ce qui n’est pas considéré strictement rationnel simplement comme « d’autres formes de pensée », on peut s’apercevoir que notre pensée suit une progression des formes plus simples au plus complexes, ressemblant ainsi à des algorithmes. En d’autres termes, si on arrive à faire abstraction de certaines particularités de la pensée humaine, on peut la considérer computationnelle et, par extension, toute résolution de problèmes faites par l’esprit humain est forcément computationnelle.

Le CT n’est pas une forme de pensée distincte

Une dernière critique que nous proposons dans cet article concerne la distinction entre le CT et d’autres formes de pensée, notamment en relation avec la résolution de problèmes (Newell & Simon, 1972). La psychologie cognitive s’occupe depuis des nombreuses années des stratégies et processus qui sont mobilisé, à différent niveaux et selon différent degrés d’expertise, pour résoudre des problèmes. En quoi, donc, le CT serait-il une forme de pensée distincte par rapport à d’autres types de résolution de problèmes ?

La réponse à cette question dépend étroitement du champ d’application du CT et les moyens déployées pour l’enseigner/exploiter. Par exemple, il existe des nombreuses ressources qui visent l’enseignement de la pensée computationnelle sans utiliser des dispositifs numériques, s’appuyant plutôt sur des activités comme des jeux ou des puzzles. Dans ce sens, il est peut-être difficile de pouvoir identifier nettement une différence avec d’autre formes de pensée.

Une clé de lecture possible pour différencier la pensée computationnelle d’autres formes de pensée réside donc plutôt dans le siège de la computation et dans la nécessité de transfert de la « solution ». En effet, si on considère le CT plus spécifiquement dans le cadre de la programmation et de la computation, l’objectif n’est pas de résoudre directement un problème, mais de formuler le traitement de l’information afin qu’une machine puisse le faire à notre place. Dans cette perspective, la particularité du CT n’est pas liée à une différence par rapport à d’autres formes de pensée de type logico-mathématique, mais plutôt à des contraintes qui sont déterminée par le passage d’un système computationnel (le cerveau) à un autre système computationnel (l’ordinateur). Les deux "agents computationnels", malgré un certain recouvrement de termes surtout dans l’intelligence artificielle (e.g. neural network), diffèrent sensiblement dans leur fonctionnement. Du Boulay et al. (1981) parlent à ce propos de notional machine, c’est-à-dire une représentation mentale de ce que la machine peut ou ne peut pas faire (Guzdial, 2015).

Les grands principes du computing

On peut faire un parallèle entre la difficulté à cerner le concept de CT avec la difficulté que l'informatique a eu à trouver sa propre place en tant que science détachée des mathématiques et de la logique d'une part, et de ingénierie de l'autre. Denning & Martell (2015, p.12) propose 6 grands principes à la base du computing :

  1. Communication
    Transférer de l'information d'un endroit à l'autre de manière fiable.
  2. Computation
    Déterminer ce qui peut être automatisé/calculé/computé de manière efficace et ce qui ne peut pas.
  3. Récollection
    Représentation, stockage, récupération, ... de l'information, comme par exemple dans les bases de données
  4. Coordination
    Utilisation de plusieurs dispositifs/agents computationnels en même temps.
  5. Évaluation
    Mesurer à quel point les systèmes arrivent à mener à bien les opérations attendues, y compris l'application de la méthode expérimentale pour comparer des technologies.
  6. Design
    Structuration et architecture de systèmes complexes.

Les auteurs suggèrent que tous les domaines qui font partie des sciences informatiques se réfèrent à un principe ou, plus souvent, plusieurs principes à la fois. Par exemple, on peut voir internet comme :

  • Un système de communication (principe 1), comme par exemple à travers le protocole HTTP pour le Web.
  • Un système de récollection de données (principe 3), comme dans le cadre des moteurs de recherche.
  • Un système de coordination entre plusieurs agents (principe 4), notamment à travers les échanges client/serveur, les serveurs DNS qui transforment les noms de domaines en addresses IP, etc.

Une des conséquences de l'adoption des grands principes concerne la variabilité de connaissances nécessaires pour chaque principe (ou la combinaison entre principes). Par exemple, les connaissances nécessaires à un développeur web ne sont pas les mêmes nécessaires à un ingénieur système, tandis que souvent, dans l'imaginaire collectif, la figure de l'informaticien englobe toute connaissance confondue.

Par dérivation, la pensée computationnelle n'est pas appliquée de manière homogène en informatique et doit forcement s'adapter aux contextes, objectifs et limitations de chaque principe. Néanmoins, il existe un trait d'union dans les différentes sous-domains : le traitement de l'information.

Le rôle fondamentale de l'information

Les six grands principes fondamentaux permettent de créer des traits d'union entre le computing et d'autres domaines scientifiques à travers le rapport avec l'information. Aucun autre domaine scientifique s'est occupé de manière aussi abstraite de l'information en tant que telle : dans les autres domaines l'information consiste toujours dans quelque chose de plus ou moins concret (des mots, des séquences d'ADN, des processus cognitifs, ...). Denning & Martell (ibid.) identifient deux raisons qui différencient le computing des autres sciences (p. 15, adapté) :

  1. « First, computing emphasizes the transformation of information, not simply its discovery, classification, storage, and communication. Algorithms not only read information structures, they modify them. [...] »
  2. « Second, the structures of computing are not just descriptive, they are generative. An algorithm is not just a description of a method for solving a problem, it causes a machine to solve the problem. »

Ces deux caractéristiques renvoient au concept de notional machine introduit plus haut dans l'article. En effet, la transformation de l'information et la résolution de problèmes à travers une machine nécessitent d'une idée précise de ce qu'une machine peut ou ne peut pas faire.

Computing Education

Sur la base de ce principe, Guzdial (2015) propose le concept de computing education pour articuler des concepts qui sont souvent utilisés comme synonymes, mais qui en réalité ne le sont pas : programmation, informatique (computer science), et computing. Le schéma à droite explique de manière graphique les relations suivantes :

  • La programmation est l'une des composantes de l'informatique, mais pas la seule. La programmation est "the process of writing programs. Programs do not have to be text. A variety of notations can instruct a computer to behave in a certain way. That behavior is a process. A program specifies a computational process which can be executed some time in the future" (Guzdial, 2015, p. 2)
  • L'informatique est la science qui s'occupe du coeur de la computation d'un point de vue technique et théorique (Sipser, 2012)
  • Le computing, enfin, selon la définition proposé par Denning et al. (1989), est la science qui s'occupe du traitement automatisé de l'information. Par conséquent, le computing dépasse les bornes de l'informatique et joue le rôle de trait d'union avec d'autres disciplines comme les sciences de la communication et de l'information, le développement au niveau hardware et software, mais également toute les disciplines scientifiques qui peuvent bénéficier de la computation, par exemple dans la modélisation ou simulation de phénomènes (e.g. biologie, psychologie cognitive, etc.)

En fonction de cette hiérarchie, Guzdial (2015) fait l'hypothèse que la programmation reste la meilleure manière pour développer une compréhension du computing et tout ce qui est connecté avec ce principe, notamment tout ce qui relève du domaine du numérique. Cependant, la programmation n'est pas la seule fonction des dispositifs numériques et, encore moins, du computing. La plupart des personnes qui utilisent un ordinateur ne vont jamais écrire une seule ligne de code, mais vont se limiter à instruire la machine à travers des interfaces graphiques qui permettent d'exécuter certaines opérations. Ces opérations, de plus, ne concernent souvent pas directement des calcules, mais plutôt de la communication à travers du texte (écrit et audio), et des représentations graphiques (images et vidéo). Cette capacité d'utiliser le numérique pour atteindre des objectifs en dehors du domaine auto-référentiel du computing est souvent identifiée sous le terme de digital literacy.

Un autre aspect à approfondir concernant la pensée computationnelle concerne ainsi son articulation avec les Technologies de l'Information et de la Communication (TIC), et en particulier, dans la perspective éducative, dans leur dérivation pour l'Enseignement (TICE).

Conclusion

Bibliographie

  • Aho, A. V. (2012). Computation and computational thinking. Computer Journal, 55, 833–835.
  • Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Alogrithms (3rd ed.). Cambridge, MA: MIT press.
  • Denning, P. J. (2016). Remaining Trouble Spots With Computational Thinking. Cacm, 60, 33–39.
  • Denning, P. J., Comer, D. E., Gries, D., Mulder, M. C., Tucker, A., Turner, A. J., & Young, P. R. (1989). Computing as a discipline. Computer, 22, 63.
  • Denning, P. J., & Martell, C. H. (2015). Great Principles of Computing. Cambridge, MA: MIT press.
  • Du Boulay, B., O’Shea, T., & Monk, J. (1981). Black box inside the glass box: Presenting computing concepts to novices. Int. J. Man-Machine Studies, 14, 237–249.
  • Grover, S., & Pea, R. (2013). Computational Thinking in K-12: A Review of the State of the Field. Educational Researcher, 42, 38–43.
  • Guzdial, M. (2008). Paving the way for computational thinking. Communications of the ACM, 51, 25.
  • Guzdial, M. (2015). Learner-Centered Design of Computing Education. Research on Computing for Everyone. Morgan & Claypool.
  • Jones, E. (2011). The Trouble with Computational Thinking. In ACM. Retrieved from https://c.ymcdn.com/sites/www.csteachers.org/resource/resmgr/JonesCTOnePager.pdf
  • Minsky, M. (1985). The Society of Mind. New York, NY: Simon & Schuster.
  • Minsky, M. (2006). The Emotion Machine. Commonsense Thinking, Artificial Intelligence, and the Future of the Human * Mind. New York, NY: Simon & Schuster.
  • Newell, A., & Simon, H. A. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice-Hall.
  • Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.
  • Pea, R. D., & Kurland, D. M. (1984). On the Cognitive Effects of Learning Computer Programming. New Ideas Psychology, 2, 137–168.
  • RTS. (2016). Faut-il obliger les enfants à suivre des cours de programmation informatique à l’école? Suisse. Retrieved from https://www.rts.ch/play/radio/forum/audio/faut-il-obliger-les-enfants-a-suivre-des-cours-de-programmation-informatique-a-lecole?id=7638246&station=a9e7621504c6959e35c3ecbe7f6bed0446cdf8da
  • Sipser, M. (2012). Introduction to the Theory of Computation (3rd ed.). Cengage Learning.
  • Tedre, M., & Denning, P. J. (2016). The Long Quest for Computational Thinking. In Koli Calling Conference on Computing Education Research (pp. 120–129).
  • Turing, A. M. (1936). On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society, 230–265.
  • Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49, 33–35.
  • Wing, J. M. (2008). Computational thinking and thinking about computing. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 366, 3717–25.
  • Wing, J. M. (2011). Research Notebook: Computational Thinking-What and Why? Retrieved from http://www.cs.cmu.edu/link/research-notebook-computational-thinking-what-and-why

Ressources

Récupérée de « https://edutechwiki.unige.ch/fmediawiki/index.php?title=Pensée_computationnelle&oldid=95898 »