STIC:STIC IV (2015)/Cubricks
Cet article est en construction: un auteur est en train de le modifier.
En principe, le ou les auteurs en question devraient bientôt présenter une meilleure version.
Introduction
Description
| Je souhaite réaliser un cube à assembler à la manière d'un tetris en 3D.
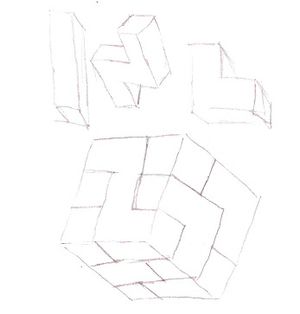
Le but est d'aider par la manipulation des différentes pièces à entrainer la rotation mentale et la compréhension de la géométrie en sollicitant des emboîtages selon des angles, des arêtes, et des surfaces définies, lors d'un cours de géométrie pour les petits. Chaque unité cubique créée peut devenir la base de construction d'unités plus grandes (comme un maçon, l'enfant fabrique ses briques (cubes) pour construire ensuite un ouvrage plus grand). On peut voir sur le croquis ci-joint à quoi cela ressemblerait, en tenant compte que cette ébauche qui comporte certaines erreurs. |
Public cible
Le Cubricks s'adresse à des enfants de classe de 5p à 8p, de 9 à 12 ans. Selon le Plan d'Etude Romand (PER) cet objet pourrait s'inscrire dans une activité plutôt ludique en lien avec les cours de Mathématiques et Sciences de la nature, notion de repérage dans l'Espace du Cycle 2:
MSN 21 — Poser et résoudre des problèmes pour structurer le plan et l'espace…
- …en imaginant et en utilisant divers outils de représentation
- …en menant des observations répétées
- …en se référant à diverses sources
- …en triant et organisant des données
- …en confrontant et en communiquant ses observations, ses résultats, ses constats, ses interprétations
- …en mobilisant, selon la situation, la mesure et/ou des outils mathématiques
- …en se posant des questions et en exprimant ses conceptions
Progression des apprentissages: Éléments pour la résolution de problèmes
Résolution de problèmes géométriques en lien avec le repérage, ainsi que les figures et les transformations étudiées:
- tri et organisation des informations (liste, tableau, schéma, croquis,…)
- mise en œuvre d'une démarche de résolution
- ajustement d'essais successifs
- pose d'une conjecture, puis validation ou réfutation
- déduction d'une ou plusieurs informations nouvelles à partir de celles qui sont connues
- vérification, puis communication d'une démarche et d'un résultat en utilisant un vocabulaire ainsi que des symboles adéquats
Attentes fondamentales: résout des problèmes géométriques en faisant appel à une ou plusieurs des composantes suivantes :
- choix et mise en relation des données nécessaires à la résolution
- mobilisation de propriétés de figures et de transformations
- utilisation d'un système de repérage pour situer des objets dans le plan
- utilisation d'outils de construction appropriés
- vérification de la pertinence du résultat
- communication de la démarche et du résultat en utilisant un vocabulaire adéquat