« Clustering et classification hiérarchique en text mining » : différence entre les versions
| Ligne 63 : | Ligne 63 : | ||
====Complete linkage==== | ====Complete linkage==== | ||
===Regroupement basés sur la distance === | |||
====k-mean==== | |||
====k-medoid==== | |||
===Autres méthodes=== | |||
'''Méthodes hybrides : Eclater et regrouper (Scatter-Gather)''' | |||
D'autres méthodes existent dont la mise en oeuvre peut être plus complexe comme | |||
* le '''Buckshot''' qui cherche à améliorer les algorithmes de type ''k-means'' en sélectionnant <math>\sqrt{k\cdot n}</math> graines au lieu de <math>k</math> puis les fusionnent en k graines ; | |||
* la '''Fractionalisation''' qui répartit le corpus en sous-corpus de tailles réduites, réalise une agglomération des corpus pour en réduire le nombre puis classifie le corpus réduit. | |||
'''Méthodes basées sur la fréquence des termes''' | |||
D'autres méthodes existent encore, basées entre autres sur la fréquence de présence des termes dans les documents. | |||
Pour de plus amples informations sur ces méthodes, voir [http://www.charuaggarwal.net/text-cluster.pdf] | |||
== Références == | == Références == | ||
Version du 30 octobre 2014 à 18:06
Cet article est une ébauche à compléter. Une ébauche est une entrée ayant un contenu (très) maigre et qui a donc besoin d'un auteur.
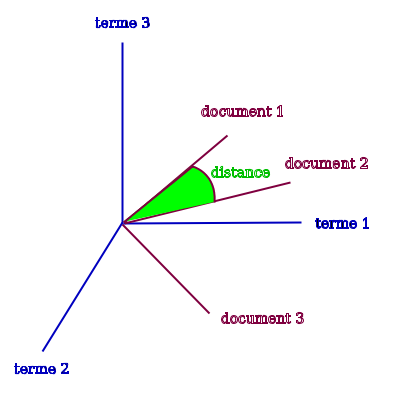
clustering basé sur une distance
Définition d'une distance
Voir la page Text mining pour un survol.
Distance du cosinus
La distance la plus couramment utilisée est la distance du cosinus ou cosine qui est définie comme
où dénote le produit scalaire et la norme associée.
La distance du cosinus est toujours comprise entre -1 et +1 et peut être reliée intuitivement avec la notion de corrélation de la manière suivante :
- plus deux termes sont similaires et plus ils leur apparence dans un même document est corrélée. Ceci se traduit géométriquement par être "colinéaires", c'est à dire par un angle faible entre eux et donc un cosinus proche de +1 ou -1 ;
- inversement, deux termes non similaires ont tendance a avoir des apparitions décorrélées. Autrement dit, ils sont "orthogonaux" géométriquement et leur cosinus sera proche de 0.
Notons cependant que "similaire" ici ne veux pas dire que leur sens est proche mais que leur occurences est corrélés. Les termes eux-mêmes pouvant être synonymes, antonymes ou encore aller de paire dans le corpus considéré (ex. "chien" peut être similaire à "alarme" dans un contexte de sûreté et similaire à "compagnion" dans un corpus sur les animaux domestiques). Il faut garder à l'esprit que cette démarche vise moins à établir des synonymes entre les termes qu'à déterminer si deux documents peuvent être considérés comme "proches" d'un point de vue sémantique.
Limitations de la distance du cosinus
Cette distance est parmi les plus utilisées, cependant elle présente tout de même quelques limitations.
Une des limites de la distance du cosinus est qu'elle ne tient pas compte de la possibilité d'utiliser des synonymes lors de la rédaction du corpus. Si un texte n'utilise que le mot "chien" et un autre que le mot "canidé", leur distance sera considérée comme grande. Ce point peut être résolu en faisant appel à des modifications du corpus comme avec la méthode LSI.
Une limitation plus importante de cette méthode, comme mentionné par Senellart et Blondel est que le modèle mathématique sous-jacent repose sur l'hypothèse d'un espace orthogonal, ce qui implique les termes soient globalement répartis uniformément les uns par rapport aux autres dans le corpus, ce qui est rarement le cas puisque le corpus est en principe une collection de document partageant des caractéristiques communes (et donc des similarités).
Autres distances possibles
Il est également possible de définir d'autre distances comme
- la distance de cluster proposée par Chen et Lynch (1972) qui est une distance asymétrique (si i et similaire à j, cela ne veut pas dire que j est similaire à i) et définie par
où désigne la norme de i, c'est-à-dire la somme de la valeur absolue des coordonnées de i.
- les mesures de Jaccard définies par
par exemple, on peut définir une mesure qui soit le quotient du nombre de fois où i et j apparaissent dans la même phrase divisé par le nombre de fois où i et j apparaissent (ensemble ou non).
Autres bases possibles pour la classification
D'autres bases existent pour la classification que la définition d'une distance poiur définir la similarité entre deux termes. On peut voir à ce sujet Aggarwal & Zhai qui distinguent
- la méthode LSI (Latent Semantic Indexing) qui cherche a grouper les termes synonymes avant la classification. A ce sujet, voir Senellart & Blondel in Berry & Castellanos (2007), p25
- la méthode NMF (Non-negative Matrix Factorisation) dont le but est d'extraire de la matrice termes-documents un ensemble plus restreint de caractéristiques sur lesquelles seront appliqué la classification.
- les méthodes basées sur l'entropie
ou encore Pons & Latapy au sujet des marches aléatoires.
Méthodes de regroupement
Regroupement Hiérachique
Single linkage
Average linkage
Complete linkage
Regroupement basés sur la distance
k-mean
k-medoid
Autres méthodes
Méthodes hybrides : Eclater et regrouper (Scatter-Gather)
D'autres méthodes existent dont la mise en oeuvre peut être plus complexe comme
- le Buckshot qui cherche à améliorer les algorithmes de type k-means en sélectionnant graines au lieu de puis les fusionnent en k graines ;
- la Fractionalisation qui répartit le corpus en sous-corpus de tailles réduites, réalise une agglomération des corpus pour en réduire le nombre puis classifie le corpus réduit.
Méthodes basées sur la fréquence des termes D'autres méthodes existent encore, basées entre autres sur la fréquence de présence des termes dans les documents. Pour de plus amples informations sur ces méthodes, voir [1]
Références
- Berry, M. & Castellanos, M. (2007) Survey of Text Mining: Clustering, Classification, and Retrieval, Second Edition PDF
- Aggarwal, C. & Zhai C. (2012). A Survey of Clustering Algorithms, in Mining Text Data, Springer. ch4 PDF
- Grivel, L. (s.d.) Outils de classification et de catégorisation pour la fouille de textes. http://www.irit.fr/SDC2006/cdrom/contributions/Grivel-isko-sdc.pdf PDF]
- Feinerer, I., Hornik, K. & Meyer, D. (2008). Text Mining Infrastructure in R. Journal of Statistical Software, 25. PDF
- Pons, P. & Latapy, M. (2005) Computing communities in large networks using random walks PDF
- Chen and Lynch (1992). Automatic construction of networks of concepts characterizing document databases. IEEE Transactions on Systems, Man and Cybernetics, 22(5):885–902.
Manuel R
Références informelles
- Beloshytski, A. TextMining with R