« Computation avec JavaScript » : différence entre les versions
Aucun résumé des modifications |
|||
| Ligne 13 : | Ligne 13 : | ||
== Introduction == | == Introduction == | ||
Cette page complémente le [[Tutoriel JavaScript de base]] avec l'analyse d'exemples d'algorithmes en [[JavaScript]]. Les exemples sont censés montrer des petites applications ou des simples jeux, mais sans l'interface utilisateur qui est traitée plutôt dans le [[Tutoriel JavaScript côté client]] et, surtout, dans la page [[Interactivité avec JavaScript]] qui utilise une approche avec des exemples expliqués de manière détaillée. | Cette page complémente le [[Tutoriel JavaScript de base]] avec l'analyse d'exemples d'[[algorithme|algorithmes]] en [[JavaScript]]. Les exemples sont censés montrer des petites applications ou des simples jeux, mais sans l'interface utilisateur qui est traitée plutôt dans le [[Tutoriel JavaScript côté client]] et, surtout, dans la page [[Interactivité avec JavaScript]] qui utilise une approche avec des exemples expliqués de manière détaillée. | ||
L'objectif de cet article est de montrer, avec des exemples pratiques, comment on peut combiner les éléments fondamentaux de la programmation pour construire une solution automatisée qui permet d'atteindre un objectif déterminé, que ce soit un petit jeu ou du traitement de l'information. | L'objectif de cet article est de montrer, avec des exemples pratiques, comment on peut combiner les éléments fondamentaux de la programmation pour construire une solution automatisée qui permet d'atteindre un objectif déterminé, que ce soit un petit jeu ou du traitement de l'information. | ||
| Ligne 55 : | Ligne 55 : | ||
#: Cette branche concerne tous les ''éléments'' qui peuvent faire eux-mêmes ou contribuer à exécuter des calculs. Dans le cadre de nos objectifs pour cet article, on retrouve dans cette branche les ordinateurs ou dispositifs numériques en général, les compilateurs/interprètes, ainsi que les langages de programmation. | #: Cette branche concerne tous les ''éléments'' qui peuvent faire eux-mêmes ou contribuer à exécuter des calculs. Dans le cadre de nos objectifs pour cet article, on retrouve dans cette branche les ordinateurs ou dispositifs numériques en général, les compilateurs/interprètes, ainsi que les langages de programmation. | ||
Nous introduisons ces concepts très abstraits pour illustrer que les dispositifs numériques qu'on utilise aujourd'hui sont directement liés à cette théorie, car on fait remonter typiquement la naissance de l'informatique (ou Computer Science) aux travaux de [https://fr.wikipedia.org/wiki/Alonzo_Church Alonzo Church] et [https://fr.wikipedia.org/wiki/Alan_Turing Alan Turing] à propos du '''problème de la décision''' (Turing, 1936). En essayant de simplifier au maximum ces concepts, il s'agit de la possibilité de créer un système mécanique qui soit capable de déterminer si la solution trouvée à un problème à travers des algorithmes est correcte. La '''machine de Turing''', un modèle théorique de calculateur, est le résultat de cette tentative et elle est à la base des dispositifs numériques qu'on utilise aujourd'hui. La plupart de ces dispositifs, en effet, est basée sur ce qu'on appelle l''''architecture de Von Neumann''', d'après le mathématicien [https://fr.wikipedia.org/wiki/John_von_Neumann John von Neumann], qui s'est inspiré des travaux de Turing. | Nous introduisons ces concepts très abstraits pour illustrer que les dispositifs numériques qu'on utilise aujourd'hui sont directement liés à cette théorie, car on fait remonter typiquement la naissance de l'informatique (ou Computer Science) aux travaux de [https://fr.wikipedia.org/wiki/Alonzo_Church Alonzo Church] et [https://fr.wikipedia.org/wiki/Alan_Turing Alan Turing] à propos du '''problème de la décision''' (Turing, 1936). En essayant de simplifier au maximum ces concepts, il s'agit de la possibilité de créer un système mécanique qui soit capable de déterminer si la solution trouvée à un problème à travers des [[algorithme|algorithmes]] est correcte. La '''machine de Turing''', un modèle théorique de calculateur, est le résultat de cette tentative et elle est à la base des dispositifs numériques qu'on utilise aujourd'hui. La plupart de ces dispositifs, en effet, est basée sur ce qu'on appelle l''''architecture de Von Neumann''', d'après le mathématicien [https://fr.wikipedia.org/wiki/John_von_Neumann John von Neumann], qui s'est inspiré des travaux de Turing. | ||
=== Définition informelle pour les objectifs de cet article === | === Définition informelle pour les objectifs de cet article === | ||
| Ligne 141 : | Ligne 141 : | ||
== Exemples étape par étape == | == Exemples étape par étape == | ||
Dans cette section, nous allons analyser de manière détaillée quelques exemples de code où des principes de computation sont adoptés pour faciliter ou améliorer les instructions passées à l'interprète JavaScript. Les exemples sont souvent retravaillés pour montrer que la construction d'un algorithme n'est pas une démarche qui se fait du premier coup ; au contraire, il faut souvent revoir le code, parfois même le refaire. | Dans cette section, nous allons analyser de manière détaillée quelques exemples de code où des principes de computation sont adoptés pour faciliter ou améliorer les instructions passées à l'interprète JavaScript. Les exemples sont souvent retravaillés pour montrer que la construction d'un [[algorithme]] n'est pas une démarche qui se fait du premier coup ; au contraire, il faut souvent revoir le code, parfois même le refaire. | ||
Voici un aperçu des exemples et des principes que nous allons voir : | Voici un aperçu des exemples et des principes que nous allons voir : | ||
Version du 14 octobre 2022 à 11:12
| Initiation à la pensée computationnelle avec JavaScript | |
|---|---|
| Module: Concepts de base de JavaScript ▬▶ | |
| ◀▬▬▶ | |
| ⚐ à finaliser | ☸ débutant |
| ⚒ 2022/10/14 | |
| Voir aussi | |
| Catégorie: JavaScript | |
Introduction
Cette page complémente le Tutoriel JavaScript de base avec l'analyse d'exemples d'algorithmes en JavaScript. Les exemples sont censés montrer des petites applications ou des simples jeux, mais sans l'interface utilisateur qui est traitée plutôt dans le Tutoriel JavaScript côté client et, surtout, dans la page Interactivité avec JavaScript qui utilise une approche avec des exemples expliqués de manière détaillée.
L'objectif de cet article est de montrer, avec des exemples pratiques, comment on peut combiner les éléments fondamentaux de la programmation pour construire une solution automatisée qui permet d'atteindre un objectif déterminé, que ce soit un petit jeu ou du traitement de l'information.
Avant de voir les exemples, nous allons définir très superficiellement le concept de computation et le mettre en relation avec la programmation. Ensuite, nous verrons de manière technique comment se passe la computation/évaluation du code en JavaScript.
Prérequis
Pour lire cet article, des notions sur les éléments fondamentaux de la programmation, illustrés dans l'introduction à la programmation, peuvent faciliter la compréhension à la fois des termes techniques et des concepts auxquels ils se réfèrent. Une exposition au moins à la syntaxe de JavaScript, disponible dans la deuxième section du Tutoriel JavaScript de base, est également conseillée, même si des références croisées à cette page sont disponibles surtout dans les premiers exemples.
- (lire les conseils de lecture sur cette page)
Exemples traités dans l'article
prompt() pour simuler des inputs différents, même si cet élément est disponible exclusivement dans le navigateur.Les exemples sont censés fonctionner dans tous les environnements où JavaScript peut être exécuté et par conséquent ils peuvent être testés directement dans la console du navigateur comme il a été suggéré dans le Tutoriel JavaScript de base. La seule exception concerne l'utilisation dans certains exemples de l'élément prompt() qui appartient à l'environnement JavaScript côté client, mais qui nous servira pour simuler facilement des inputs différents que vous aurez à fournir à travers la fenêtre.
Tous les exemples illustrés dans cette page sont disponibles dans un repository de GitHub. Ils suivent une numérotation qui sera utilisée pour les référencer également dans le texte, par exemple: 00-01.
- pour télécharger les fichiers ou voir le code source complet
Pour des raisons d'espace, souvent seules les parties du code indispensables à la compréhension du concept expliqué seront affichées. La référence aux lignes intéressées sera fournie pour pouvoir se repérer dans le code source.
Définition de computation
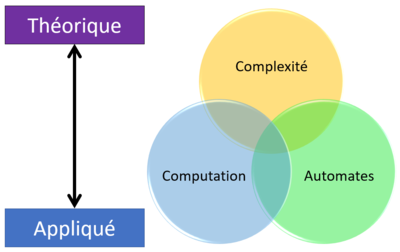
Pour définir la computation, nous allons introduire brièvement et de manière très superficielle la théorie de la computation (Sipser, 2012). Cette théorie s'intéresse à la question fondamentale de savoir quelles sont les possibilités et par conséquent les limites (ou non possibilités) des calculateurs (Sipser, 2012). Par calculateurs il faut entendre tout système, physique ou théorique, qui permet de faire des calculs. En effet, cette théorie peut être vue sur un continuum entre deux pôles :
- le pôle théorique qui est plus étroitement lié à la logique et aux mathématiques ;
- le pôle appliqué qui est plus proche des objectifs de cette page et s'occupe d'implémenter physiquement les aspects théoriques dans des machines ou dans des programmes.
La théorie de la computation émerge de l'interaction de trois sous-théories (Sipser, 2012) :
- La théorie de la complexité
- Cette branche analyse les raisons pour lesquelles certains problèmes sont faciles à résoudre et d'autres sont plus complexes.
- La théorie de la computation
- Cette branche s'intéresse aux problèmes de manière dichotomique, en essayant de déterminer quels problèmes ont une solution possible et ceux qui, au contraire, ne peuvent pas être résolus.
- La théorie des automates
- Cette branche concerne tous les éléments qui peuvent faire eux-mêmes ou contribuer à exécuter des calculs. Dans le cadre de nos objectifs pour cet article, on retrouve dans cette branche les ordinateurs ou dispositifs numériques en général, les compilateurs/interprètes, ainsi que les langages de programmation.
Nous introduisons ces concepts très abstraits pour illustrer que les dispositifs numériques qu'on utilise aujourd'hui sont directement liés à cette théorie, car on fait remonter typiquement la naissance de l'informatique (ou Computer Science) aux travaux de Alonzo Church et Alan Turing à propos du problème de la décision (Turing, 1936). En essayant de simplifier au maximum ces concepts, il s'agit de la possibilité de créer un système mécanique qui soit capable de déterminer si la solution trouvée à un problème à travers des algorithmes est correcte. La machine de Turing, un modèle théorique de calculateur, est le résultat de cette tentative et elle est à la base des dispositifs numériques qu'on utilise aujourd'hui. La plupart de ces dispositifs, en effet, est basée sur ce qu'on appelle l'architecture de Von Neumann, d'après le mathématicien John von Neumann, qui s'est inspiré des travaux de Turing.
Définition informelle pour les objectifs de cet article
La théorie de la computation dépasse largement les objectifs de cet article mais on peut néanmoins s'en servir pour formuler une définition informelle de la computation plus adaptée au contexte. On peut considérer le développement comme un processus qui consiste à :
- Réduire la complexité d'un problème ou d'un besoin, par exemple une application interactive qui favorise l'apprentissage d'une langue étrangère, à une suite d'instructions automatisées.
- Traduire ces instructions en code JavaScript, afin que l'interprète puisse les computer de manière correspondante aux attentes.
Pour atteindre cet objectif, il faut déployer les principes de la pensée computationnelle - décomposition, reconnaissance de pattern, abstraction et construction d'algorithmes - car l'interprète n'accepte que des instructions très simples. S'il existait une fonction JavaScript déjà disponible, du type
Learn('Italiano') = Io parlo perfettamente l'italiano
on l'utiliserait ! Cela n'est pas le cas et par conséquent il faut avoir recours aux blocs constitutifs de la programmation (variables, boucles, structures de contrôle, ...) qui sont construits de manière flexible afin de pouvoir répondre à la plupart des exigences en termes computationnels.
La traduction en code JavaScript nécessite deux connaissances qui s'influencent mutuellement dans un cycle itératif :
- Savoir réduire toutes les fonctionnalités qui composent l'application dans du pseudo code
- Le pseudo code est une forme hybride entre le langage naturel des humains et le code d'une machine qui permet de décrire le fonctionnement d'un programme de manière plutôt générale. Des phrases en pseudo code peuvent ressembler à :
- Pose des questions tant que l'apprenant n'a pas eu au moins 10 réponses correctes
- Affiche une réponse correcte et 4 distracteurs
- Si le score est supérieur à 100, passe au niveau supérieur
- Le pseudo code est également un bon moyen pour commenter son propre code, surtout pour les débutants.
- Le pseudo code est une forme hybride entre le langage naturel des humains et le code d'une machine qui permet de décrire le fonctionnement d'un programme de manière plutôt générale. Des phrases en pseudo code peuvent ressembler à :
- Savoir passer du pseudo code au code JavaScript
- Le pseudo code, en tant que méta-algorithme, ne peut pas être exécuté par une machine. Il est donc nécessaire de maîtriser les règles syntaxiques et d'exploiter les éléments propres à JavaScript pour obtenir les computations/instructions du pseudo code.
Cet article se pose l'objectif très ambitieux de formuler des exemples qui permettent d'améliorer les connaissances sur les deux fronts même si le focus est plutôt axé sur le deuxième aspect, plus technique. Bien entendu, cet objectif peut s'atteindre seulement à travers l'interaction entre pratique et connaissance du langage. Cette connaissance passe également par la compréhension de la façon dont le code est évalué. Pour cette raison, nous illustrerons dans la section suivante le fonctionnement de l'interprète JavaScript.
Principe technique de la computation avec JavaScript
Dans cette partie de l'article, nous aborderons le fonctionnement de l'évaluation du code JavaScript par l'interprète. Avec des exemples très simples, nous illustrerons ce qu'on appelle le parsing, c'est-à-dire l'analyse syntaxique appliquée au code source. En effet, les langages de programmation appliquent eux-mêmes, par nécessité, les principes de décomposition et reconnaissance de pattern. Le code source est décomposé en une série de petites instructions, et ces instructions doivent suivre des règles syntaxiques : l'utilisation de mots que l'interprète reconnaît dans un ordre qu'il arrive à comprendre. Pour une explication plus approfondie de ce mécanisme, voir Simpson (2015).
Fonctionnement d'une assignation de valeur à une variable
Commençons par analyser une simple assignation d'une valeur littérale à une variable :
var language = "JavaScript";
Cette simple instruction se traduit en langage courant/pseudo code de la manière suivante :
- Crée une boîte avec l'étiquette language
- Mets à l'intérieur le mot JavaScript.
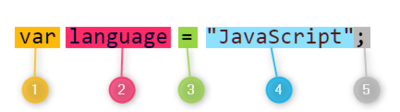
Pour l'interprète cette simple instruction se compose en réalité de 5 passages :
- Reconnaît le mot
var. Un nom de variable est attendu. - Reconnaît le nom de variable
languagecomme un nom qui respecte les règles syntaxiques des noms des variables. Un symbole d'affection à ce point est optionnel. - Reconnaît le symbole d'affection
=. Une expression qui détermine une valeur est attendue. - Reconnaît l'expression
"JavaScript"comme une suite de caractères composée par les caractères J, a, v, a, S, c, r, i, p, t. - Reconnaît le
;qui détermine la fin d'une instruction.
À ce point, l'interprète sait qu'il peut créer dans la logique de l'application une référence symbolique identifiable avec le nom language. Chaque fois qu'il reconnaît à nouveau ce nom, la suite de caractère JavaScript sera utilisé à sa place.
Évaluation d'une expression après le symbole d'affectation


Si on modifie légèrement le code, tout simplement en divisant le mot JavaScript en deux parties - "Java" et "Script" - et en utilisant l'opérateur + pour les concaténer, la situation change :
var language = "Java" + "Script";
À ce moment, l'évaluation du code reflète les étapes vue plus haut, mais jusqu'à l'étape 3. À partir de l'étape 4, les choses se modifient, parce que si on avait gardé le même principe que l'exemple précédent, on aurait comme résultat l'affectation de la variable language à la suite de caractères Java et dans un deuxième temps on ajoute Script. Mais dans ce cas lorsqu'on utiliserait language dans la suite du code on ferait référence seulement à Java et non pas à JavaScript.
Ainsi l'évaluation du code ne suit pas l'ordre précis des mots mais évalue des patterns qui peuvent avoir des priorités différentes. Dans ce cas, tout ce qui se passe sur la droite du symbole d'affectation = a la précédence sur l'ensemble de la ligne du code. Une fois que l'expression "Java" + "Script" a été évaluée, l'interprète retourne en arrière et affecte "JavaScript" à la variable language. Grâce à ce mécanisme, notre language sera donc JavaScript et non pas Java : un grand avantage !
Réutilisation d'une variable dans l'affectation de la même variable

L'importance de l'ordre du parsing est plus évident si on modifie l'exemple en décomposant "JavaScript" en deux variables, l'une avec la valeur "Java" et l'autre avec la valeur "Script" :
var language = "Java";
var correction = "Script";
language = language + correction;
Vous pouvez noter que pour corriger notre erreur dans l'affectation du nom du langage, à la ligne trois, nous faisons référence à la fausse valeur initiale, à laquelle on ajoute la correction. Grâce au mécanisme de parsing, cette expression est évaluée en amont, et donc on peut très bien associer cette nouvelle valeur computée à la variable language elle-même.
Exemples étape par étape
Dans cette section, nous allons analyser de manière détaillée quelques exemples de code où des principes de computation sont adoptés pour faciliter ou améliorer les instructions passées à l'interprète JavaScript. Les exemples sont souvent retravaillés pour montrer que la construction d'un algorithme n'est pas une démarche qui se fait du premier coup ; au contraire, il faut souvent revoir le code, parfois même le refaire.
Voici un aperçu des exemples et des principes que nous allons voir :
- Manipulation des valeurs d'une variable
- À travers le score à un test d'apprentissage imaginaire, nous illustrerons l'utilisation des variables pour stocker, récupérer et modifier une valeur
- Comparaison et structures de contrôle
- Une série de petits exemples montrent comment utiliser des éléments computationnels pour comparer des valeurs, par exemple la réponse d'un utilisateur
- Génération d'éléments aléatoires et randomisation
- Nous présentons une série de petites applications/jeux qui s’appuient sur des éléments générés aléatoirement pour rendre l'application plus intéressante et moins répétitive ;
- Tic-tac-toe (avancé)
- Pour terminer les exemples, nous proposons une application complète qui permet de jouer au jeu tic-tac-toe (ou morpion) dans la console du navigateur. Le code dépasse le niveau débutant de l'article, mais vous pouvez néanmoins tester l'application pour vous rendre compte de la complexité de coder une application à l'apparence simple.
Nous conseillons de tester et jouer avec le code directement dans la console de votre navigateur. Dans la plupart des navigateurs, il suffit de cliquer sur F12 pour l'ouvrir. Des informations plus détaillées sur la console sont disponibles dans le tutoriel JavaScript de base.
Manipulation des valeurs d'une variable
Déclaration d'une variable
Dans cet exemple, nous allons imaginer de simples algorithmes qui permettent de modifier le score, par exemple à un test d'apprentissage. Pour ce faire, nous allons d'abord créer une référence symbolique au score à travers la déclaration d'une variable comme dans le fichier 01-01 :
var score = 0;
La décision de faire démarrer le score à 0 est tout à fait conventionnelle, on pourrait imaginer n'importe quelle valeur de départ. Le choix du nom de la variable est également arbitraire, mais ceci nous permet d'avoir une idée précise de l'utilité de la variable : elle sert justement à stocker le score actuel de l'apprenant.
Modification de la valeur à travers une fonction
Nous allons maintenant modifier la valeur initiale du score avec une fonction. Idéalement, cette fonction devrait être appelée chaque fois que l'apprenant donne une réponse correcte. Voici le code de l'exemple 01-02 :
var score = 0;
//Declare the function
function incrementScore() {
//increment the score
score = score + 1;
}
//Use the function three times
incrementScore(); //--> score = 1
incrementScore(); //--> score = 2
incrementScore(); //--> score = 3

Cet exemple très simple nous permet cependant de voir qu'on peut à la fois lire et modifier la valeur de la variable score à l'intérieur de la fonction incrementScore(). Ce principe s'appelle en termes informatiques Lexical Scope. Le scope, ou portée en français, détermine le lien entre une variable et sa valeur dans le bout de code dans laquelle elle est utilisée. Une fonction en JavaScript est considérée comme un bout de code à part et a donc son propre scope. Cependant, grâce au mécanisme du lexical scope, la fonction incrementScore() a accès à la variable score pour deux raisons :
- Parce que dans notre cas
var scorea été déclarée dans le global scope (c'est-à-dire le niveau supérieur du code) et donc elle sera accessible dans toutes les fonctions, quel que soit le niveau d'emboîtement où elles ont été déclarée. On peut en effet déclarer une fonction à l'intérieur d'une autre fonction, etc. - Même si cela n'avait pas été le cas, la variable
scoreet la fonctionincrementScore()ont été définies au même niveau du scope.
Comprendre le scope est l'un des challenges les plus ambitieux dans la programmation en JavaScript, mais au moins une compréhension superficielle permet d'éviter des erreurs, surtout au niveau des attentes d'avoir accès à la valeur d'une variable quand en réalité on ne l'a pas.
Donc, comme illustré sur la figure sur la droite, notre fonction incrementScore() peut :
- D'abord lire la valeur actuelle de
scoreet l'incrémenter d'une unité - Associer la nouvelle valeur à la variable elle-même
Utiliser un argument pour rendre la fonction plus flexible
On peut très bien imaginer que notre test d'apprentissage propose des questions qui diffèrent dans la difficulté, et sont par conséquent associées à des incrémentations différentes. On peut donc modifier notre fonction incrementScore() en utilisant un argument qui détermine le nombre de points à ajouter. Voici le code de l'exemple 01-03 :
var score = 0;
//Declare the function and accept an argument as number of points to add
//In this way we have a more flexible function
function incrementScoreBy(points) {
//increment the score
score = score + points;
}
//Use the function three times
incrementScoreBy(5); //--> score = 5
incrementScoreBy(10); //--> score = 15
incrementScoreBy(50); //--> score = 65
Par rapport à la version précédente, nous avons légèrement modifié le nom de la fonction en ajoutant le suffixe By qui suggère qu'on s'attend à un argument. Cet argument est ensuite tout simplement utilisé pour incrémenter le score du chiffre respectif.
Modifier la valeur à travers une autre fonction
Le même principe s'applique si on veut utiliser une pénalité suite à une mauvaise réponse. On pourrait imaginer d'utiliser la même fonction en passant par des nombres négatifs, mais c'est peut-être plus pratique d'avoir une deuxième fonction qu'on va appeler decrementScoreBy() et qui est ajoutée dans le code de l'exemple 01-04 :
var score = 0;
//Function to add points
function incrementScoreBy(points) {
//increment the score
score = score + points;
}
//Function to subtract points
function decrementScoreBy(points) {
//decrement the score
score = score - points;
}
//Use both functions
incrementScoreBy(20); //--> score = 20
decrementScoreBy(5); //--> score = 15
incrementScoreBy(15); //--> score = 30
decrementScoreBy(20); //--> score = 10
Déterminer la valeur de manière conditionnelle
Le mécanisme de pénalité introduit dans l'exemple précédent peut aboutir à un score négatif, ce qui est peut-être exagéré et pourrait contribuer à frustrer la personne et la faire abandonner. Donc on peut définir la règle suivante en pseudo-code :
Si le score est inférieur à 0, remet-le à 0
On implémente cette logique à l'intérieur de la fonction decrementScoreBy() dans l'exemple 01-05 :
//Function to subtract points
function decrementScoreBy(points) {
//decrement the score
score = score - points;
//At this point, check if it is below zero
if (score < 0) {
//Set it back to zero
score = 0;
}
}
//Use both functions
incrementScoreBy(20); //--> score = 20
decrementScoreBy(50); //--> score = 0
incrementScoreBy(15); //--> score = 15
decrementScoreBy(5); //--> score = 10
Avec l'ajout de ce code, le score ne pourra jamais être négatif après une pénalité. C'est important de bien noter cet aspect : le score est contrôlé seulement s'il est modifié à travers la fonction decrementScoreBy(). Si jamais d'autres fonctions devaient modifier la valeur en négatif, ce mécanisme de contrôle ne serait pas activé. Il faudrait donc à la rigueur l'implémenter aussi dans d'autres fonctions qui risquent de rendre le score négatif, ou trouver un mécanisme plus élaboré - et qui dépasse le cadre de cet article - pour contrôler le score à chaque modification, quel que soit l'endroit du code où elle a été faite.
Réduire la probabilité de faire des erreurs dans le code
Notre algorithme est déjà plus ou moins abouti en ce qui concerne sa fonction de base : augmenter ou diminuer le score en fonction des réponses de l'apprenant. La fonction decrementScoreBy() peut cependant générer une certaine confusion au sujet de la valeur à passer : faut-il passer un score positif ou négatif pour le décrémenter ?
Notre code est relativement court à présent donc en cas de doute on peut toujours contrôler et s'assurer depuis le code qu'il faut un nombre positif qui sera ensuite soustrait. Mais il est très probable que nous allons utiliser cette fonction à plusieurs reprises au fur et à mesure que notre application se complexifie. Utiliser par distraction la fonction avec un nombre négatif aurait une grave conséquence au niveau du fonctionnement du test : decrementScoreBy(-50) ferait en réalité gagner 50 points à l'apprenant !
Parmi toutes les alternative possibles, on peut identifier deux solutions à ce problème :
- Générer un message d'erreur et arrêter le script ;
- Ajouter une transformation de l'argument de sorte qu'il n'y ait pas de différence si la valeur passée est 50 ou -50
Dans l'exemple 01-06 nous avons opté pour la deuxième solution qui permet d'utiliser cette fonction en toute tranquillité (du moins lorsqu'on passe des valeurs de type number et pas d'autres !) :
//Function to subtract points
function decrementScoreBy(points) {
//Force number to be positive using Math.abs()
points = Math.abs(points);
//decrement the score
score = score - points;
//At this point, check if it is below zero
if (score < 0) {
//Set it back to zero
score = 0;
}
}
//Use both functions
incrementScoreBy(20); //--> score = 20
decrementScoreBy(-50); //--> score = 0
incrementScoreBy(15); //--> score = 15
decrementScoreBy(5); //--> score = 10
Grâce à la méthode Math.abs() qui transforme n'importe quel nombre dans son absolu - et donc positif - on peut être sûr que la valeur passée à la fonction decrementScoreBy() sera de toute manière soustraite au score total, que ce soit une valeur positive ou négative.
On pourrait se demander à ce point s'il vaut la peine d'implémenter le même contrôle également dans la fonction incrementScoreBy(), car potentiellement on pourrait avoir le mécanisme inverse :
incrementScoreBy(-50); //--> équivaut à soustraire 50 au score
Nous vous laissons considérer cet aspect et éventuellement l'aborder avec les exercices de consolidation proposés dans le point suivant.
Exercices de consolidation
Nous proposons à la suite deux exercices de consolidation des éléments traités dans ce premier exemple, un plus simple, et l'autre plus difficile.
- Simple
- Imaginez que le test est réussi si l'apprenant totalise au moins 100 points ;
- Implémentez un contrôle dans la fonction
incrementScoreBy()qui affiche un message de congratulations si ce score est atteint ou dépassé
- Plus difficile
- Imaginez un système de niveaux qui changent en fonction du score ;
- Chaque niveau est représenté par 10 points (de 0 à 10, niveau 1 ; de 11 à 20, niveau 2 ; etc.)
- Ajoutez une variable qui tient compte du niveau
- Ajoutez des mécanismes qui modifient automatiquement le niveau en fonction de la variation du score (en positif et en négatif)
- Hint: vous pouvez utiliser la fonction
Math.ceil()de JavaScript de base qui arrondi un chiffre décimal à l'unité la plus grande (pas la plus proche), par exemple : Math.ceil(1.1) // Donne 2
- Hint: vous pouvez utiliser la fonction
Comparaison et structures de contrôle
Simple mais insuffisante structure de contrôle
Un des aspects les plus fréquents dans l'écriture d'algorithmes concerne l'évaluation d'une ou plusieurs valeurs pour déterminer si elles correspondent à un ou plusieurs critères. Cette opération est généralement exécutée à travers les différentes structures de contrôle dont on fera ici un exemple très simple avec du if ... else .... Voici le code de l'exemple 02-01 qui vous demande de répondre à une question à travers un prompt() :
var reply = prompt("What programming language is used in this article?");
//Check the answer
if (reply == "JavaScript") {
console.log("Yes, JavaScript is the right answer");
} else {
console.log("Sorry,", reply, "is not the right answer!");
}
Ce bout de code évalue la réponse donnée et la compare avec la suite de caractères JavaScript. Il est donc nécessaire qu'il y ait une correspondance exacte avec le mot, c'est-à-dire que les réponses suivantes ne soient pas évaluées en tant que true :
- javascript
- Javascript
- javaScript
- ...
Selon la précision demandée par votre dispositif pédagogique, ceci peut-être intentionnel, mais souvent on peut laisser une certaine flexibilité surtout sur des aspects marginaux comme la casse.
Rendre deux suites de caractères comparables
Une possible solution pour augmenter la flexibilité de notre exemple précédent consiste à utiliser la stratégie de la pensée computationnelle équivalente à la reconnaissance de patterns. En effet, JavaScript et javascript (ou JaVaScRiPt et ainsi de suite) partagent toutes les mêmes lettres mais avec des casses différentes. On peut donc imaginer de baser notre comparaison entre des suites de caractères qui ne présentent que des lettres minuscules. C'est ce qui est fait dans le code 02-02 :
var givenAnswer = prompt("What programming language is used in this article?");
var correctAnswer = "JavaScript";
//Check the correctAnswer
if (givenAnswer.toLowerCase() == correctAnswer.toLowerCase()) {
console.log("Yes,", correctAnswer, "is the right answer");
} else {
console.log("Sorry,", givenAnswer, "is not the right answer");
}
Grâce à la méthode .toLowerCase() associée à une suite de caractères, tout caractère contenu dans la suite est transformé dans l'équivalent en minuscules. On utilise donc les deux versions transformées à la fois de la réponse donnée et de la réponse attendue pour évaluer la comparaison. La transformation de la réponse attendue nous permet, par la suite, d'afficher la forme correcte "JavaScript" dans le feedback.
Améliorer ultérieurement la comparaison
Nous avons déjà rendu notre comparaison plus flexible, mais il y a encore la possibilité que l'utilisateur mette un ou plusieurs espaces avant ou après la réponse :
- " JavaScript"
- "JavaScript "
Pour l'interprète, ces deux suites de caractères ne sont pas égaux à "JavaScript" donc toute réponse qui est entourée par des espaces sera considérée fausse par notre algorithme. On peut donc améliorer ultérieurement notre script pour être encore plus flexible, en utilisant la méthode .trim() qui enlève justement les espaces avant ou après une suite de caractères. Voici le code de l'exemple 02-03 :
var givenAnswer = prompt("What programming language is used in this article?");
var correctAnswer = "JavaScript";
function isGivenAnswerCorrect(given, correct) {
var given = given.toLowerCase().trim();
var correct = correct.toLowerCase().trim();
return given == correct;
}
//Check the correctAnswer
if (isGivenAnswerCorrect(givenAnswer, correctAnswer)) {
console.log("Yes,", correctAnswer, "is the right answer");
} else {
console.log("Sorry,", givenAnswer, "is not the right answer!");
}
En considération du fait que notre transformation sur les deux suites de caractères à comparer est plus complexe, il est en général de bonne pratique d'éviter des longues expressions à l'intérieur d'un if(...). Nous avons donc déclaré une fonction (ligne 4) qui s'occupe de la comparaison et return true si les deux suites de caractères transformées sont les mêmes ou false autrement.
Comparaison avec plusieurs valeurs possibles
Dans les cas où il existe plusieurs réponses possibles, ce serait trop long de faire une longue structure de contrôle du type :
if (givenAnswer == response1 || givenAnswer == response2 || givenAnswer == response3) { ... }
À la place, nous pouvons combiner les éléments fondamentaux du langage pour utiliser un array en tant que source des réponses possibles. Nous allons par la suite chercher dans cette liste si on trouve une correspondence. Voici le code de l'exemple 02-04 :
var possibleAnswers = ["html", "css", "javascript"];
//Question
var givenAnswer = prompt(
"Cite one of the main web technologies that compose an interactive web page"
);
//Check if the answer is in the array (if not, it return -1)
var isInArray = possibleAnswers.indexOf(givenAnswer.toLowerCase());
//Give a conditional feedback
if (isInArray < 0) {
console.log(
"Sorry, but",
givenAnswer,
"is not considered one of the main technologies"
);
} else {
console.log("Yes,", givenAnswer, "is one of the main web technologies");
}
La méthode .indexOf() permet de définir si un élément se trouve à l'intérieur d'un array. Ceci marche pour tout type de données, et donc on peut l'adapter dans la logique de notre code pour comparer si la réponse donnée fait partie de la "triade" des technologies web HTML, CSS, ou JavaScript.
Si l'élément ne se trouve pas dans l'array alors la méthode renvoie -1. Autrement, elle renvoie la position de l'élément dans l'array à partir de 0 (donc si la réponse donnée est css, la méthode indexOf() renvoie 1 car css est le deuxième élément de l'array).
Exercice de consolidation
Dans le dernier exemple, nous avons utilisé simplement la méthode .toLowerCase() pour comparer la réponse de l'utilisateur avec les éléments dans l'array. Améliorez le code de l'exemple 02-04 en utilisant la logique plus précise illustrée dans l'exemple 02-03.
Génération d'éléments aléatoires et randomisation
L'une des activités les plus fréquentes dans la computation est l'utilisation ou la génération d'éléments aléatoires. Dans les exemples de cette section nous allons construire, sur la base de la méthode Math.random() une série d'exemples qui exploitent la randomisation pour créer des petits jeux ou applications.
Génération aléatoire
JavaScript met à disposition directement à travers son API de base une méthode de l'objet Math qui permet de créer un chiffre aléatoire. C'est la méthode Math.random() illustrée dans l'exemple 03-01 :
var randomNumber = Math.random();
randomNumber sera associée aléatoirement à une valeur décimal entre 0 et 0.9999999999Quelques exemples de valeurs tirées aléatoirement :
- 0.38747943530628404
- 0.7096899421330576
- 0.45058892944245765
- 0.5323393682559765
Pile ou Face
Nous pouvons exploiter cette méthode pour créer un simple mécanisme de tirage au sort illustré dans l'exemple 03-02 :
var randomNumber = Math.random();
//Check the random number to determine heads or tails
if (randomNumber < 0.5) {
console.log("Heads");
} else {
console.log("Tails");
}
En considération du fait que Math.random() renvoie toujours un chiffre inférieur à 1, on peut diviser les probabilités d'avoir pile ou face de la manière suivante :
- Face de 0.000000.... à 0.49999... (donc < 0.5, voir ligne 4)
- Pile de 0.50000... à 0.999999....
Plusieurs tirages au sort
Nous pouvons maintenant tester notre système de tirage au sort en simulant 100 tirages grâce à une boucle de type for. Le code est illustré dans l'exemple 03-03 :
//Use a function to flip the coin
function getCoinFace() {
var randomNumber = Math.random();
//Check the random number to determine heads or tails
if (randomNumber < 0.5) {
return "Heads";
} else {
return "Tails";
}
}
//Let's use an object to stock the results
var flips = {
Heads: 0,
Tails: 0
};
//Simulate 100 flips
for (let i = 0; i < 100; i++) {
var currentFlip = getCoinFace();
flips[currentFlip]++;
}
//Log the results
console.log("Total Heads:", flips.Heads);
console.log("Total Tails:", flips.Tails);
Dans ce code nous avons :
- Adapté le code de l'exemple pour créer une fonction qui renvoie Heads or Tails (ligne 2-11)
- Créer un objet
flipsqui va contenir le nombre de flips.Heads or flips.Tails. Au début les deux compteurs sont à 0 (lignes 14-17) - Simulé 100 tirages à travers une boucle for (lignes 20-23)
C'est le contenu de la boucle qui nous intéresse particulièrement. Le mécanisme est assez simple :
//Simulate 100 flips
for (let i = 0; i < 100; i++) {
var currentFlip = getCoinFace();
flips[currentFlip]++;
}
Dans ce bout de code :
- D'abord, nous appelons la fonction
getCoinFace()pour savoir si le résultat est Heads or Tails. - Ensuite, nous exploitons le fait que les objets peuvent être maniés également avec la notation de type array selon la quelle :
flips.Headsest équivalente àflips[Heads]flips.Tailsest équivalente àflips[Tails]
De ce fait, lorsque nous utilisons la notation flips[currentFlip]++ nous allons incrémenter le compteur flips[Heads] ou flips[Tails] selon ce qui a été renvoyé par la fonction getCoinFace(). C'est une version raccourcie du code suivant :
var currentFlip = getCoinFace();
if(currentFlip == "Heads") {
flips.Heads++;
} else {
flips.Tails++
}
À la fin du script, le résultat de la simulation est affiché à la console. Un des outputs possibles de ce script est le suivant :
Total Heads: 46 Total Tails: 54
Lancer un dé
Jusqu'à présent, nous avons utilisé la valeur aléatoire générée à travers Math.random() telle qu'elle était, sans aucune transformation. Dans l'exemple 03-04, nous allons nous servir encore une fois de cette méthode, mais pour récupérer un chiffre aléatoire entre 1 et 6 pour simuler le lancer d'un dé. Voici le code de l'exemple qui simule une partie de dé entre l'utilisateur et l'ordinateur :
//Create a function that simulate a dice
function rollDice() {
//Return number from 1 to 6
return Math.floor(Math.random() * 6 + 1);
}
//Keep track of the score
var scores = {
you: 0,
computer: 0,
draws: 0
};
//Create a function that print the current score upon request
function whatIsTheScore() {
console.log("******************");
console.log("You have", scores.you, "points");
console.log("The computer has", scores.computer, "points");
console.log("Number of draws:", scores.draws);
console.log("******************");
}
//Create a function that simulate a game
function play() {
var yourResult = rollDice();
var computerResult = rollDice();
//Check the result
if (yourResult > computerResult) {
scores.you++;
console.log("You won", yourResult, "to", computerResult);
} else if (yourResult < computerResult) {
scores.computer++;
console.log("The computer won", computerResult, "to", yourResult);
} else {
scores.draws++;
console.log("It's a draw", yourResult, "-", computerResult);
}
//Print the current score
whatIsTheScore();
}
La logique de l'application est assez similaire à l'exemple précédent, si ce n'est le fait que cette fois-ci nous voulons des chiffres aléatoires bien précis, car nous voulons simuler les 6 faces d'un dé. Pour obtenir ceci nous avons créé une fonction qui transforme le chiffre aléatoire de cette manière :
Math.floor(Math.random() * 6 + 1);
Cette manipulation s'explique par les étapes suivantes :
- Calcule un chiffre aléatoire entre 0 et 0.9999... avec
Math.random- E.g. 0.430566161365064
- Multiplie ce chiffre par le maximum des chiffres qu'on veut obtenir, c'est-à-dire 6.
- 0.430566161365064 * 6 = 2.583396968190384
- Ajoute le minimum qu'on veut obtenir, c'est-à-dire 1
- 2.583396968190384 + 1 = 3.583396968190384
- Utilise
Math.floor()pour "baisser" tout nombre décimal au chiffre entier précédent- Math.floor(3.583396968190384) = 3
Vous pouvez simuler de jouer votre match contre l'ordinateur en copiant tout le code de l'exemple dans votre console. Ensuite, il vous suffit de saisir le code :
play();
pour simuler une manche et voir le score se modifier en correspondance du résultat obtenu.
Élément aléatoire dans un array
On peut utiliser la génération d'un chiffre entier aléatoire pour récupérer un élément d'un array. Ce mécanisme exploite tout simplement l'index d'un array du type :
var courses = ['STIC I', 'STIC II', 'STIC III', 'STIC IV'];
courses[1]; //--> STIC II
courses[3]; //-->STIC IV
On peut par conséquent générer un chiffre aléatoire comme on a fait pour le lancer de dé dans l'exemple précédent, mais au lieu de générer un chiffre entre 1 et 6, il faudra générer un chiffre entre 0 et la longueur totale de l'array. Le code de l'exemple 03-05 utilise ce principe pour poser aléatoirement une question à l'utilisateur :
var quiz = [
{
country: "Switzerland",
capital: "Bern"
},
{
country: "France",
capital: "Paris"
},
{
country: "Italy",
capital: "Rome"
}
];
//Create a function that randomly ask what is the capital of ...
function randomQuestion() {
//We generate a random number from 0 to the number of elements in the quiz
var randomNumber = Math.floor(Math.random() * quiz.length);
//Retrieve the current country and capital
var currentCountry = quiz[randomNumber].country;
var currentCapital = quiz[randomNumber].capital;
//Prompt the question
var givenAnswer = prompt("What is the capital of " + currentCountry + "?");
//Check the answer
if (givenAnswer.toLowerCase() == currentCapital.toLowerCase()) {
console.log("Yes, the capital of", currentCountry, "is", currentCapital);
} else {
console.log("Nope, the capital of", currentCountry, "is", currentCapital);
}
}
Le code de cet exemple s'explique de la manière suivante :
- D'abord, nous avons créé un array avec à l'intérieur trois objets avec les propriétés
countryetcapital(lignes 1-14) - Une fonction est déclarée pour qu'on puisse poser une question juste en appelant cette fonction (lignes 17-33)
- À l'intérieur de cette fonction, on génère un chiffre aléatoire entre 0 et
quiz.length, de cette manière notre fonction peut s'adapter si on veut ajouter par la suite d'autres countries/capitals (ligne 19) - On utilise ce chiffre comme index pour récupérer la nation et la capitale dans l'array d'objets (lignes 21-22)
var currentCountry = quiz[randomNumber].country;, par exemple quiz[0].country sera Switzerlandvar currentCapital = quiz[randomNumber].capital;, par exemple quiz[0].capital sera Bern
- La suite du code réutilise des concepts vus dans les exemples précédents pour poser la question et évaluer la réponse donnée
Pour tester cet exemple, copiez tout le code dans la console et ensuite saisissez la commande randomQuestion().
Exercices de consolidation
- Simple
Modifiez l'exemple 03-05 en ajoutant d'autres nations/capitales pour avoir plus de choix dans les questions aléatoires.
- Plus difficile
Complexifiez la logique de l'exemple 03-04 pour faire ainsi que :
- le jeu s'arrête lorsque le joueur ou l'ordinateur comptabilise 5 victoires/points ;
- un message de félicitations s'affiche en fonction du gagnant ;
- le jeu puisse redémarrer à nouveau ;
Tic-tac-toe (avancé)
Pour terminer nos exemples, nous proposons une application complète à utiliser toujours en ligne de commande, qui simule le jeu tic-tac-toe (ou jeu du morpion). Cet exemple reprend les concepts théoriques illustrés dans l'Introduction à la programmation, plus précisément dans la partie pragmatique sur les fonctions.
Le code utilisé dépasse le niveau débutant de l'article et nous le proposons plutôt pour trois raisons :
- Cela donne une idée concrète de la complexité nécessaire pour développer un jeu apparemment très simple ;
- Vous avez une référence à consulter dans le futur lorsque vous progressez avec la compréhension du code ;
- Les plus ambitieux peuvent essayer de le développer par eux-mêmes et confronter ensuite les deux codes car il n'y a jamais qu'une seule manière pour obtenir un résultat en programmation.
Vous pouvez tester le jeu en copiant tout le code de l'exemple 04-01 dans votre console. Pour abréger nous n'allons pas l'afficher entièrement sur la page. Vous pouvez le récupérer depuis le repository GitHub.
Ensuite, il faudra saisir les fonctions :
x(n)o(n)
où x et o représente les deux joueurs et n la case (entre 1 et 9) ou placer le symbole correspondant. Par exemple, lorsque le jeu démarre, si on saisi x(1) le résultat à la console sera le suivant :
------------- | x | - | - | ------------- | - | - | - | ------------- | - | - | - | -------------
Ensuite, si on saisi o(7) :
------------- | x | - | - | ------------- | - | - | - | ------------- | o | - | - | -------------
Une bonne manière pour développer de la pensée computationnelle est également de tester des interactions non attendues par le système et de voir comme il réagit. Par exemple vous pouvez tester x(12) ou x("9") ; ou encore essayer de ne pas respecter l'alternance des joueurs, etc.
Exercices supplémentaires
Des exercices supplémentaires sont disponibles dans le repository GitHub :
Les exercices proposent la structure des fichiers suivante :
- Examples : fichiers avec du code qui montre l'application des éléments fondamentaux de la programmation
- Hands-on : ce dossier est mis à disposition pour que vous puissiez expérimenter les exemples de votre côté (e.g. essayer de reproduire ce que vous avez vu sans faire du copier/coller)
- Tasks : ce dossier propose une série de challenges pour tester vos connaissances. Pour chaque tâche il y a l'énoncé du problème (...-challenge.js) et la solution (..-solution.js)
Les exemples varient en difficulté. Pour résoudre certains exemples le contenu de cette page n'est pas suffisant, il faut une lecture plus approfondie du Tutoriel JavaScript de base.
Conclusion
Dans cet article, nous avons très brièvement introduit le concept de computation en fonction de la théorie de la computation. Cette théorie est en effet à la base de la plupart des dispositifs numériques qu'on utilise aujourd'hui.
Ensuite, nous avons appliqué les concepts abstraits de cette théorie dans le cadre plus spécifique d'un automate, l'interprète JavaScript, qui lit et évalue du code afin de computer les outputs souhaités par le développeur. À travers une série d'exemples, nous avons proposé différents algorithmes qui nous ont permis de construire des applications ou des jeux très simples, mais pour lesquels la mobilisation de certains concepts computationnels a été nécessaire.
La capacité d'écrire du code qui fait exactement ce que l'on veut dépend de l’habileté du développeur à traduire une application complexe en instructions simples que l'interprète puisse comprendre et exécuter. Ce mécanisme est une nécessité due au fait que les machines, pour l'instant, comprennent seulement des instructions assez basiques. Ceci est à la fois une force et une limite :
- une force, parce que cela laisse énormément de liberté combinatoire aux développeurs pour créer toujours des applications différentes, plus ambitieuses, plus performantes, etc.
- une limite, car même pour créer une application à l'apparence assez simple, il faut une bonne connaissance non seulement du langage de programmation, mais également du fonctionnement de l'automate qui l'interprète.
Cette limite peut être dépassée, au moins en partie, grâce à l'utilisation de code qui a déjà été conçu pour certains objectifs, comme dans les cas des API de JavaScript (voir par exemple Interactivité avec JavaScript ou Bibliothèques JavaScript). Mais il est très improbable, voire impossible, de pouvoir disposer toujours de l'algorithme qui répond exactement à nos besoins. La capacité de bien combiner les éléments fondamentaux de la programmation devient donc fondamentale pour pouvoir bénéficier de toute la créativité que le développement met à disposition. D'ailleurs, Cormen et al. (2009, p.11) suggèrent que la création d'algorithmes reste indispensable indépendamment de la capacité des ordinateurs : « Suppose computers were infinitely fast and computer memory was free. Would you have any reason to study algorithms? The answer is yes, if for no other reason than that you would still like to demonstrate that your solution method terminates and does so with the correct answer. »
Bibliographie
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Alogrithms (3rd ed.). Cambridge, MA: MIT press. (Oeuvre très spécifique)
- Sipser, M. (2012). Introduction to the Theory of Computation (3rd ed.). Cengage Learning. (Oeuvre très spécifique)
- Simpson, K. (2015). You Don’t Know JS: Up & Going. Sebastopol, CA: O’Reilly Media.
- Turing, A. M. (1936). On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society, 230–265.
Ressources
- Vidéo sur le fonctionnement de JavaScript par Philip Roberts (en anglais, environ 25min.)