« Analyses statistiques avec R » : différence entre les versions
mAucun résumé des modifications |
|||
| (194 versions intermédiaires par 8 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
=Introduction= | {{tutoriel | ||
|fait_partie_du_cours=Tutoriels R | |||
|fait_partie_du_module=Tutoriels R | |||
|pas_afficher_sous-page=Non | |||
|page_precedente=Les données R | |||
|statut=à finaliser | |||
|voir_aussi=Introduction à la modélisation des données avec R | |||
|all_pages_module=Non | |||
|cat tutoriels=Tutoriels R | |||
}} | |||
== Introduction == | |||
Cet article fournit un tutoriel conçis sur le traitement des données numériques avec [[R]]. Une explication plus conceptuelle sur le fonctionnement de [[R]] pour les analyses est disponible dans la page [[Introduction à la modélisation des données avec R]]. | |||
== Les opérateurs arithmétiques classiques == | == Les opérateurs arithmétiques classiques == | ||
| Ligne 328 : | Ligne 32 : | ||
== Représenter des données sur R == | == Représenter des données sur R == | ||
L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : hist(), density(), lines(), boxplot(), barplot(), pie(),mosaicplot(), assocplot(), plot(), abline(), pairs(), scatterplot3d(). | L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : '''''hist(), density(), lines(), boxplot(), barplot(), pie(),mosaicplot(), assocplot(), plot(), abline(), pairs(), scatterplot3d().''''' | ||
=== Histogramme et fonction de densité === | === Histogramme et fonction de densité === | ||
L’histogramme permet de représenter la distribution d’une variable continue. Vous pouvez construire des histogrammes avec la fonction hist() : | L’histogramme permet de représenter la distribution d’une variable continue. Vous pouvez construire des histogrammes avec la fonction '''''hist()''''' : | ||
data(iris) | data(iris) | ||
hist(iris$Sepal.Length, prob = FALSE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Effectif ", col = "lightblue") # Histogramme en effectif | hist(iris$Sepal.Length, prob = FALSE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Effectif ", col = "lightblue") # Histogramme en effectif | ||
hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité | hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité | ||
La fonction density() permet d’obtenir un estimateur à noyau de la densité : | La fonction '''''density()''''' permet d’obtenir un estimateur à noyau de la densité : | ||
plot(density(iris$Sepal.Length)) | plot(density(iris$Sepal.Length)) | ||
| Ligne 343 : | Ligne 47 : | ||
hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité | hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité | ||
lines(density(iris$Sepal.Length),col="red") | lines(density(iris$Sepal.Length),col="red") | ||
[[Fichier:Histogramme densité.png|centre|vignette|Histogramme avec la densité |500px]] | |||
=== Boite à moustache === | === Boite à moustache === | ||
La boîte à moustache est une méthode rapide pour représenter et résumer le profil d’une variable continue. Pour créer une boîte à moustache utilisez la fonction boxplot() : | La boîte à moustache est une méthode rapide pour représenter et résumer le profil d’une variable continue. Pour créer une boîte à moustache utilisez la fonction '''''boxplot()''''' : | ||
A <- rnorm(1000, 100, 10) # A est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 100 et d'écart-type 10 | A <- rnorm(1000, 100, 10) # A est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 100 et d'écart-type 10 | ||
B <- rnorm(1000, 120, 20) # B est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 120 et d'écart-type 20 | B <- rnorm(1000, 120, 20) # B est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 120 et d'écart-type 20 | ||
boxplot(A, main = "Distribution des valeurs générés") | boxplot(A, main = "Distribution des valeurs générés") | ||
boxplot(list(A, B), main = "Distribution des valeurs générés" , names = c("µ = 100, sd = 10", "µ = 120, sd = 20 ")) | boxplot(list(A, B), main = "Distribution des valeurs générés" , names = c("µ = 100, sd = 10", "µ = 120, sd = 20 ")) | ||
[[Fichier:Boxplot.png|Boites à moustache des vecteurs A et B|500px|centre|vignette]] | |||
=== Diagramme en tuyaux d’orgue === | === Diagramme en tuyaux d’orgue === | ||
Le diagramme en tuyaux d’orgue permet de représenter graphiquement la distribution d'une variable discrète. Pour créer un diagramme en tuyaux d’orgue, utilisez la fonction barplot() : | Le diagramme en tuyaux d’orgue permet de représenter graphiquement la distribution d'une variable discrète. Pour créer un diagramme en tuyaux d’orgue, utilisez la fonction '''''barplot()''''' : | ||
ventes <- c(200, 102, 32, 120, 310, 152) | ventes <- c(200, 102, 32, 120, 310, 152) | ||
names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon") | names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon") | ||
barplot(ventes, main = "Diagramme des ventes", col = "lightblue") | barplot(ventes, main = "Diagramme des ventes", col = "lightblue") | ||
barplot(ventes, main = "Diagramme des ventes", col = "lightblue", horiz = TRUE) | barplot(ventes, main = "Diagramme des ventes", col = "lightblue", horiz = TRUE) | ||
[[Fichier:Barplot.png|centre|vignette|Diagramme en tuyaux d'orgue|500px]] | |||
=== Diagramme circulaire === | === Diagramme circulaire === | ||
Le diagramme circulaire permet de représenter des variables discrètes. Utilisez la fonction pie() pour construire des diagrammes circulaires : | Le diagramme circulaire permet de représenter des variables discrètes. Utilisez la fonction '''''pie()''''' pour construire des diagrammes circulaires : | ||
ventes <- c(200, 102, 32, 120, 310, 152) | ventes <- c(200, 102, 32, 120, 310, 152) | ||
names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon") | names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon") | ||
pie(ventes, main = "Diagramme des ventes", col = rainbow(length(ventes))) | pie(ventes, main = "Diagramme des ventes", col = rainbow(length(ventes))) | ||
[[Fichier:Camembert.png|vignette|Diagramme circulaire|500px|centre]] | |||
=== Diagramme empilé === | === Diagramme empilé === | ||
Le diagramme empilé permet de représenter graphiquement les effectifs d’un tableau de contingence. Le diagramme empilé s’obtient au moyen de la fonction barplot() en fournissant un objet de mode matrix : | Le diagramme empilé permet de représenter graphiquement les effectifs d’un tableau de contingence. Le diagramme empilé s’obtient au moyen de la fonction '''''barplot()''''' en fournissant un objet de mode matrix : | ||
data(HairEyeColor) | data(HairEyeColor) | ||
HairEye <- apply(HairEyeColor, c(1, 2), sum) | HairEye <- apply(HairEyeColor, c(1, 2), sum) | ||
barplot(HairEye, legend = rownames(HairEye), main = "Diagramme empilé", xlab = "Couleur des yeux") | barplot(HairEye, legend = rownames(HairEye), main = "Diagramme empilé", xlab = "Couleur des yeux") | ||
[[Fichier:Diagramme empilé.png|vignette|Diagramme empilé|500px|centre]] | |||
=== Diagrammes en mosaïque === | === Diagrammes en mosaïque === | ||
Le diagramme en mosaïque permet de représenter graphiquement les effectifs d’un tableau de contingence. De ce fait, la surface des mosaïques est proportionnelle aux effectifs observés dans les cellules du tableau de contingence. Pour créer un diagramme en mosaïque utilisez la fonction mosaicplot() : | Le diagramme en mosaïque permet de représenter graphiquement les effectifs d’un tableau de contingence. De ce fait, la surface des mosaïques est proportionnelle aux effectifs observés dans les cellules du tableau de contingence. Pour créer un diagramme en mosaïque utilisez la fonction '''''mosaicplot()''''' : | ||
mosaicplot(HairEye, main = "Diagramme en mosaïque", xlab = "Cheveux", ylab = "Yeux") | mosaicplot(HairEye, main = "Diagramme en mosaïque", xlab = "Cheveux", ylab = "Yeux") | ||
[[Fichier:Diagrammes en mosaïque.png|vignette|Diagramme en mosaïque|500px|centre]] | |||
=== Graphique d’association === | === Graphique d’association === | ||
Le graphique d’association de Cohen-Friendly indique les déviations par rapport à l’indépendance dans une table de contingence. Utilisez la fonction assocplot() pour créer un graphique d’association : | Le graphique d’association de Cohen-Friendly indique les déviations par rapport à l’indépendance dans une table de contingence. Utilisez la fonction '''''assocplot()''''' pour créer un graphique d’association : | ||
assocplot(HairEye, main = "Graphique d’association", xlab = "Cheveux", ylab = "Yeux") | assocplot(HairEye, main = "Graphique d’association", xlab = "Cheveux", ylab = "Yeux") | ||
[[Fichier:Graphique d’association.png|vignette|Graphique d’association|500px|centre]] | |||
=== Nuage des points 2D === | === Nuage des points 2D === | ||
La fonction plot() permet – entre d’autres – de représenter deux variables continues dans un plan cartésien. Exemple : | La fonction '''''plot()''''' permet – entre d’autres – de représenter deux variables continues dans un plan cartésien. Exemple : | ||
data(USArrests) | data(USArrests) | ||
plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") | plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") | ||
abline(lm(USArrests$Murder~USArrests$Assault), col = "red") | abline(lm(USArrests$Murder~USArrests$Assault), col = "red") | ||
Remarque : la fonction | Remarque : la fonction “''lm''” permet de créer des modèles linéaires (on y reviendra). | ||
[[Fichier:Nuage des points 2D.png|vignette|Nuage des points 2D|500px|centre]] | |||
=== Matrice des scatter plots === | === Matrice des scatter plots === | ||
La fonction pairs() permet de représenter un scatter plot pour chaque couple possible de colonnes d’un dataframe ou d’une matrice donnée : | La fonction '''''pairs()''''' permet de représenter un scatter plot pour chaque couple possible de colonnes d’un dataframe ou d’une matrice donnée : | ||
data <- USArrests[,c(1,2,4)] | data <- USArrests[,c(1,2,4)] | ||
pairs(data) | pairs(data) | ||
[[Fichier:Matrice des scatter plots.png|vignette|Matrice des scatter plots|500px|centre]] | |||
=== Nuage des points 3D === | === Nuage des points 3D === | ||
La fonction scatterplot3d() permet de représenter trois variables dans un espace tridimensionnel. Pour utiliser cette fonction il faut installer le package « scatterplot3d » : | La fonction '''''scatterplot3d()''''' permet de représenter trois variables dans un espace tridimensionnel. Pour utiliser cette fonction il faut installer le package « ''scatterplot3d'' » : | ||
library(scatterplot3d) | library(scatterplot3d) | ||
s3d <- scatterplot3d(USArrests$Assault, USArrests$Rape, USArrests$Murder, type= "h", highlight.3d = TRUE, angle = 45, scale.y = 0.5, pch = 20, main = "Nuage des points 3D", xlab = "Nombre d’agressions", ylab = " Nombre de viols", zlab = "Nombre d’assassinats") | s3d <- scatterplot3d(USArrests$Assault, USArrests$Rape, USArrests$Murder, type= "h", highlight.3d = TRUE, angle = 45, scale.y = 0.5, pch = 20, main = "Nuage des points 3D", xlab = "Nombre d’agressions", ylab = " Nombre de viols", zlab = "Nombre d’assassinats") | ||
s3d$plane3d(lm(USArrests$Murder ~ USArrests$Assault + USArrests$Rape)) | s3d$plane3d(lm(USArrests$Murder ~ USArrests$Assault + USArrests$Rape)) | ||
[[Fichier:Nuage des points 3D.png|vignette|Nuage des points 3D|500px|centre]] | |||
=== Corrgram === | === Corrgram === | ||
La fonction corrgram() permet de représenter graphiquement une matrice de corrélation de manière efficace. Pour utiliser cette fonction il faut installer le package « corrgram » : | La fonction '''''corrgram()''''' permet de représenter graphiquement une matrice de corrélation de manière efficace. Pour utiliser cette fonction il faut installer le package « ''corrgram'' » : | ||
library(corrgram) | library(corrgram) | ||
data(auto) | data(auto) | ||
corrgram(auto, order=TRUE, main="Auto data (PC order)") | corrgram(auto, order=TRUE, main="Auto data (PC order)") | ||
[[Fichier:Corrgram.png|vignette|Corrgram|500px|centre]] | |||
== Traitements statistiques élémentaires == | == Traitements statistiques élémentaires == | ||
L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : mean(), sd(), median(), quantile(), min(), max(), summary() et cov(). | L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : '''''mean(), sd(), median(), quantile(), min(), max(), summary()''''' et '''''cov()'''''. | ||
=== Mesures de tendance centrale, de dispersion et de position === | === Mesures de tendance centrale, de dispersion et de position === | ||
Les fonctions mean(), sd() restituent la moyenne, et respectivement l’écart-type d’un objet donné : | Les fonctions '''''mean()''''', '''''sd()''''' restituent la moyenne, et respectivement l’écart-type d’un objet donné : | ||
mean(USArrests$Murder) | mean(USArrests$Murder) | ||
sd(USArrests$Murder) | sd(USArrests$Murder) | ||
Les fonctions median() et quantile() restituent le médian et les quantiles désirées : | Les fonctions '''''median()''''' et '''''quantile()''''' restituent le médian et les quantiles désirées : | ||
median(USArrests$Murder) | median(USArrests$Murder) | ||
quantile(USArrests$Murder, c(0.25, 0.5, 0.75)) # Donne les 3 quartiles | quantile(USArrests$Murder, c(0.25, 0.5, 0.75)) # Donne les 3 quartiles | ||
quantile(USArrests$Murder, c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9)) # Donne les 9 déciles | quantile(USArrests$Murder, c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9)) # Donne les 9 déciles | ||
Les fonctions min() et max() restituent la valeur minimale et maximale d’un objet : | Les fonctions '''''min()''''' et '''''max()''''' restituent la valeur minimale et maximale d’un objet : | ||
min(USArrests$Murder) | min(USArrests$Murder) | ||
max(USArrests$Murder) | max(USArrests$Murder) | ||
| Ligne 434 : | Ligne 159 : | ||
=== Résumé statistique === | === Résumé statistique === | ||
La fonction summary() fournit une série d’information qui varie en fonction de l’objet d’input : | La fonction '''''summary()''''' fournit une série d’information qui varie en fonction de l’objet d’input : | ||
summary(iris) | summary(iris) | ||
summary(USArrests) | summary(USArrests) | ||
| Ligne 440 : | Ligne 165 : | ||
=== Matrice de variance-covariance === | === Matrice de variance-covariance === | ||
La fonction var() restitue la matrice de variance-covariance d’une matrice ou d’un data-frame : | La fonction '''''var()''''' restitue la matrice de variance-covariance d’une matrice ou d’un data-frame : | ||
var(USArrests) | var(USArrests) | ||
| Ligne 447 : | Ligne 172 : | ||
=== Corrélation === | === Corrélation === | ||
La fonction cor() restitue la matrice de corrélation d’une matrice ou d’un data-frame : | La fonction '''''cor()''''' restitue la matrice de corrélation d’une matrice ou d’un data-frame : | ||
cor(USArrests) | cor(USArrests) | ||
=== Test sur un coefficient de corrélation === | === Test sur un coefficient de corrélation === | ||
La fonction t.test() permet de tester la significativité d’un coefficient de corrélation donnée : | La fonction '''''t.test()''''' permet de tester la significativité d’un coefficient de corrélation donnée : | ||
x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2, 60.1) | x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2, 60.1) | ||
y <- c( 2.6, 3.1, 2.5, 5.0, 3.6, 4.0, 5.2, 2.8, 3.8) | y <- c( 2.6, 3.1, 2.5, 5.0, 3.6, 4.0, 5.2, 2.8, 3.8) | ||
| Ligne 459 : | Ligne 184 : | ||
=== Régression linéaire simple === | === Régression linéaire simple === | ||
La fonction lm() permet de bâtir de modèles de régression linéaire simple : | La fonction '''''lm()''''' permet de bâtir de modèles de régression linéaire simple : | ||
plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") | plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") | ||
LinMod4 <- lm(USArrests$Murder~USArrests$Assault) | LinMod4 <- lm(USArrests$Murder~USArrests$Assault) | ||
| Ligne 472 : | Ligne 197 : | ||
=== Régression linéaire multiple === | === Régression linéaire multiple === | ||
La fonction lm() permet de bâtir de modèles de régression linéaire multiple | La fonction '''''lm()''''' permet de bâtir de modèles de régression linéaire multiple : | ||
data <- USArrests[,c(1,2,4)] | data <- USArrests[,c(1,2,4)] | ||
pairs(data) | pairs(data) | ||
| Ligne 479 : | Ligne 204 : | ||
anova(LinMod5) | anova(LinMod5) | ||
Un modèle linéaire nécessite la normalité des résidus et l'homoscédasticité. Utilisez le code suivant pour vérifier si ces deux conditions sont remplies : par(mfrow = c(2,2)) | Un modèle linéaire nécessite la normalité des résidus et l'homoscédasticité. Utilisez le code suivant pour vérifier si ces deux conditions sont remplies : | ||
par(mfrow = c(2,2)) | |||
plot(LinMod5, col.smooth = "black") # Analyse des résidus | plot(LinMod5, col.smooth = "black") # Analyse des résidus | ||
=== Analyse en | == Statistiques inférentielles : t-test, Analyse de variance == | ||
=== Test de T sur un échantillon unique === | |||
La fonction '''''t.test()''''' permet – entre d’autres – de comparer une moyenne observée à une moyenne théorique. | |||
Test bilatéral: | |||
notes <- c(4, 4, 4.5, 3, 5, 6, 5.5, 5, 4, 3.5, 3, 5.5, 4, 6, 5, 5.5) | |||
m.theo <- 4.5 | |||
t.test(notes, mu = m.theo) | |||
Test unilatéral droit: | |||
m.theo <- 4 | |||
t.test(notes, mu = m.theo, alternative = "greater") | |||
Test unilatéral gauche: | |||
m.theo <- 5 | |||
t.test(notes, mu = m.theo, alternative = "less") | |||
Ce test nécessite la normalité des données de l'échantillon. Vous pouvez la tester avec le code suivant ('''Attention!''' Le test de normalité de Shapiro-Wilk a pour hypothèse nulle que l'échantillon est normalement distribué! En résumé, si votre test est significatif, alors la distribution n'est pas normale) : | |||
shapiro.test(notes) | |||
=== Test de T sur deux échantillons indépendants avec variance égales === | |||
La fonction '''''t.test()''''' permet – entre d’autres – de comparer deux moyennes issues de deux échantillons indépendants avec variances égales. | |||
Test bilatéral: | |||
A <- c(3,4,5,4,3,4,4,4,5,3,3,6,1,2) | |||
B <- c(5,7,6,4,5,3,5,5,3,6,5,5,4,4,4,5,4) | |||
var.test(A,B) # Test sur la variance | |||
t.test(A, B, paired = FALSE, var.qual = TRUE) | |||
Test unilatéral droit: | |||
t.test(A, B, paired = FALSE, var.qual = TRUE, alternative = "greater") | |||
Test unilatéral gauche: | |||
t.test(A, B, paired = FALSE, var.qual = TRUE, alternative = "less") | |||
Ce test nécessite la normalité des données dans chaque sous-population. Vous pouvez la tester avec le code suivant ('''Attention!''' Le test de normalité de Shapiro-Wilk a pour hypothèse nulle que l'échantillon est normalement distribué! En résumé, si votre test est significatif, alors la distribution n'est pas normale) : | |||
shapiro.test(A) | |||
shapiro.test(B) | |||
=== Test de T sur deux échantillons indépendants avec variance différente === | |||
La fonction '''''t.test()''''' permet – entre d’autres – de comparer deux moyennes issues de deux échantillons indépendants avec variances différentes (Test de Welch). | |||
Test bilatéral: | |||
C <- c(2,4,5,4,2,3,5,4,6,4,2,7,1,2,1,3) | |||
D <- c(5,6,4,5,3,5,6,5,5,4,4,5,4) | |||
var.test(C,D) # Test sur la variance | |||
t.test(C, D, paired = FALSE, var.qual = FALSE) | |||
Test unilatéral droit: | |||
t.test(C, D, paired = FALSE, var.qual = FALSE, alternative = "greater") | |||
Test unilatéral gauche: | |||
t.test(C, D, paired = FALSE, var.qual = FALSE, alternative = "less") | |||
Ce test nécessite la normalité des données dans chaque sous-population. Vous pouvez la tester avec le code suivant : | |||
shapiro.test(C) | |||
shapiro.test(D) | |||
=== Test de T sur deux échantillons dépendants === | |||
La fonction '''''t.test()''''' permet – entre d’autres – de comparer deux moyennes issues de deux échantillons dépendants. | |||
Test bilatéral: | |||
E <- c(3,4,5,4,3,4,4,4,5,3,3,6,1,2) | |||
F <- c(5,7,6,4,5,3,5,5,3,6,5,5,4,4) | |||
t.test(E, F, paired = TRUE) | |||
Test unilatéral droit: | |||
t.test(E, F, paired = TRUE, alternative = "greater") | |||
Test unilatéral gauche: | |||
t.test(E, F, paired = TRUE, alternative = "less") | |||
Ce test nécessite la normalité dans les scores des différences: | |||
shapiro.test(F-E) | |||
=== ANOVA à un critère de classification === | |||
La fonction '''''lm()''''' permet de créer des modèles linéaires. De ce fait, elle peut être utilisée pour construire des modèles ANOVA. | |||
data(InsectSprays) | |||
boxplot(InsectSprays$count ~ InsectSprays$spray) | |||
LinMod1 <-lm(InsectSprays$count ~ InsectSprays$spray) | |||
summary(LinMod1) # Paramètres du modèle | |||
anova(LinMod1) # Tableau de l’ANOVA | |||
Condition d’application : normalité des résidus et homoscédasticité | |||
par(mfrow = c(2,2)) | |||
plot(LinMod1, col.smooth = "black") # Analyse des résidus | |||
bartlett.test(InsectSprays$count ~ InsectSprays$spray) # Test sur l’homogénéité des variance de Bartlett | |||
library(car) | |||
leveneTest(InsectSprays$count ~ InsectSprays$spray) # Test sur l’homogénéité des variance de Levene. Pour utiliser cette fonction il faut installer le package « car ». | |||
=== ANOVA à deux critères de classification === | |||
La fonction '''''lm()''''' permet de créer des modèles linéaires. De ce fait, elle peut être utilisée pour construire des modèles ANOVA : | |||
data(CO2) | |||
boxplot(CO2$uptake ~ CO2$Treatment * CO2$Type) | |||
interaction.plot(CO2$Treatment, CO2$Type, CO2$uptake, main = "Graphique des moyennes", xlab = "Traitement", ylab = "Consommation de CO2", trace.label = "Provenance") | |||
Modèle avec interaction (multiplicatif) : | |||
LinMod2 <- lm(CO2$uptake ~ CO2$Treatment * CO2$Type) # Construction du modèle avec interaction (multiplicatif) | |||
summary(LinMod2) # Paramètres du modèle | |||
anova(LinMod2) # Tableau de l’ANOVA | |||
Condition d’application : normalité des résidus et homoscédasticité | |||
par(mfrow = c(2,2)) | |||
plot(LinMod2, col.smooth = "black") # Analyse des résidus | |||
bartlett.test(CO2$uptake ~ CO2$Treatment * CO2$Type) # Test sur l’homogénéité des variance de Bartlett | |||
library(car) | |||
leveneTest(CO2$uptake ~ CO2$Treatment * CO2$Type) # Test sur l’homogénéité des variance de Levene. Pour utiliser cette fonction il faut installer le package « car ». | |||
== Graphes et réseaux == | |||
Il y a deux packages sur R permettant de générer et analyser des réseaux : [http://igraph.sourceforge.net/ igraph] et [http://statnet.org/ statnet]. Ces deux outils présentent des avantages et des désavantages : | |||
* [http://igraph.sourceforge.net/ igraph] permet de représenter les réseaux de manière efficace et élégante. De plus, il s’agit d’un outil intéressant pour génération aléatoire des graphes (simulation). Pour une utilisation de [http://igraph.sourceforge.net/ igraph], vous pouvez consulter la page | |||
** {{ Goblock | [[Analyse de réseaux avec R]] }} | |||
* Contrairement à [http://igraph.sourceforge.net/ igraph], [http://statnet.org/ statnet] permet de faire de la modélisation statistique (voir Exponential random graph models – ERGP). | |||
Nous nous limiterons ici à présenter [http://statnet.org/ statnet]. | |||
=== Générer un graphe === | |||
Pour créer un graphe, il faut avant tout créer une matrice d’adjacence ou une matrice des arrêts. Générons une matrice d’adjacence avec le code suivant : | |||
mat_adjacence <- matrix(round(runif(2500, max = 0.51)), ncol = 50) | |||
La matrice des arêtes peut être crée de la manière suivante : | |||
depart <- c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'C', 'C', 'D', 'D', 'D', 'D', 'D', 'F', 'G', 'G') | |||
arrive <- c('B', 'C', 'D', 'F', 'G', 'A', 'C', 'G', 'F', 'G', 'A', 'B', 'C', 'F', 'G', 'H', 'B', 'C') | |||
mat_aretes <- cbind(depart,arrive) | |||
La fonction '''''as.network()''''' permet de transformer une matrice d’adjacence ou une matrice des arrêts en un objet de type network (un graphe). Pour utiliser cette fonction, il faut charger la librarie statnet : | |||
library(statnet) | |||
G1 <- as.network(mat_adjacence) | |||
G2 <- as.network(mat_aretes) | |||
Alternativement, nous pouvons générer un graphe aléatoire en définissant le nombre de sommets et sa densité : | |||
G3 <- rgraph(20, tprob = 0.1) # G3 est un graphe aléatoire de 20 sommets, avec densité 0.1 | |||
=== Représenter un graphe === | |||
Les fonctions gplot et gplot3d permettent de générer des graphiques en 2 et 3 dimensions : | |||
gplot(G1) | |||
gplot3d(G1) | |||
gplot(G2) | |||
gplot3d(G2) | |||
gplot(G3) | |||
gplot3d(G3) | |||
La fonction '''''plot.sociomatrix()''''' permet de représenter de manière efficace la matrice d'adjacence d'un graphe : | |||
plot.sociomatrix(G2) | |||
=== Indices, indicateurs === | |||
La librairie statnet permet de calculer des indicateurs permettant de décrire les réseaux et leurs éléments. | |||
==== Au niveau du réseau ==== | |||
La fonction gden permet d’obtenir la densité d’un reseau : | |||
gden(G1) | |||
gden(G2) | |||
gden(G3) | |||
La fonction '''''grecip()''''' permet de calculer le degré de réciprocité d'un réseau : | |||
grecip(G1) | |||
grecip(G2) | |||
grecip(G3) | |||
La fonction '''''gtrans()''''' permet d’estimer le niveau de transitivité d’un graphe donné : | |||
gtrans(G1) | |||
gtrans(G2) | |||
gtrans(G3) | |||
La fonction connectedness d’éstimer le degré de connexité d’un réseau : | |||
connectedness(G1) | |||
connectedness(G2) | |||
connectedness(G3) | |||
==== Au niveau des sommets ==== | |||
La fonction '''''degree()''''' permet d’obtenir le degré de chaque sommet du graphe. L’argument cmode permet de spécifier si on s’intéresse aux degrés entrants (indegree), sortants (outdegree), ou totaux (freeman) : | |||
degree(G1, cmode = "indegree") | |||
degree(G1, cmode = "outdegree") | |||
degree(G1, cmode = "freeman") | |||
degree(G2, cmode = "indegree") | |||
degree(G2, cmode = "outdegree") | |||
degree(G2, cmode = "freeman") | |||
degree(G3, cmode = "indegree") | |||
degree(G3, cmode = "outdegree") | |||
degree(G3, cmode = "freeman") | |||
Lorsqu’on étude un réseau comportant un grand nombre de sommets, on peut étudier le tri à plat des degrés : | |||
table(degree(G1, cmode = "indegree")) | |||
table(degree(G1, cmode = "outdegree")) | |||
table(degree(G1, cmode = "freeman")) | |||
La centralité de proximité peut être mesurée à partir de la fonction '''''closeness()''''' : | |||
closeness(G1) | |||
closeness(G2) | |||
closeness(G3) | |||
La fonction '''''betweenness()''''' permet d’obtenir la centralité d’intermédiarité : | |||
betweenness(G1) | |||
betweenness(G2) | |||
betweenness(G3) | |||
'''''infocent()''''' permet d’évaluer le niveau de centralité de chaque sommet vis-à-vis de la circulation de l’information : | |||
infocent(G1) | |||
infocent(G2) | |||
infocent(G3) | |||
Les indices de '''''closeness(), de betweenness(), infocent()''''' peuvent être représentées sur la représentation du réseau : | |||
gplot(G2, vertex.cex = closeness (G2) * 3, main = " closeness ") | |||
gplot(G2, vertex.cex = betweenness(G2) * 0.6, main = "betweenness") | |||
gplot(G2, vertex.cex = infocent (G2) * 1.3, main = " infocent ") | |||
La fonction '''''geodist()$count''''' permet de compter le nombre de chemins possibles entre chaque paire de sommets du réseau : | |||
geodist(G2)$count | |||
La fonction '''''geodist()$gdist''''' indique la distance entre chaque paire de sommets du sommet. La distance se définie par la longueur d’un plus court chemin. | |||
geodist(G2)$gdist | |||
=== Analyse de réseaux === | |||
* {{ Goblock | [[Analyse de réseaux avec R]] }} | |||
== Liens == | |||
== | === Packages utiles pour l'analyse statistique === | ||
* Rcmdr : interface graphique de R , http://socserv.mcmaster.ca/jfox/Misc/Rcmdr/ | |||
* OpenMx : outil permettant de générer et évaluer des modèles à équations structurales , http://openmx.psyc.virginia.edu/ | |||
* igraph : outil permettant de créer et analyser des graphes et des réseaux , http://igraph.sourceforge.net/ | |||
* statnet : outil permettant de créer et analyser des graphes et des réseaux , http://statnet.csde.washington.edu/ | |||
* lattice : outil permettant de générer des représentations graphiques avancées , http://lmdvr.r-forge.r-project.org/figures/figures.html | |||
* R.matlab : outil permettant d’importer des fichiers Matlab sur R , http://cran.r-project.org/web/packages/R.matlab/R.matlab.pdf | |||
* R2HTML : outil permettant d'exporter les outputs de R en HTML , http://cran.r-project.org/web/packages/R2HTML/R2HTML.pdf | |||
* corrgram : outil permettant de représenter graphiquement des matrices de corrélations , http://cran.r-project.org/web/packages/corrgram/corrgram.pdf | |||
* 3dscatterplot : outil permettant à créer des graphiques 3D , http://cran.r-project.org/web/packages/scatterplot3d/scatterplot3d.pdf | |||
* [http://lavaan.ugent.be/lavaan lavaan]: latent variable analysis | |||
* [http://sachaepskamp.com/semPlot semPlot]: outil pour visualiser des modèles SEM, http://cran.r-project.org/web/packages/semPlot/index.html | |||
= | === Autres tutoriels === | ||
* [http://www.unige.ch/ses/sococ/cl/r/toc.html Tutoriels R de E.Horber] (UniGE) | |||
* [http://www.statmethods.net/ Statmethods.net] (Quick-R) | |||
[[Utilisateur:Cereghd0|Cereghd0]] 9 janvier 2013 à 12:27 (CET) | |||
[[Category: Analytique et exploration de données]] | |||
[[Category: R]] | |||
Dernière version du 7 décembre 2022 à 12:13
| Tutoriels R | |
|---|---|
| Module: Tutoriels R | |
| ◀▬ | |
| ⚐ à finaliser | ☸ |
| ⚒ 2022/12/07 | |
| Voir aussi | |
| Catégorie: Tutoriels R | |
Introduction
Cet article fournit un tutoriel conçis sur le traitement des données numériques avec R. Une explication plus conceptuelle sur le fonctionnement de R pour les analyses est disponible dans la page Introduction à la modélisation des données avec R.
Les opérateurs arithmétiques classiques
La somme : +
3+5
La soustraction : -
5-1
La multiplication : *
3*2
La division : /
8/2
L’exposant : ^
3^3
La racine carrée : sqrt()
sqrt(9)
Le modulo (donne le reste d’une division) : %%
10%%3
Représenter des données sur R
L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : hist(), density(), lines(), boxplot(), barplot(), pie(),mosaicplot(), assocplot(), plot(), abline(), pairs(), scatterplot3d().
Histogramme et fonction de densité
L’histogramme permet de représenter la distribution d’une variable continue. Vous pouvez construire des histogrammes avec la fonction hist() :
data(iris) hist(iris$Sepal.Length, prob = FALSE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Effectif ", col = "lightblue") # Histogramme en effectif hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité
La fonction density() permet d’obtenir un estimateur à noyau de la densité :
plot(density(iris$Sepal.Length))
Pour tracer l'histogramme et la densité en même temps on peut utiliser le code suivant :
hist(iris$Sepal.Length, prob = TRUE, main = "Histogramme de la longueur des sépales", xlab = "Longueur des sépales", ylab = "Densité de la distribution", col = "lightblue") # Histogramme en densité lines(density(iris$Sepal.Length),col="red")
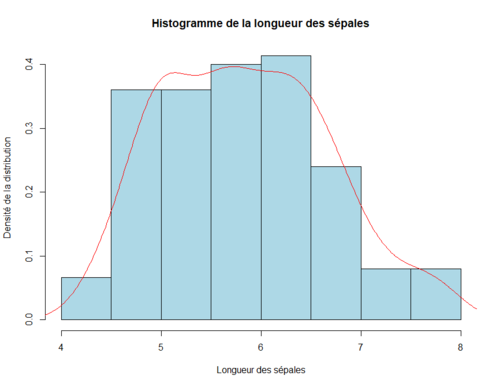
Boite à moustache
La boîte à moustache est une méthode rapide pour représenter et résumer le profil d’une variable continue. Pour créer une boîte à moustache utilisez la fonction boxplot() :
A <- rnorm(1000, 100, 10) # A est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 100 et d'écart-type 10
B <- rnorm(1000, 120, 20) # B est un vecteur de 1000 valeurs tirées d'une distribution gaussienne de moyenne 120 et d'écart-type 20
boxplot(A, main = "Distribution des valeurs générés")
boxplot(list(A, B), main = "Distribution des valeurs générés" , names = c("µ = 100, sd = 10", "µ = 120, sd = 20 "))
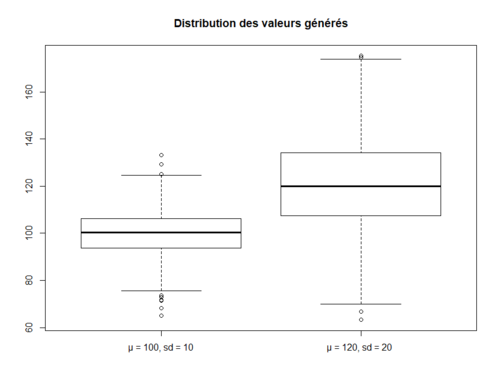
Diagramme en tuyaux d’orgue
Le diagramme en tuyaux d’orgue permet de représenter graphiquement la distribution d'une variable discrète. Pour créer un diagramme en tuyaux d’orgue, utilisez la fonction barplot() :
ventes <- c(200, 102, 32, 120, 310, 152)
names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon")
barplot(ventes, main = "Diagramme des ventes", col = "lightblue")
barplot(ventes, main = "Diagramme des ventes", col = "lightblue", horiz = TRUE)
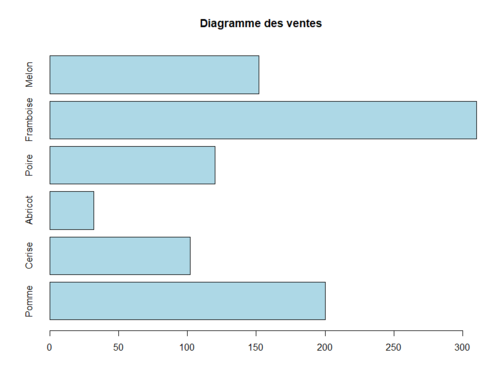
Diagramme circulaire
Le diagramme circulaire permet de représenter des variables discrètes. Utilisez la fonction pie() pour construire des diagrammes circulaires :
ventes <- c(200, 102, 32, 120, 310, 152)
names(ventes) <- c("Pomme","Cerise", "Abricot", "Poire", "Framboise", "Melon")
pie(ventes, main = "Diagramme des ventes", col = rainbow(length(ventes)))
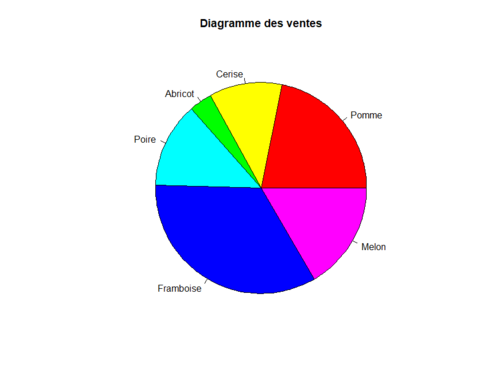
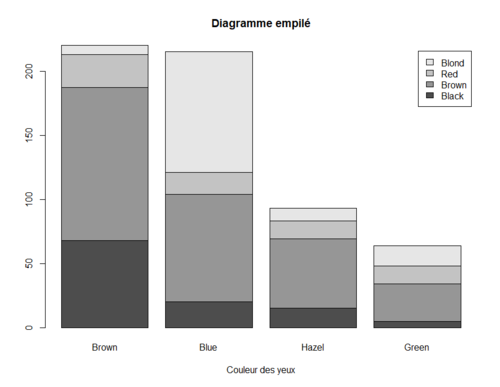
Diagramme empilé
Le diagramme empilé permet de représenter graphiquement les effectifs d’un tableau de contingence. Le diagramme empilé s’obtient au moyen de la fonction barplot() en fournissant un objet de mode matrix :
data(HairEyeColor) HairEye <- apply(HairEyeColor, c(1, 2), sum) barplot(HairEye, legend = rownames(HairEye), main = "Diagramme empilé", xlab = "Couleur des yeux")
Diagrammes en mosaïque
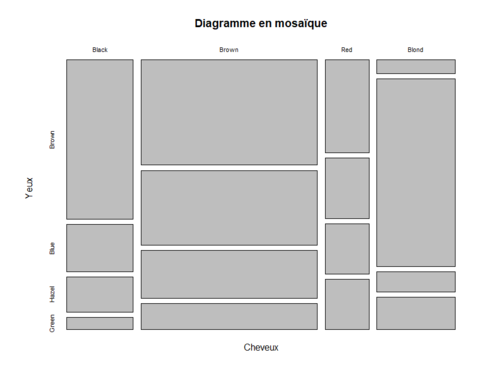
Le diagramme en mosaïque permet de représenter graphiquement les effectifs d’un tableau de contingence. De ce fait, la surface des mosaïques est proportionnelle aux effectifs observés dans les cellules du tableau de contingence. Pour créer un diagramme en mosaïque utilisez la fonction mosaicplot() :
mosaicplot(HairEye, main = "Diagramme en mosaïque", xlab = "Cheveux", ylab = "Yeux")
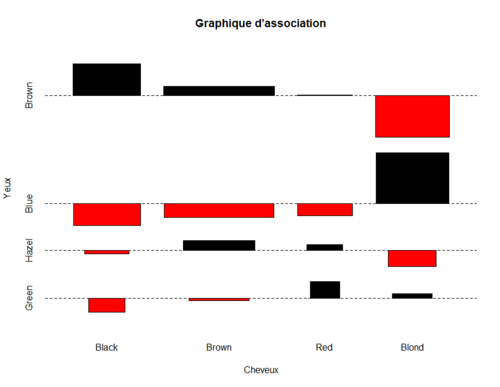
Graphique d’association
Le graphique d’association de Cohen-Friendly indique les déviations par rapport à l’indépendance dans une table de contingence. Utilisez la fonction assocplot() pour créer un graphique d’association :
assocplot(HairEye, main = "Graphique d’association", xlab = "Cheveux", ylab = "Yeux")
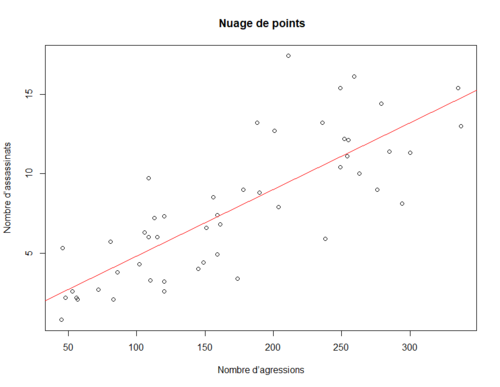
Nuage des points 2D
La fonction plot() permet – entre d’autres – de représenter deux variables continues dans un plan cartésien. Exemple :
data(USArrests) plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") abline(lm(USArrests$Murder~USArrests$Assault), col = "red")
Remarque : la fonction “lm” permet de créer des modèles linéaires (on y reviendra).
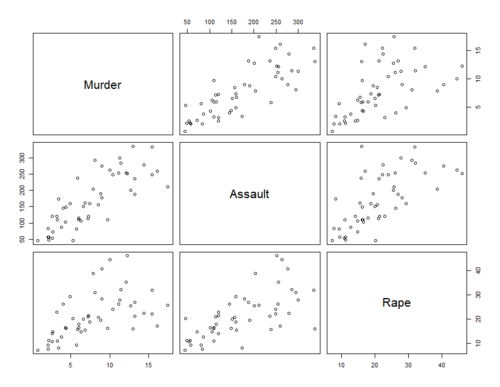
Matrice des scatter plots
La fonction pairs() permet de représenter un scatter plot pour chaque couple possible de colonnes d’un dataframe ou d’une matrice donnée :
data <- USArrests[,c(1,2,4)] pairs(data)
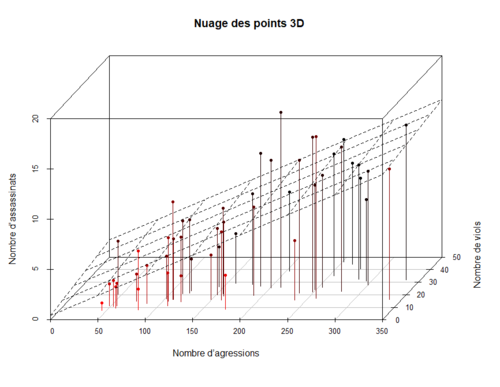
Nuage des points 3D
La fonction scatterplot3d() permet de représenter trois variables dans un espace tridimensionnel. Pour utiliser cette fonction il faut installer le package « scatterplot3d » :
library(scatterplot3d) s3d <- scatterplot3d(USArrests$Assault, USArrests$Rape, USArrests$Murder, type= "h", highlight.3d = TRUE, angle = 45, scale.y = 0.5, pch = 20, main = "Nuage des points 3D", xlab = "Nombre d’agressions", ylab = " Nombre de viols", zlab = "Nombre d’assassinats") s3d$plane3d(lm(USArrests$Murder ~ USArrests$Assault + USArrests$Rape))
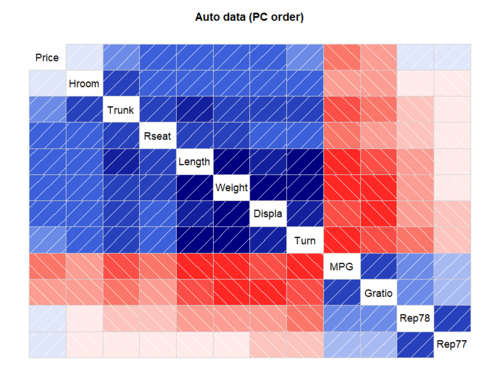
Corrgram
La fonction corrgram() permet de représenter graphiquement une matrice de corrélation de manière efficace. Pour utiliser cette fonction il faut installer le package « corrgram » :
library(corrgram) data(auto) corrgram(auto, order=TRUE, main="Auto data (PC order)")
Traitements statistiques élémentaires
L’objectif de ce chapitre est d’apprendre à utiliser les fonctions : mean(), sd(), median(), quantile(), min(), max(), summary() et cov().
Mesures de tendance centrale, de dispersion et de position
Les fonctions mean(), sd() restituent la moyenne, et respectivement l’écart-type d’un objet donné :
mean(USArrests$Murder) sd(USArrests$Murder)
Les fonctions median() et quantile() restituent le médian et les quantiles désirées :
median(USArrests$Murder) quantile(USArrests$Murder, c(0.25, 0.5, 0.75)) # Donne les 3 quartiles quantile(USArrests$Murder, c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9)) # Donne les 9 déciles
Les fonctions min() et max() restituent la valeur minimale et maximale d’un objet :
min(USArrests$Murder) max(USArrests$Murder)
Résumé statistique
La fonction summary() fournit une série d’information qui varie en fonction de l’objet d’input :
summary(iris) summary(USArrests)
Matrice de variance-covariance
La fonction var() restitue la matrice de variance-covariance d’une matrice ou d’un data-frame :
var(USArrests)
Approches corrélationnels
Corrélation
La fonction cor() restitue la matrice de corrélation d’une matrice ou d’un data-frame :
cor(USArrests)
Test sur un coefficient de corrélation
La fonction t.test() permet de tester la significativité d’un coefficient de corrélation donnée :
x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2, 60.1) y <- c( 2.6, 3.1, 2.5, 5.0, 3.6, 4.0, 5.2, 2.8, 3.8) cor.test(x,y)
Régression linéaire simple
La fonction lm() permet de bâtir de modèles de régression linéaire simple :
plot(USArrests$Murder~USArrests$Assault, main = " Nuage de points", xlab = "Nombre d’agressions", ylab = "Nombre d’assassinats") LinMod4 <- lm(USArrests$Murder~USArrests$Assault) summary(LinMod4) # Paramètres du modèle anova(LinMod4) abline(LinMod4, col= "red")
Un modèle linéaire nécessite la normalité des résidus et l'homoscédasticité. Utilisez le code suivant pour vérifier si ces deux conditions sont remplies :
par(mfrow = c(2,2)) plot(LinMod4, col.smooth = "black") # Analyse des résidus
Régression linéaire multiple
La fonction lm() permet de bâtir de modèles de régression linéaire multiple :
data <- USArrests[,c(1,2,4)] pairs(data) LinMod5 <- lm(USArrests$Murder ~ USArrests$Assault + USArrests$Rape) summary(LinMod5) # Paramètres du modèle anova(LinMod5)
Un modèle linéaire nécessite la normalité des résidus et l'homoscédasticité. Utilisez le code suivant pour vérifier si ces deux conditions sont remplies :
par(mfrow = c(2,2)) plot(LinMod5, col.smooth = "black") # Analyse des résidus
Statistiques inférentielles : t-test, Analyse de variance
Test de T sur un échantillon unique
La fonction t.test() permet – entre d’autres – de comparer une moyenne observée à une moyenne théorique.
Test bilatéral:
notes <- c(4, 4, 4.5, 3, 5, 6, 5.5, 5, 4, 3.5, 3, 5.5, 4, 6, 5, 5.5) m.theo <- 4.5 t.test(notes, mu = m.theo)
Test unilatéral droit:
m.theo <- 4 t.test(notes, mu = m.theo, alternative = "greater")
Test unilatéral gauche:
m.theo <- 5 t.test(notes, mu = m.theo, alternative = "less")
Ce test nécessite la normalité des données de l'échantillon. Vous pouvez la tester avec le code suivant (Attention! Le test de normalité de Shapiro-Wilk a pour hypothèse nulle que l'échantillon est normalement distribué! En résumé, si votre test est significatif, alors la distribution n'est pas normale) :
shapiro.test(notes)
Test de T sur deux échantillons indépendants avec variance égales
La fonction t.test() permet – entre d’autres – de comparer deux moyennes issues de deux échantillons indépendants avec variances égales.
Test bilatéral:
A <- c(3,4,5,4,3,4,4,4,5,3,3,6,1,2) B <- c(5,7,6,4,5,3,5,5,3,6,5,5,4,4,4,5,4) var.test(A,B) # Test sur la variance t.test(A, B, paired = FALSE, var.qual = TRUE)
Test unilatéral droit:
t.test(A, B, paired = FALSE, var.qual = TRUE, alternative = "greater")
Test unilatéral gauche:
t.test(A, B, paired = FALSE, var.qual = TRUE, alternative = "less")
Ce test nécessite la normalité des données dans chaque sous-population. Vous pouvez la tester avec le code suivant (Attention! Le test de normalité de Shapiro-Wilk a pour hypothèse nulle que l'échantillon est normalement distribué! En résumé, si votre test est significatif, alors la distribution n'est pas normale) :
shapiro.test(A) shapiro.test(B)
Test de T sur deux échantillons indépendants avec variance différente
La fonction t.test() permet – entre d’autres – de comparer deux moyennes issues de deux échantillons indépendants avec variances différentes (Test de Welch).
Test bilatéral:
C <- c(2,4,5,4,2,3,5,4,6,4,2,7,1,2,1,3) D <- c(5,6,4,5,3,5,6,5,5,4,4,5,4) var.test(C,D) # Test sur la variance t.test(C, D, paired = FALSE, var.qual = FALSE)
Test unilatéral droit:
t.test(C, D, paired = FALSE, var.qual = FALSE, alternative = "greater")
Test unilatéral gauche:
t.test(C, D, paired = FALSE, var.qual = FALSE, alternative = "less")
Ce test nécessite la normalité des données dans chaque sous-population. Vous pouvez la tester avec le code suivant :
shapiro.test(C) shapiro.test(D)
Test de T sur deux échantillons dépendants
La fonction t.test() permet – entre d’autres – de comparer deux moyennes issues de deux échantillons dépendants.
Test bilatéral:
E <- c(3,4,5,4,3,4,4,4,5,3,3,6,1,2) F <- c(5,7,6,4,5,3,5,5,3,6,5,5,4,4) t.test(E, F, paired = TRUE)
Test unilatéral droit:
t.test(E, F, paired = TRUE, alternative = "greater")
Test unilatéral gauche:
t.test(E, F, paired = TRUE, alternative = "less")
Ce test nécessite la normalité dans les scores des différences:
shapiro.test(F-E)
ANOVA à un critère de classification
La fonction lm() permet de créer des modèles linéaires. De ce fait, elle peut être utilisée pour construire des modèles ANOVA.
data(InsectSprays) boxplot(InsectSprays$count ~ InsectSprays$spray) LinMod1 <-lm(InsectSprays$count ~ InsectSprays$spray) summary(LinMod1) # Paramètres du modèle anova(LinMod1) # Tableau de l’ANOVA
Condition d’application : normalité des résidus et homoscédasticité
par(mfrow = c(2,2)) plot(LinMod1, col.smooth = "black") # Analyse des résidus bartlett.test(InsectSprays$count ~ InsectSprays$spray) # Test sur l’homogénéité des variance de Bartlett library(car) leveneTest(InsectSprays$count ~ InsectSprays$spray) # Test sur l’homogénéité des variance de Levene. Pour utiliser cette fonction il faut installer le package « car ».
ANOVA à deux critères de classification
La fonction lm() permet de créer des modèles linéaires. De ce fait, elle peut être utilisée pour construire des modèles ANOVA :
data(CO2) boxplot(CO2$uptake ~ CO2$Treatment * CO2$Type) interaction.plot(CO2$Treatment, CO2$Type, CO2$uptake, main = "Graphique des moyennes", xlab = "Traitement", ylab = "Consommation de CO2", trace.label = "Provenance")
Modèle avec interaction (multiplicatif) :
LinMod2 <- lm(CO2$uptake ~ CO2$Treatment * CO2$Type) # Construction du modèle avec interaction (multiplicatif) summary(LinMod2) # Paramètres du modèle anova(LinMod2) # Tableau de l’ANOVA
Condition d’application : normalité des résidus et homoscédasticité
par(mfrow = c(2,2)) plot(LinMod2, col.smooth = "black") # Analyse des résidus bartlett.test(CO2$uptake ~ CO2$Treatment * CO2$Type) # Test sur l’homogénéité des variance de Bartlett library(car) leveneTest(CO2$uptake ~ CO2$Treatment * CO2$Type) # Test sur l’homogénéité des variance de Levene. Pour utiliser cette fonction il faut installer le package « car ».
Graphes et réseaux
Il y a deux packages sur R permettant de générer et analyser des réseaux : igraph et statnet. Ces deux outils présentent des avantages et des désavantages :
- igraph permet de représenter les réseaux de manière efficace et élégante. De plus, il s’agit d’un outil intéressant pour génération aléatoire des graphes (simulation). Pour une utilisation de igraph, vous pouvez consulter la page
- Contrairement à igraph, statnet permet de faire de la modélisation statistique (voir Exponential random graph models – ERGP).
Nous nous limiterons ici à présenter statnet.
Générer un graphe
Pour créer un graphe, il faut avant tout créer une matrice d’adjacence ou une matrice des arrêts. Générons une matrice d’adjacence avec le code suivant :
mat_adjacence <- matrix(round(runif(2500, max = 0.51)), ncol = 50)
La matrice des arêtes peut être crée de la manière suivante :
depart <- c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'C', 'C', 'D', 'D', 'D', 'D', 'D', 'F', 'G', 'G')
arrive <- c('B', 'C', 'D', 'F', 'G', 'A', 'C', 'G', 'F', 'G', 'A', 'B', 'C', 'F', 'G', 'H', 'B', 'C')
mat_aretes <- cbind(depart,arrive)
La fonction as.network() permet de transformer une matrice d’adjacence ou une matrice des arrêts en un objet de type network (un graphe). Pour utiliser cette fonction, il faut charger la librarie statnet :
library(statnet) G1 <- as.network(mat_adjacence) G2 <- as.network(mat_aretes)
Alternativement, nous pouvons générer un graphe aléatoire en définissant le nombre de sommets et sa densité :
G3 <- rgraph(20, tprob = 0.1) # G3 est un graphe aléatoire de 20 sommets, avec densité 0.1
Représenter un graphe
Les fonctions gplot et gplot3d permettent de générer des graphiques en 2 et 3 dimensions :
gplot(G1) gplot3d(G1) gplot(G2) gplot3d(G2) gplot(G3) gplot3d(G3)
La fonction plot.sociomatrix() permet de représenter de manière efficace la matrice d'adjacence d'un graphe :
plot.sociomatrix(G2)
Indices, indicateurs
La librairie statnet permet de calculer des indicateurs permettant de décrire les réseaux et leurs éléments.
Au niveau du réseau
La fonction gden permet d’obtenir la densité d’un reseau :
gden(G1) gden(G2) gden(G3)
La fonction grecip() permet de calculer le degré de réciprocité d'un réseau :
grecip(G1) grecip(G2) grecip(G3)
La fonction gtrans() permet d’estimer le niveau de transitivité d’un graphe donné :
gtrans(G1) gtrans(G2) gtrans(G3)
La fonction connectedness d’éstimer le degré de connexité d’un réseau :
connectedness(G1) connectedness(G2) connectedness(G3)
Au niveau des sommets
La fonction degree() permet d’obtenir le degré de chaque sommet du graphe. L’argument cmode permet de spécifier si on s’intéresse aux degrés entrants (indegree), sortants (outdegree), ou totaux (freeman) :
degree(G1, cmode = "indegree") degree(G1, cmode = "outdegree") degree(G1, cmode = "freeman")
degree(G2, cmode = "indegree") degree(G2, cmode = "outdegree") degree(G2, cmode = "freeman")
degree(G3, cmode = "indegree") degree(G3, cmode = "outdegree") degree(G3, cmode = "freeman")
Lorsqu’on étude un réseau comportant un grand nombre de sommets, on peut étudier le tri à plat des degrés :
table(degree(G1, cmode = "indegree")) table(degree(G1, cmode = "outdegree")) table(degree(G1, cmode = "freeman"))
La centralité de proximité peut être mesurée à partir de la fonction closeness() :
closeness(G1) closeness(G2) closeness(G3)
La fonction betweenness() permet d’obtenir la centralité d’intermédiarité :
betweenness(G1) betweenness(G2) betweenness(G3)
infocent() permet d’évaluer le niveau de centralité de chaque sommet vis-à-vis de la circulation de l’information :
infocent(G1) infocent(G2) infocent(G3)
Les indices de closeness(), de betweenness(), infocent() peuvent être représentées sur la représentation du réseau :
gplot(G2, vertex.cex = closeness (G2) * 3, main = " closeness ") gplot(G2, vertex.cex = betweenness(G2) * 0.6, main = "betweenness") gplot(G2, vertex.cex = infocent (G2) * 1.3, main = " infocent ")
La fonction geodist()$count permet de compter le nombre de chemins possibles entre chaque paire de sommets du réseau :
geodist(G2)$count
La fonction geodist()$gdist indique la distance entre chaque paire de sommets du sommet. La distance se définie par la longueur d’un plus court chemin.
geodist(G2)$gdist
Analyse de réseaux
Liens
Packages utiles pour l'analyse statistique
- Rcmdr : interface graphique de R , http://socserv.mcmaster.ca/jfox/Misc/Rcmdr/
- OpenMx : outil permettant de générer et évaluer des modèles à équations structurales , http://openmx.psyc.virginia.edu/
- igraph : outil permettant de créer et analyser des graphes et des réseaux , http://igraph.sourceforge.net/
- statnet : outil permettant de créer et analyser des graphes et des réseaux , http://statnet.csde.washington.edu/
- lattice : outil permettant de générer des représentations graphiques avancées , http://lmdvr.r-forge.r-project.org/figures/figures.html
- R.matlab : outil permettant d’importer des fichiers Matlab sur R , http://cran.r-project.org/web/packages/R.matlab/R.matlab.pdf
- R2HTML : outil permettant d'exporter les outputs de R en HTML , http://cran.r-project.org/web/packages/R2HTML/R2HTML.pdf
- corrgram : outil permettant de représenter graphiquement des matrices de corrélations , http://cran.r-project.org/web/packages/corrgram/corrgram.pdf
- 3dscatterplot : outil permettant à créer des graphiques 3D , http://cran.r-project.org/web/packages/scatterplot3d/scatterplot3d.pdf
- lavaan: latent variable analysis
- semPlot: outil pour visualiser des modèles SEM, http://cran.r-project.org/web/packages/semPlot/index.html
Autres tutoriels
- Tutoriels R de E.Horber (UniGE)
- Statmethods.net (Quick-R)
Cereghd0 9 janvier 2013 à 12:27 (CET)