Sens spatial

Le sens spatial

De la visualisation spatiale à la représentation spatiale le pas est encore très grand. Effectivement, même si Berthelot et Salin indiquait . « il suffit d’observer pour comprendre et de voir pour savoir » , l’application de cette conception, notamment dans le domaine des mathématiques reste complexe.(Berthelot & Salin, 1999).

Nombreuses études soulignent effectivement les difficultés que rencontrent les élèves face aux activités qui font appel aux connaissances spatiales (Bessot, 1994 ; Izard, 1990 ; Parzysz, 1991).

Dans un premier temps, il convient de déterminer ce qu’est le sens spatial, ensuite nous décrirons quelques modèles du sens spatial, ce qui nous permettra de comprendre son importance plus particulièrement dans le domaine des mathématiques.

Sens spatial et géométrie

Le sens spatial se réfère à tout ce qui est en lien avec la structuration d’un espace, plus spécifiquement ce qui permet de se situer, de s’orienter, de se déplacer dans son environnement; mais également ce qui amène l’élève à contrôler, anticiper et communiquer les états, les transformations ou les déformations des données d’objets relatifs à l’espace en 2D ou 3D. (Marchand, 2009)

Nombreuses activités permettent de vérifier les connaissances spatiales chez les élèves. Ce que Berthelot et Salin (Berthelot & Salin, 1999) ont constaté en contrôlant si des élèves savaient:

• reconnaître, décrire, fabriquer ou transformer des objets
• déplacer, trouver, communiquer la position d’objets
• reconnaitre, décrire, construire ou transformer un espace de vie ou de déplacement.

Des contrôles de connaissances spatiales se traduisant par des taches telles que les suivantes :

• Peux-tu m´ecrire un trajet me permettant de me rendre de la porte au tableau ?
• Peux-tu reproduire le Tangram que je te presente ?

Taches très proches de celles qui font appel aux connaissances géométriques, tel que les décrivent Clements et Battista (Clements & Battista, 1992). :

• Peux-tu me donner la définition d’un carré ?
• Est-ce qu’un carré est un rectangle ?
• Quel est le nom de ce solide ?

De ce fait on constate que connaissances spatiales et géométriques sont à la fois différentes mais pourtant très proches et surtout complémentaires pour les élèves dans leur apprentissage .

Modèles de développement des connaissances spatiales

Plusieurs modèles de développement des connaissances spatiales ont aiinsi été décrits. Parmi lesquels celui de van Hiele (Van Hiele, 1959), de Hoffer (1977), et de Marchand (Marchand, 2009).

Modèle de van Hiele

Van Hiele (Van Hiele, 1959) propose de classer les connaissances selon 5 niveaux :

• 1- Visuel (repères des dessins par ressemblance visuelle)
• 2- Analyse des propriétés (propriétés connues mais non reliées ensemble)
• 3- Ordre et hiérarchie (propriétés mises en relation et classées)
• 4-déduction et preuve
• 5-rigueur (déductions formelles et manipulations des symboles)

Orienté sur le langage et le développement axiomatique, ce modèle dont les niveaux sont jugés non suffisamment définis, est critiqué.

Modèle de Hoffer

Hoffer (Hoffer, 1977) présente un modèle sur la perception visuelle à sept composantes:

• La coordination visuo-motrice
• la perception image-fond
• la constance perceptuelle
• la perception de la position dans l'espace
• la perception des relations spatiales
• la distinction visuelle
• la mémoire visuelle

Ces sept composants sont également nommés habiletés visuo-spatiales. Ils forment à eux sept, le sens spatial. C

Modèle de Marchand

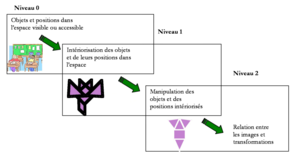
Plus récemment, selon Marchand (2009),l'apprentissage des connaissances spatiales se déroule selon trois niveaux que l'élève doit acquérir:

Marchand, 2009

• Niveau 0 : Il s'agit de manipulations et transformations concrète par l'élève de figures ou d'objets.
• Niveau 1 : Il s'agit là de la manipulation mentales des figures et solides par l'élève, suite à des transformations telles que rotation, symétrie, homothétie, translation...
• Niveau 2 : A ce stade, l'élève doit arriver à transformer mentalement figures et solides (par exemple, visualiser un cube dont on a coupé un coin à 45 degrés).

Selon la littérature, l'atteinte du niveau 2 s'effectue généralement chez les élèves du premier cycle du secondaire.

Ces 3 modèles bien que hiérarchique ne signifient pas pour autant que si un élève se trouve à un certain niveau il aura validé le précédent. Mais surtout ils montrent que le sens spatial est indissociable de l'apprentissage de la géométrie.

Apprentissage en mathématiques : géométrie et sens spatial

Les trois modèles évoqués montrent que les connaissances géométriques et spatiales sont très proches. De ce fait en mathématiques, il est indispensable de traiter la géométrie avec le développement des connaissances spatiales. Ce que le CREM définit par:

« La géométrie, qui a souvent (et longtemps) été cantonnée à l’enseignement du raisonnement logique et de la méthode hypothético-déductive, retrouve ainsi (à présent) son attrait visuel et l’un de ces rôles fondamentaux, l’organisation et la structuration de l’espace. » (CREM, 2004).

Cette étude conjointe du sens spatial et de la géométrie nécessaire pour l'apprentissage des mathématiques est en outre vérifié par des études récentes en neurologie. Effectivement, le cerveau est divisé en deux hémisphères: − l’hémisphère droit correspondant à l’intelligence visuo-spatiale et à la vision globale, à l’imagination, aux liens, relations et associations − l’hémisphère gauche correspondant à l’intelligence linguistique et à la vision locale ou partielle Or Houdé (Houdé, 2004) a montré qu'en réalisant une activité de mathématiques, ces deux hémisphères du cerveau sont sollicitées.

De ce fait, l'activation de l'hémisphère droit lié à l'intelligence visuo-spatiale montre bien que le sens spatial est nécessaire et joue un grand rôle en mathématiques.

Ainsi, il est important de ne pas négliger cet aspect dans l'apprentissage des mathématiques plus spécifiquement en géométrie.

Références

Berthelot, R., & Salin, M. H. (1999). L’enseignement de l’espace à l’école primaire. Grand N, 65, 37-59.

Bessot, A. (1994). « Repr´esentation graphiques et maˆıtrise des rapports avec l’espace. » Actes du s´eminaire sur la repr´esentation du CIRADE, p.1-34.

Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning.

CREM : Centre de Recherche sur l’Enseignement des Mathématiques (2004) Pour une culture mathématique accessible à tous. Élaboration d’outils pédagogique pour le développement des compétences citoyennes, Nivelle, Belgique.

Hoffer, A.R. (1977). Mathematics Resource Project : Geometry and visualization. Palo Alto: Creative Publications.

Houdé O. (2004) Vers une pédagogie mieux adaptée, Cerveau & Psycho, 3, 60-63.

Izard, J. (1990). « Developing spatial skills with three-dimensional Puzzles. » Arithmetic Teacher, 37, no.6, p.44-47.

Marchand, P. (2009). Le développement du sens spatial au primaire. Bulletin de l 'AMQ.49(3), 63-79.

Parzysz, B. (1991). « Espace, G´eom´etrie et Dessin. Une ing´enierie didactique pour l’apprentissage, l’enseignement et l’utilisation de la perspective parall`ele au lyc´ee. » Recherches en didactique des math´ematiques, 11, no. 23, p.211-240.

Van Hiele, P. M. (1959). La pensée de l’enfant et la géometrie’. Bulletin de l’Association des Professeurs Mathématiques de L’Enseignement Public, 198.