STIC:STIC II - exercice 12 (Aegir)/Enseignement du rapport entre la vitesse et la distance, l'exemple du lièvre et de la tortue sur Scratch

Résumé

Dans le cadre du cours STIC II, il nous a été demandé de concevoir une séquence d'enseignement s'appuyant sur l'utilisation d'un micromonde. Ces derniers cherchent à reproduire un environnement proche de la réalité et manipulable par un utilisateur. Seymour (1987, p.79) décrit les micromondes comme des petits mondes qui sont en fait des fractions du monde réel. Dans la séquence que je présente ci-dessous, j'ai décidé de me concentrer sur un public d'apprenant jeune, de l'école primaire, et de cibler l'apprentissage sur la découverte et la compréhension du rapport entre la vitesse d'un objet et de la distance parcourue.

Séquence d'enseignement

Début de la simulation

Contenu d'apprentissage identifié

Contexte d'apprentissage

La séquence est destinée à un public plutôt jeune. On cible ici des élèves de l'école primaire. C'est au cycle d'orientation que l'apprentissage autour des mouvements rectilignes est introduit, mais il s'agit d'un phénomène que des élèves en fin d'école primaire peuvent facilement concevoir. Les utilisateurs de ce micromonde doivent aussi être capables de savoir lire en autonomie (objectif fin 4P), reconnaître les nombre jusqu'à 100 (fin 4P) et comprendre une situation de proportionnalité (7-8P). Toutes ces contraintes font que les seuls réels candidats restant sont les degrés de 7 et 8P.

Dans le cadre de cette séquence, je vais imaginer que la leçon est donnée par un enseignant seul à sa classe de 20 élèves de 8P. Les élèves seront par deux, il faut donc avoir une dizaine de tablettes ou d'ordinateurs à disposition pour lancer la simulation Scratch, ou alors changer le nombre d'élèves par groupe en fonction du nombre de machines à disposition.

Rapport entre vitesse et distance

L'objet d'apprentissage est donc le rapport entre la vitesse et la distance parcourue. Il s'agit de proposer aux élèves d'observer une situation ou deux objets se déplacent en mouvement rectiligne uniforme (MRU) et de leur donner la possibilité d'influencer les différentes variables (vitesse, point de départ) pour les amener à faire des constats sur les résultats qu'offrent les variables définies. Comme le MRU est une notion travaillée normalement qu'en de secondaire II, il faut simplifier au maximum le contenu et n'utiliser que des termes connus des élèves de 8P. On omettra alors les mesures de vitesse, introduite plus tard dans la scolarité. Seules les notions de distance et rapport multiplicatif entre deux vitesses (deux fois plus vite, quatre fois plus vite, etc.) restent.

Fonctionnement de la simulation

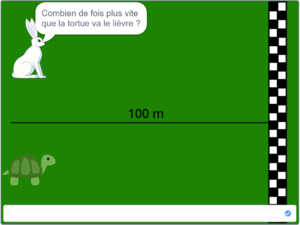
La simulation du lièvre et de la tortue a été produite sur Scratch 3.0. Elle présente un lièvre et une tortue à gauche de l'écran, se préparant à courir pour atteindre la ligne d'arrivée à droite de l'écran. Il s'agit d'un 100m. Avant de commencer la course, l'utilisateur doit répondre à deux questions :

• Combien de fois plus vite que la tortue va le lièvre : L'utilisateur rentre un nombre positif.
• Combien de mètres d'avance donnes-tu à la tortue ? : L'utilisateur rentre un nombre positif.

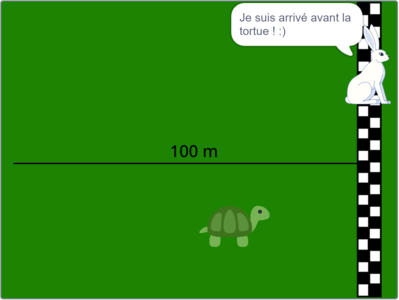
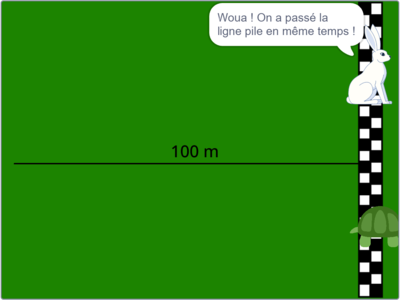
Une fois ces deux variables définies, la tortue donne le départ et les deux animaux commencent à courir tout droit vers la ligne d'arrivée. Il y a trois résolutions possibles :

1. Si le lièvre atteint la ligne avant la tortue, le lièvre dit : Je suis arrivé avant la tortue ! :)
2. Si la tortue atteint la ligne d'arrivée avant le lièvre, le lièvre dit : La tortue est arrivée avant moi... :(
3. Si le lièvre et la tortue passent la ligne en même temps, le lièvre dit : Woua ! On a passé la ligne pile en même temps !

• 

  Le lièvre gagne.

• 

  La tortue gagne.

• 

  Égalité !

Déroulement de la leçon

Pour la mise en place de la leçon, l'enseignant constitue des groupes de deux élèves et les assigne à une machine, tablette ou ordinateur, déjà ouverte sur la page Scratch de la simulation. Avant de commencer à expliquer les exercices, il peut être intéressant de rappeler brièvement l'histoire du lièvre et de la tortue pour que les élèves comprennent d'où s'inspire l'application présentée. Il peut alors expliquer le fonctionnement de la simulation aux élèves. Il faut bien penser à leur expliquer comment la relancer, en cliquant sur le petit drapeau vert. L'enseignant distribue finalement la feuille d'exercices et laisse les élèves commencer le travail. Dans les deux exercices, il faut définir les variables de façon à ce que le lièvre et la tortue passent la ligne d'arrivée en même temps.

Premier exercice

• Énoncé : Le lièvre va deux fois plus vite que la tortue. Combien de mètres d'avance faut-il donner à la tortue pour que les deux animaux passent la ligne d'arrivée en même temps ? Fais plusieurs essais jusqu'à ce que tu trouves. Note chacune de tes tentatives dans le tableau.
• Réponse recherchée : Il faut donner 50 mètres d'avance à la tortue.

Dans le premier exercice, on fixe la variable de la vitesse du lièvre en demandant aux apprenants de rentrer le nombre 2 à la première question pour que le lièvre aille deux fois plus vite que la tortue. On s'attend à ce que les élèves procèdent d'abord par tâtonnement. Le visuel de la simulation peut les aider à savoir si l'avance donnée à la tortue est proche de faire en sorte qu'elle arrive en même temps que le lapin ou non. Le raisonnement final attendu est le suivant : si le lièvre va deux fois plus vite, il peut parcourir deux fois plus de distance que la tortue avant d'arriver au même point. Si le lièvre part de 100m, la tortue ne pourra faire que la moitié, donc 50m. Le tableau à remplir par les élèves peut leur permettre de savoir qui gagne avec quelle avance de la tortue.

Deuxième exercice

• Énoncé : On donne 75 mètres d'avance à la tortue. Combien de fois plus vite que la tortue est-ce que le lièvre devra courir pour arriver sur la ligne en même temps qu'elle ? Fais plusieurs essais jusqu'à ce que tu trouves. Note chacune de tes tentatives dans le tableau.
• Réponse recherchée : Le lièvre doit aller 4 fois plus vite que la tortue.

Dans ce second exercice, on fixe l'autre variable. On demande maintenant aux élèves de trouver le multiplicateur de vitesse avec lequel le lièvre peut faire égalité avec la tortue. Les élèves de 8P connaissant l'écriture décimale des nombres, on peut leur rappeler qu'il est possible de rentrer des valeurs comme 1,5. À tâtons, les élèves risquent de trouver très vite, puisqu'ils vont logiquement essayer 1, puis 2, puis 3...

Troisième exercice (optionnel)

• Énoncé : Essaie de trouver une ou plusieurs autres combinaisons de vitesse du lièvre et d'avance de la tortue qui les font arriver en même temps sur la ligne d'arrivée. Note tes tentatives dans le tableau.
• Réponses possibles : 5x et 80m, 10x et 90m, 20x et 95m, 2,5x et 60m, ...

Cet exercice permet surtout de proposer un challenge aux groupes plus rapides. Si les élèves ont compris "le truc", ils pourront trouver quelques unes des combinaisons.

Mise en commun puis institutionnalisation du savoir

Une fois les deux premiers exercices terminés par tous les groupes, l'enseignant peut décider de les laisser essayer l'exercice optionnel ou de clore la séquence avec une discussion des réponses trouvées. Les élèves exposent leurs trouvailles et ils présentent leurs observations. L'enseignant mène la discussion, commente les réponses et en vient finalement à expliquer le calcul à faire pour définir les variables. Cela peut ressembler à :

• Ce qui est important de retenir, ce n'est pas l'avance qu'on donne à la tortue, mais la distance qui lui reste à parcourir jusqu'à l'arrivée. Si on lui donne 75m d'avance, elle doit courir 25m. Si le lapin doit parcourir 100m, on doit regarder combien de fois plus c'est que 25m. C'est le coefficient de proportionnalité. 100m c'est 4 fois plus que 25m. Le lapin doit donc courir 4 fois plus vite pour arriver en même temps que la tortue.
• Si on prend le premier exercice, on sait que le lapin court 2 fois plus vite que la tortue. Le coefficient de proportionnalité est 2. La tortue doit alors parcourir une distance 2 fois moins grande que le lièvre, ça veut dire la moitié. La moitié de 100m, c'est 50m.

Il faut évidemment adapter le discours en fonction des réponses précédemment apportées par les élèves, et l'adapter aussi à la vitesse de compréhension de ces derniers. Il s'agit d'un sujet complexe, on veut surtout que les élèves comprennent la correspondance entre courir deux fois plus vite est égal à parcourir une distance deux fois plus grande.

Évaluation

Évaluation des apprentissages.

S'agissant d'une leçon relativement courte, l'évaluation qu'on peut proposer doit être proportionnellement importante. La notion de proportionnalité se retrouve dans le Plan d'études romand (PER) pour les degrés 7-8P :

Résolution de problèmes multiplicatifs et divisifs : situations d'itération, liées au produit cartésien, de produit de mesures, de proportionnalité. (PER, MSN 23)

L'enseignant pourrait proposer un exercice dans la prochaine évaluation de mathématiques remettant cette même situation en scène. Pour s'assurer que les élèves aient bien compris la mise en commun final, il faut modifier quelques variables. On peut par exemple changer la distance de la course de 100m à 50m. Ainsi, il faudra que l'apprenant repense la logique et ne pourra pas s'appuyer sur les mêmes données que dans les exercices précédents. Voici une consigne possible :

• Le lièvre et la tortue veulent faire une course. Ils doivent courir un 50m. Le lièvre court deux fois plus vite que la tortue. Combien de mètres d'avance faut-il donner à la tortue pour qu'elle arrive en même temps que le lièvre sur la ligne d'arrivée ?

Les élèves sont en condition d'évaluation sur table et n'ont donc pas le droit à la simulation pour trouver la réponse. Ils doivent utiliser ce qu'ils sont appris grâce à la simulation.

Références

Conférence intercantonale de l’instruction publique (2010). MSN 23 – Résoudre des problèmes additifs et multiplicatifs (cycle 2). In Plan d’études romand. Neuchâtel : CIIP. Repéré à https://www.plandetudes.ch/web/guest/MSN_13/ Papert, S. (1987, July). Microworlds: transforming education. In Artificial intelligence and education (Vol. 1, pp. 79-94). Ablex Norwood, NJ. Récupéré de http://dailypapert.com/wp-content/uploads/2016/08/papert_microWorlds_chapter.pdf