« Cognition numérique » : différence entre les versions
(Ajout de la categorie Cognition) |
Aucun résumé des modifications |
||
| (9 versions intermédiaires par un autre utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{En construction}} | {{En construction}} | ||
La cognition numérique est un domaine de la psychologie ayant pour objet l'étude des opérations | La cognition numérique est un domaine de la psychologie ayant pour objet l'étude des opérations mentales qui sous tendent le traitement des nombres et la réalisation d'opérations numériques. | ||
== Historique == | == Historique == | ||
| Ligne 7 : | Ligne 7 : | ||
=== Modèle du triple code === | === Modèle du triple code === | ||
=== Ligne numérique mental=== | === Ligne numérique mental=== | ||
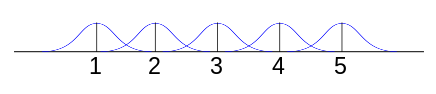
[[Fichier:Ligne num.svg|vignette|436x436px|Représentation de l'hypothèse de la ligne numérique mental. Ici la ligne va de 1 a 5, les courbe bleu représente la distribution de l'activation. Plus deux nombre sont proche en terme de magnitude, plus leurs activations respective se superpose.]] | |||
L'hypothèse de la ligne numérique mental propose que la représentation des nombres soit ordonné le long d'une ligne mental. Cette ligne serait sous tendu par par des processus cognitif de représentation spatial. Cette hypothèse a a l'origine été utilisé pour expliqué [[#L'effet de distance|l'effet de distance]] (Verguts & Fias, 2004). La version originelle de ce modèle propose que chaque nombre est associé a une distribution d'activation normale s’étendant de part et d'autre d'un point central d'activation. Ces différentes distributions serait alignée sur la ligne numérique mental de tel sorte qu'elle se superposeraient partiellement. Plus deux nombre on une magnitude proche, plus la superposition est importante, rendant ainsi la discrimination plus difficile et expliquant par la l'effet de distance (Verguts & Fias, 2004). | |||
=== Cognition spatiale et traitement numérique === | === Cognition spatiale et traitement numérique === | ||
Une série d'observations scientifiques suggère des liens entre la cognition spatial et la cognition numérique. Ce domaine s'inscrit dans le cadre de la ''Grounded Cognition'' (Barsalou, 2008). Cette théorie propose que les fonctions cognitives de ''haut niveau'' utilisent pour se développer des structures cérébrales plus ancienne d'un point de vue phylogénétique. Appliqué à la cognition numérique, l'idée serait que le traitement des nombres ferait usage des réseaux neuronaux dédié à la cognition spatial, ceci fait directement écho a l’hypothèse de la ligne numérique mental. | |||
==== SNARC effect ==== | ==== SNARC effect ==== | ||
L'effet SNARC (Spatial Numerical Association of Response Code) est le premier élément empirique montrant un lien entre le traitement des nombres et la cognition spatial. Dans une tâche ou des participants devaient juger de la parité d'un nombre (ie. juger si un nombre présenté est pair ou impair), Dehaene, Bossini et Giraux (1993) ont observé une différence de temps de réponse entre les réponses données avec la main droite ou la main gauche. Les temps de réponses étaient plus faible quand ils répondaient de la main gauche pour les petites opérande et a l'inverse les temps de réponse étaient plus lent quand les participants répondaient de la main droite pour les grandes opérande. | |||
==== Operational momentum ==== | ==== Operational momentum ==== | ||
L'operational momentum, ou inertie de l'opération, a été décrit pour la première fois par McCrinck et al. (2007). Cet effet montre la tendance des participants a sur-estimé dans le cas de calcule approximatif le résultat des addition et a sous-estimer le résultat des soustraction. Dans l'étude princeps (McCrinck et al. 2007), les participants voyaient un film présentant des additions ou soustractions de paterne de points. Le nombre de points présenté était suffisamment élevé pour que les participants ne puisse pas utiliser de stratégie de comptage. Les participants devaient ensuite dire si le résultats proposé était vrai ou faux. Pour les additions, les participants avaient tendance a accepter les résultats supérieur aux résultat correct et pour les soustractions, les participants avaient tendance a accepter les résultats inférieur aux résultats correct. | |||
==== L'effet de distance ==== | |||
L'effet de distance consiste en l'observation d'une diminution de l'exactitude des réponses et du temps de réaction pour rejeter un nombre comme étant similaire d'un référent, plus la distance entre ce nombre et le référent est faible (Moyer et Landauer, 1967; Restle, 1970). Par exemple, on demande a des participants de dire si un nombre présenté est différent de "7", lorsque le nombre présenté est "6", les participants ferons plus d'erreur et seront plus lent que quand le nombre présenté est "3". | |||
== Opérations arithmétiques == | == Opérations arithmétiques == | ||
=== | === Opération arithmétique simple et complexe === | ||
Les opération arithmétique sont constitué des additions, soustraction, multiplication et addition. La recherche en cognition numérique fait la différence entre les opération dite "simple" et "complexe". La différence porte avant tout sur la taille des opérande impliqué. Il est communément admis pour les addition et soustraction que les opérande allant de 1 a 10 ne donnent lieux qu'a des opération simple alors que les opérations complexe porte sur des opérande plus grande. Pour les multiplications et les division, on considère en générale que les opération "simple" ne porte que sur des opérandes inférieur a 5. | |||
La différence a été a l'origine proposé par Groen et Parkman (1972), ces auteurs ont expliqué [[#L'effet de taille|l'effet de taille]] en postulant un mécanisme de récupération direct en mémoire pour les opérations dites "simple". En effet, les pentes observé étaient d'environ 20 millisecondes par incrément, ce temps fut jugé trop rapide pour une procédure algorithmique. A l'inverse, les opérations dites "complexe", c'est a dire impliquant des grand nombres, sont résolu par de tel procédure. L'argument principal en faveur de cela est que ces procédures sont conscientes. Par exemple, résoudre le problème 43+24+56 implique une série d'action dont on a conscience. Au contraire, une partie important de la population a l'impression de ne pas utiliser des procédures de comptages quand ils font par exemple 2+3. | |||
=== L'effet de taille === | === L'effet de taille === | ||
L'effet de taille (size effect) a été pour la première fois observé par Groen et Parkman en 1972. Cet effet a eu une incidence considérable sur l'étude de l'arithmétique mental. Cet effet consiste en l'observation que le temps de réponse et le taux d'erreur lors de la réalisation d'une addition augmente avec l'augmentation de la taille des opérandes. | |||
=== Modèle de récupération direct en mémoire === | === Modèle de récupération direct en mémoire === | ||
=== Procédure automatisé === | === Procédure automatisé === | ||
== Bilbiographie == | == Bilbiographie == | ||
Barsalou, L. W. (2008). Grounded Cognition. Annual Review of Psychology, 59(1), 617-645. http://doi.org/10.1146/annurev.psych.59.103006.093639 | |||
Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal Of Experimental Psychology: General, 122(3), 371-396. http://doi.org/10.1037/0096-3445.122.3.371 | |||
Groen, G. J., & Parkman, J. M. (1972). A chronometric analysis of simple addition. Psychological Review, 79(4), 329-343. http://doi.org/10.1037/h0032950 | |||
McCrink, K., Dehaene, S., & Dehaene-Lambertz, G. (2007). Moving along the number line:Operational momentum in nonsymbolic arithmetic. Perception & psychophysics,69(8), 1324–1333. | |||
Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature. | |||
Pesenti, M., & Seron, X. (2004). La cognition numérique. | |||
Restle, F. (1970). Speed of adding and comparing numbers. Journal of Experimental Psychology, 83(2p1), 274. | |||
Verguts, T., & Fias, W. (2004). Representation of number in animals and humans: A neural model. Journal of cognitive neuroscience, 16(9), 1493-1504. | |||
[[Catégorie:Cognition]] | [[Catégorie:Cognition]] | ||
Dernière version du 28 janvier 2020 à 16:47
Cet article est en construction: un auteur est en train de le modifier.
En principe, le ou les auteurs en question devraient bientôt présenter une meilleure version.
La cognition numérique est un domaine de la psychologie ayant pour objet l'étude des opérations mentales qui sous tendent le traitement des nombres et la réalisation d'opérations numériques.
Historique
Représentation des nombres
Modèle du triple code
Ligne numérique mental
L'hypothèse de la ligne numérique mental propose que la représentation des nombres soit ordonné le long d'une ligne mental. Cette ligne serait sous tendu par par des processus cognitif de représentation spatial. Cette hypothèse a a l'origine été utilisé pour expliqué l'effet de distance (Verguts & Fias, 2004). La version originelle de ce modèle propose que chaque nombre est associé a une distribution d'activation normale s’étendant de part et d'autre d'un point central d'activation. Ces différentes distributions serait alignée sur la ligne numérique mental de tel sorte qu'elle se superposeraient partiellement. Plus deux nombre on une magnitude proche, plus la superposition est importante, rendant ainsi la discrimination plus difficile et expliquant par la l'effet de distance (Verguts & Fias, 2004).
Cognition spatiale et traitement numérique
Une série d'observations scientifiques suggère des liens entre la cognition spatial et la cognition numérique. Ce domaine s'inscrit dans le cadre de la Grounded Cognition (Barsalou, 2008). Cette théorie propose que les fonctions cognitives de haut niveau utilisent pour se développer des structures cérébrales plus ancienne d'un point de vue phylogénétique. Appliqué à la cognition numérique, l'idée serait que le traitement des nombres ferait usage des réseaux neuronaux dédié à la cognition spatial, ceci fait directement écho a l’hypothèse de la ligne numérique mental.
SNARC effect
L'effet SNARC (Spatial Numerical Association of Response Code) est le premier élément empirique montrant un lien entre le traitement des nombres et la cognition spatial. Dans une tâche ou des participants devaient juger de la parité d'un nombre (ie. juger si un nombre présenté est pair ou impair), Dehaene, Bossini et Giraux (1993) ont observé une différence de temps de réponse entre les réponses données avec la main droite ou la main gauche. Les temps de réponses étaient plus faible quand ils répondaient de la main gauche pour les petites opérande et a l'inverse les temps de réponse étaient plus lent quand les participants répondaient de la main droite pour les grandes opérande.
Operational momentum
L'operational momentum, ou inertie de l'opération, a été décrit pour la première fois par McCrinck et al. (2007). Cet effet montre la tendance des participants a sur-estimé dans le cas de calcule approximatif le résultat des addition et a sous-estimer le résultat des soustraction. Dans l'étude princeps (McCrinck et al. 2007), les participants voyaient un film présentant des additions ou soustractions de paterne de points. Le nombre de points présenté était suffisamment élevé pour que les participants ne puisse pas utiliser de stratégie de comptage. Les participants devaient ensuite dire si le résultats proposé était vrai ou faux. Pour les additions, les participants avaient tendance a accepter les résultats supérieur aux résultat correct et pour les soustractions, les participants avaient tendance a accepter les résultats inférieur aux résultats correct.
L'effet de distance
L'effet de distance consiste en l'observation d'une diminution de l'exactitude des réponses et du temps de réaction pour rejeter un nombre comme étant similaire d'un référent, plus la distance entre ce nombre et le référent est faible (Moyer et Landauer, 1967; Restle, 1970). Par exemple, on demande a des participants de dire si un nombre présenté est différent de "7", lorsque le nombre présenté est "6", les participants ferons plus d'erreur et seront plus lent que quand le nombre présenté est "3".
Opérations arithmétiques
Opération arithmétique simple et complexe
Les opération arithmétique sont constitué des additions, soustraction, multiplication et addition. La recherche en cognition numérique fait la différence entre les opération dite "simple" et "complexe". La différence porte avant tout sur la taille des opérande impliqué. Il est communément admis pour les addition et soustraction que les opérande allant de 1 a 10 ne donnent lieux qu'a des opération simple alors que les opérations complexe porte sur des opérande plus grande. Pour les multiplications et les division, on considère en générale que les opération "simple" ne porte que sur des opérandes inférieur a 5.
La différence a été a l'origine proposé par Groen et Parkman (1972), ces auteurs ont expliqué l'effet de taille en postulant un mécanisme de récupération direct en mémoire pour les opérations dites "simple". En effet, les pentes observé étaient d'environ 20 millisecondes par incrément, ce temps fut jugé trop rapide pour une procédure algorithmique. A l'inverse, les opérations dites "complexe", c'est a dire impliquant des grand nombres, sont résolu par de tel procédure. L'argument principal en faveur de cela est que ces procédures sont conscientes. Par exemple, résoudre le problème 43+24+56 implique une série d'action dont on a conscience. Au contraire, une partie important de la population a l'impression de ne pas utiliser des procédures de comptages quand ils font par exemple 2+3.
L'effet de taille
L'effet de taille (size effect) a été pour la première fois observé par Groen et Parkman en 1972. Cet effet a eu une incidence considérable sur l'étude de l'arithmétique mental. Cet effet consiste en l'observation que le temps de réponse et le taux d'erreur lors de la réalisation d'une addition augmente avec l'augmentation de la taille des opérandes.
Modèle de récupération direct en mémoire
Procédure automatisé
Bilbiographie
Barsalou, L. W. (2008). Grounded Cognition. Annual Review of Psychology, 59(1), 617-645. http://doi.org/10.1146/annurev.psych.59.103006.093639
Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal Of Experimental Psychology: General, 122(3), 371-396. http://doi.org/10.1037/0096-3445.122.3.371
Groen, G. J., & Parkman, J. M. (1972). A chronometric analysis of simple addition. Psychological Review, 79(4), 329-343. http://doi.org/10.1037/h0032950
McCrink, K., Dehaene, S., & Dehaene-Lambertz, G. (2007). Moving along the number line:Operational momentum in nonsymbolic arithmetic. Perception & psychophysics,69(8), 1324–1333.
Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature.
Pesenti, M., & Seron, X. (2004). La cognition numérique.
Restle, F. (1970). Speed of adding and comparing numbers. Journal of Experimental Psychology, 83(2p1), 274.
Verguts, T., & Fias, W. (2004). Representation of number in animals and humans: A neural model. Journal of cognitive neuroscience, 16(9), 1493-1504.