Parable of the polygons
Parable of the polygons est un billet de blog interactif portant sur la tolérance et la ségrégation.
Description
Contenu enseigné
Parable of the polygons est un jeu qui a pour but de nous montrer, comme le disent ses créatrices, « how harmless choices can make a harmful world », c’est-à-dire comment des choix innocents peuvent produire un monde nocif.
Dans un premier temps, le jeu a pour but d’expliquer et d’illustrer un modèle mathématique de ségrégation créé par Schelling (1971). L’objectif est de voir l’impact de la somme des choix individuels sur le fonctionnement de la société en général. Dans un second temps, les autrices nous exposent par quel moyen il est possible de réduire ce phénomène de ségrégation, et ainsi, comment augmenter la diversité dans notre société.
Mécaniques de jeu
Mécaniques principales, secondaires et annexes
Le jeu se joue seul. Globalement, il consiste en une succession de séquences de lecture et de jeu selon le schéma suivant:
Dans un premier temps, la mécanique principale est fondée sur du drag-and-drop : il faut déplacer les personnages mécontents jusqu’à ce qu’ils deviennent « souriants » ou « neutres ». Une fois qu’ils ne sont plus malheureux, il devient impossible de les déplacer. Les paramètres qui rendent malheureux les polygones peuvent varier (1/3 de voisins différents, 3/4 de voisins différents, etc).
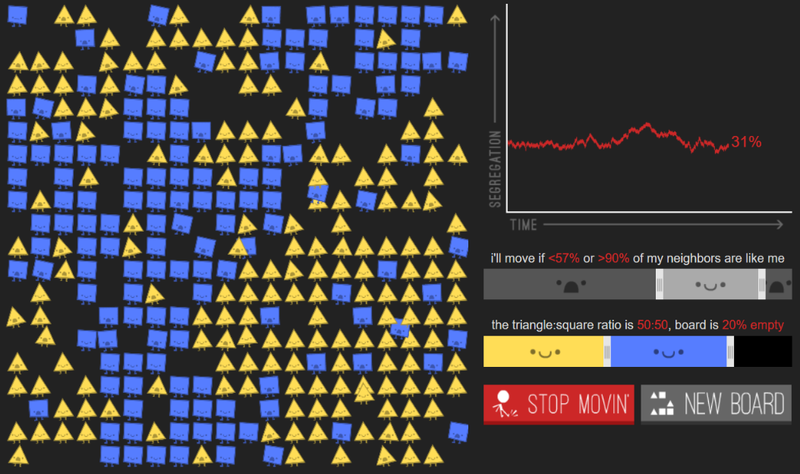
Ensuite, les tableaux s’agrandissent (on passe de tableau de 3x3 personnages à des tableaux de 20x20) et de plus en plus de paramètres sont introduits. A ce moment là, le jeu nous propose de déplacer automatiquement les personnages mécontents dans les zones vides disponibles. Le jeu devient automatisé et le drag-and-drop devient une mécanique secondaire. Sur ce type de tableaux, le jeu se rapproche beaucoup d’une simulation.
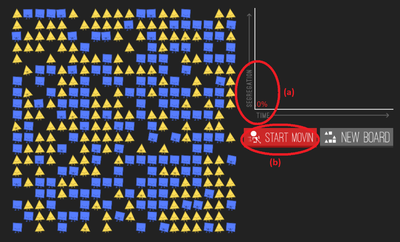
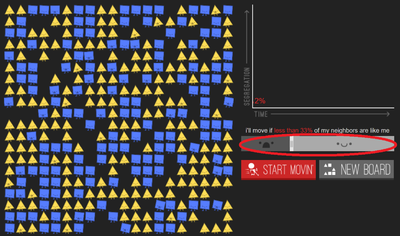
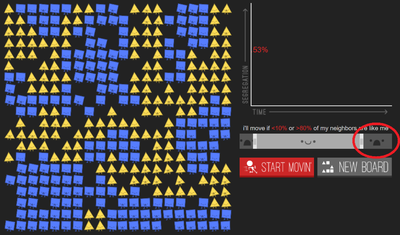
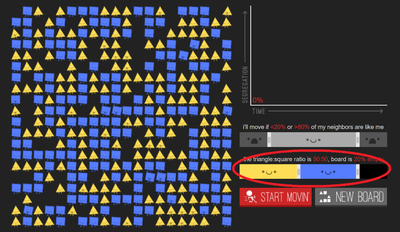
Ci-dessous un tableau récapitulatif des éléments introduits (entourés en rouge) à chaque étape du jeu :
| 1 | Le joueur doit déplacer les formes par du drag and drop pour qu’elles soient contentes.
Il peut faire varier la répartition géographique initiale de la population, grâce au bouton « New board » ; |
 |
| 2 | Introduction d'un graphique représentant la ségrégation en fonction du temps (a) ainsi que de l'automatisation des déplacements des personnages (b) et de la possibilité de suspendre l'évolution pour observer l'état de la population grâce au bouton « stop movin » | 
|
| 3 | Introduction de la possibilité pour le joueur de régler / jouer avec le seuil de tolérance des personnages | 
|
| 4 | Idem 3, mais avec des conditions initiales imposées par le jeu : une population clivée | 
|
| 5 | Introduction du paramètre « recherche de la diversité », réglable par le joueur | 
|
| 6 | Introduction du dernier paramètre : choix de la proportion initiale de triangles et de carrés dans la population. Le jeu devient un bac à sable | 
|
Le jeu se termine sur un message qui synthétise les différents concepts qui ont été présentés.
Pendant les phases de jeu, aucun objectif de performance n'est fixé: le joueur n’est pas obligé d'aller vite, il n’y a pas de limites au de nombre de déplacements. On peut avancer dans le jeu sans condition: le joueur peut à tout moment passer d’un tableau à l’autre. Il peut aussi bien éviter les phases de simulation que les phases de lecture. Le jeu est dépourvu de score, il n’y a pas de feed-back d’échec (excepté la persistance des visages mécontents des personnages), et les feed-back de réussite sont très discrets (l’écran tilt pendant une demi-seconde quand plus aucun des personnages n’est mécontent). Mais on comprend rapidement que la démonstration n'a d'intérêt que si l'on l'ordre de défilement du jeu. Il correspond à une augmentation progressive de la complexité, soit par le nombre de variables à régler, soit par la nature du feed-back (image ou graphique dynamique).
Habillage (média, monde fictionnel, récit)
Il n’y a pas vraiment d’histoire dans ce jeu. Il se présente sous la forme d’un billet de blog interactif : il y a d’abord une explication sur un phénomène social (qui sert aussi de didacticiel pour la partie simulation), puis une partie jeu (ou simulation). À la fin d’une phase de simulation, il y a un texte qui fait office de débriefing, puis un nouveau concept est présenté. Les phases de jeux sont ainsi intégrées à la page entre deux paraphes de texte. Les écrans sont simples, lisibles. Chaque séquence (plateau ou récit) tient complètement dans un seul écran.
Le monde est très épuré : L'univers est très sobre, en 2D, sans musique ni bruitage. Il se limite au stricte nécessaire, avec un décor minimaliste: seulement des fonds noir ou blanc sur lesquels sont disposés les personnages. Les autrices ont tout de même créé une espèce de monde fictionnel constitué de personnages : les triangles jaunes et les carrés bleus. Ils possèdent des yeux qui clignotent et une bouche qui montre leur émotion. Ils oscillent en permanence, ce qui les rend plus vivants et sympathiques. Ils font office d’allégorie permettant de mettre en évidence les différences humaines. Il est intéressant de noter que ces personnages sont utilisés dans d’autres jeux de Nicky Case (comme dans To build a better Ballot par exemple).
Stratégies
Il est difficile de déterminer quels styles de stratégies doivent émerger du jeu. En effet, comme dit plus haut, il n’y a pas de score ni de feed-back de réussite ou d'échec, et il nous est possible de passer d’une phase de lecture à l’autre sans passer par le jeu. En somme, le joueur n’est pas poussé à développer des stratégies pour résoudre les tableaux (puisque ce n’est pas le “vrai” but du jeu), mais il est plutôt invité à explorer les différents paramètres de la simulation.
Environnement informatique
L’environnement informatique de ce jeu est une page web. Plus précisément, comme le qualifie son autrice Nicky Case, c’est un post de blog jouable. Tout le jeu a été développé en HTML5, CSS et javascript.
Ce jeu est donc jouable sur tous les navigateurs. Toutefois, mieux vaut privilégier l’ordinateur: certaines mécaniques du jeu sont très limitées, voire indisponibles avec certains navigateurs sur mobile.
Accès (lien, éditeur, prix)
Le jeu est disponible gratuitement sur le web à l'adresse suivante : https://ncase.me/polygons/ et ne nécessite aucune installation. Il a été traduit dans 16 langues (dont le français).
Le jeu a été créé par Victoria Hart (alias Vi Hart), une vidéaste vulgarisatrice de mathématique et Nicky Case, une game-designeuse, qui a conçu plusieurs autres jeux basés sur des articles scientifiques. Il est édité sous licence Creative Commons (CC0 1.0). Il est donc libre et gratuit, et son code est en open source.
Principes pédagogiques
Apprentissage actif
Le recours à des simulations s'inscrit fortement dans une démarche expérimentale, scientifique, qui met en œuvre des raisonnements inductifs : on émet des hypothèses, on les expérimente, on observe les résultats et on essaie d'en tirer une généralité, un modèle.
Les autrices du post (qui font figure d’enseignantes) suggèrent des configurations de personnages particulières qui permettent à l’apprenant de comprendre de nouveaux principes par essais successifs. En effet, lors des phases de jeu, le joueur apprend par sa propre activité : le déplacement des personnages va lui offrir la possibilité de déduire seul les mécanismes liés à la ségrégation. Les enseignantes vont ensuite « débriefer » et reformuler les conclusions que je joueur « devrait » s’être fait pendant la phase de jeu.
Approche constructiviste
On peut aussi voir que les principes pédagogiques de ce jeu peuvent s’inscrire dans une approche constructiviste : en effet, le jeu commence avec des principes simples. Dès que ces derniers sont intégrés, on en souligne les limites ou l’on met en avant des résultats contre-intuitifs issus du dispositif de simulation (par exemple, lorsque l'on constate que si la population est déjà ségrégée, diminuer le seuil d'intolérance ne sert à rien).
Ces éléments vont générer du conflit cognitif, ce qui obligera le joueur à repenser sa conception des principes présentés. Ceci va pousser l’apprenant vers un nouveau niveau de compréhension du phénomène.
Approche transmissive
Parable of the polygons offre au joueur un guidage très fort. En effet, si le joueur ne parvient pas à formuler les conclusions partielles et générales par lui-même, elles seront données par le jeu directement.
On peut ainsi interpréter ce jeu comme ancré dans une approche transmissive : en effet, les phases explicatives peuvent être perçues comme venant d’un enseignant porteur de savoir qui donne l’information réelle, la vérité, à l’apprenant. De même, les phases de jeu peuvent être interprétées comme des vérifications du savoir qui vient d’être transmis.
Intégration du contenu enseigné dans le jeu
On est en droit de se poser la question de la qualité de l’intégration du contenu pédagogique de ce jeu. En effet, la “réussite” des phases niveaux ne dépend pas forcément des savoirs qui ont été expliqués précédemment (dans la phase écrite) : il est possible de déduire où placer les personnages dans le tableau sans avoir lu le texte le précédant. Dans les parties simulation, il ne faut “que” cliquer sur un bouton et observer l’effet.
Aussi, la discrétion des feedback et le fait que certains paramètres de simulation soient insolubles ne permettent pas vraiment au joueur de déduire les principes qui génèrent la ségrégation sans avoir lu les textes. En somme, les parties “jeu” n’ont un sens pédagogique qu’à la lumière des textes qui les précèdent. Certaines informations pourraient être intégrées directement dans les phases simulation (en tant que feedback par exemple) plutôt que dans les explications.
Cela dit, le contenu pédagogique (ici, la compréhension des modèles mathématiques de ségrégation) est tout de même intégré à travers le média lui-même. La partie écrite du site permet aux autrices d’exposer la recherche de Schelling (1971) et de transmettre leur point de vue personnel.
On peut donc estimer que Parable of the polygons est une très bonne synthèse d’article interactive: Il y a un guidage fort, avec des conclusions partielles et une synthèse finale de ce que le joueur doit retenir. En revanche, si on le considère comme un jeu vidéo pédagogique, alors l’intégration n’est pas optimale.
Points forts et point faibles
Points forts
- C’est un outil pédagogique fort intéressant. En classe, par exemple, il peut être à la base d'une discussion entre élèves dans une séquence pédagogique.
- Il délivre un message optimiste au final : un peu de pro-activité dans la recherche de diversité diminue la ségrégation dans la société.
- Il est très épuré et design
- Il est gratuit
- Il aide à la compréhension de notre monde contemporain. Ce jeu une très bonne illustration des principes mis en évidence par Schelling (1971): certains tableaux qu’on obtient sont extrêmement proches de ses résultats
- Il permet de représenter visuellement des principes abstraits
Points faibles
- La formulation des conditions initiales n'est pas toujours évidente
- Les actions du joueur sont très limitées ; elles consistent essentiellement à régler des seuils.
- Une fois que le jeu est terminé, que les conclusions sont connues, il n'y a pas vraiment d'intérêt à y jouer de nouveau : aucun défi à relever
- peu utilisable sur smartphone
Logiciels similaires
Sur le site de Nicky Case (une des deux créatrices du jeu), plusieurs jeux du même type sont accessibles, comme par exemple The evolution of trust, ou encore The wisdom and/or madness of crowd. The wisdom and/or madness of crowds a d’ailleurs l’avantage d’être plus proche du jeu que de la simulation. En effet, la logique de niveau y est beaucoup plus saillante (avec des objectifs et des feedback plus clairs). Par exemple, pour passer d’un concept à un autre, il faut impérativement réussir le tableau proposé, ce qui rend la lecture des textes indispensable à la réussite du niveau.
Voici 2 jeux analysés dans le cadre du MALTT qui reposent aussi sur des simulations:
Bibliographie
Schelling, T. C. (1971). Dynamic models of segregation. Journal of mathematical sociology, 1(2), 143-186.
Signature
Page réalisée par Christelle Melchiorre-Braz et Didier Dorsaz