Conjecture map: Difference between revisions
m (using an external editor) |
m (using an external editor) |
||
| Line 43: | Line 43: | ||
== Other exemples == | == Other exemples == | ||
=== DUAL-T conjecture map about learning to write === | |||
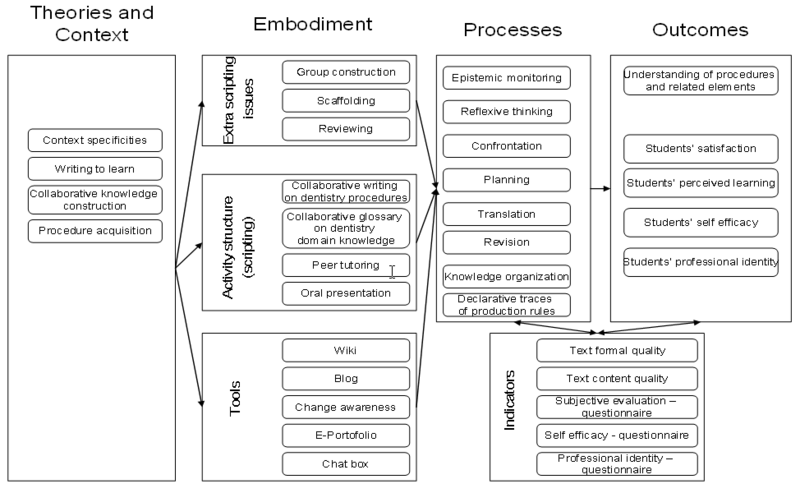
Below is an example from the [http://dualt.epfl.ch/ DUAL-T] project | Below is an example from the [http://dualt.epfl.ch/ DUAL-T] project, that provides a sort of "macro view" of a project without providing relation details. | ||
[[image:dualt-writing-to-learn-conjecture-map.png|thumb|800px|none|Conjecture map example for the DUAL-T collaborative writing framework]] | [[image:dualt-writing-to-learn-conjecture-map.png|thumb|800px|none|Conjecture map example for the DUAL-T collaborative writing framework]] | ||
[[User:Daniel K. Schneider|Daniel K. Schneider]] suggests to (sometimes) add a fifth column to separate activity design from tools design. Both together form a cognitive instrument, but to get/configure affordable tools can be a research problem by itself. | === Multiple maps for a single project === | ||
[[User:Daniel K. Schneider|Daniel K. Schneider]] suggests to (sometimes) add a fifth column to separate activity design from tools design. Both together form a cognitive instrument, but to get/configure affordable tools can be a research problem by itself. We also suggest to use maps at various levels of granularity and to break them apart if they become too complex or in order to focus on some more specific research questions. | |||
<table border="1"> | <table border="1"> | ||
Revision as of 11:13, 8 January 2010
Introduction
A Conjecture map is a research planning and organization tool used in design-based research.
According to Sandoval (2004a:abstract), “designed learning environments embody conjectures about learning and instruction, and the empirical study of learning environments allows such conjectures to be refined over time. The construct of embodied conjecture is introduced as a way to demonstrate the theoretical nature of learning environment design, and to frame methodological issues in studying such conjectures.”
"Design" in this context refers to to interventions, including designed technologies, curricular materials, and participation structures. More precisely, “designed learning environments embody design conjectures about how to support learning in a specific context, that are themselves based on theoretical conjectures of how learning occurs in particular domains. Learning theory is often underspecified with respect to learning environment design and the educational research should understand the formulation of appropriate design conjectures as theoretical activity.”
An embodied conjecture is a conjecture about how theoretical propositions might be reified within designed environments to support learning. Designed environments include tools (like software), materials, and activity structures (defined as the combination of task structure, how a task is organized, and social participation structures, Erickson, 1982).
Embodied conjectures should predict outcomes at two levels:
- intermediate outcomes are observable patterns of behavior predicted by a model of how an embodied conjecture functions should support learning.
- intervention outcomes, refer to the sort of outcome that psychologists look for, e.g. whether students learn what they are intended to learn.
Embodied conjectures also should predict interactions with their contexts of use.
The idea of a conjecture map is to link design elements to "intermediary variables" to desired outcomes. Each link is a kind of hypothesis for which various kinds of data could provide some support.
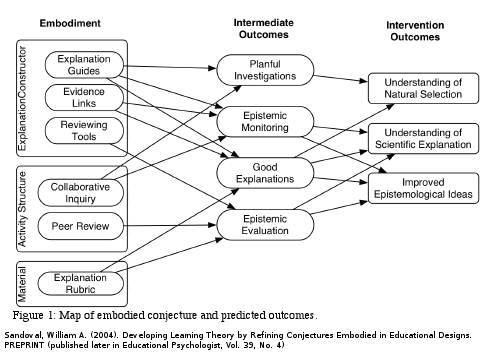
The BGUILE example
Conjecture maps were developed retrospectively at later stages of the BGuILE project.
“ExplanationConstructor and related aspects of the BGuILE learning environment were designed by conjecturing that epistemological conceptions influence scientific inquiry to the extent that they frame particular goals for the kinds of knowledge inquiry can generate, while such ideas are practically helpful only to the extent that conceptual knowledge of particular domains can generate possible explanations and investigative strategies. This conjecture led to the design conjecture to integrate conceptual and epistemic scaffolds for inquiry, which was predicted to help students both learn a particular science topic and about scientific epistemology.” (Sandoval 2004a).
It also may be useful to link design elements (embodied conjectures) to general learning and instructional theory. Here is a skeleton to get started:
| Theoretical conjectures | Embodied conjectures | Intermediate outcomes | Objective outcomes |
|---|---|---|---|
| General theory not embodied, not operational |
Design elements: Rather features than just "names" |
What's happening ? What students and teachers do |
What students will learn |
Other exemples
DUAL-T conjecture map about learning to write
Below is an example from the DUAL-T project, that provides a sort of "macro view" of a project without providing relation details.
Multiple maps for a single project
Daniel K. Schneider suggests to (sometimes) add a fifth column to separate activity design from tools design. Both together form a cognitive instrument, but to get/configure affordable tools can be a research problem by itself. We also suggest to use maps at various levels of granularity and to break them apart if they become too complex or in order to focus on some more specific research questions.
| Theoretical conjectures | Embodied conjectures - activity types |
Embodied conjectures - tools |
Intermediate outcomes | Objective outcomes |
|---|---|---|---|---|
| General theory not embodied, not operational |
Design elements: Teacher and learner activity elements |
Design elements: Tools with features (e.g. software modules) |
What's happening ? What students and teachers do |
What students will learn |
Such a design was used in Barbara Class (2009) PhD Thesis. Another methodological finding from this dissertation was that conjecture maps could be used at several levels of granularity (p. 136 ss.). We shall present a few excepts below.
(1) To provide a detailed picture of the relationship between research questions, theoretical conjectures, design elements/embodied conjectures, processes and outcomes (as suggested by Sandoval).
(2) To provide an overview of all theoretically grounded design elements as well as their expected impact on processes and outcomes. In the conjecture map they are not linked in a one-to-one relationship with design elements/embodied conjectures, since each course module implements different (selected) design elements. Design elements are linked to enabling tools.
(3) The third use of conjecture maps, in order to provide a detailed picture of each module, consists in using the same categories as above but zooming into the conjecture map to better understand how the design was actually implemented and which particular tools were used.
Alternatives
Alternatives to conjecture maps are tables like the one that is used by Jianwei Zhang et al. (2007:112) and presented in summarized form in the the knowledge-building community model article.
Bibliography
- Class, Barbara (2009). A Blended Socio-Constructivist Course with an Activity-Based, Collaborative Learning Environment Intended for Trainers of Conference Interpreters, PhD dissertation 420, Faculté de psychologie et des sciences de l'éducation, Université de Genève.
- Sandoval, William A. & Philip Bell (2004), Design-Based Research Methods for Studying Learning in Context: Introduction, Educational Psychologist, Vol. 39, No. 4: pages 199-201. doi:10.1207/s15326985ep3904_3
- Sandoval, W. A., & Bell, P. (Eds.). (2004). Design-based research methods for studying learning in context. [Special Issue] Educational Psychologist, 39(4).
- Sandoval, William A. (2004a). Developing Learning Theory by Refining Conjectures Embodied in Educational Designs, Preprint. [To appear in Educational Psychologist, Vol. 39, No. 4, Pages 213-223, see below]
- Sandoval, William A. (2004). Developing Learning Theory by Refining Conjectures Embodied in Educational Designs, Educational Psychologist, Vol. 39, No. 4, Pages 213-223.