Inkscape - Equations paramétriques, L-system et chemin

Introduction

Inkscape dispose de fonctionnalités permettant de générer des courbes paramétriques ou des fractals grâce à la grammaire des systèmes de Lindenmayer.

L'intérêt de ces fonctionnalité est que cela représente un plus grand niveau d'abstraction, et permet de pouvoir interagir directement sur les équations mathématiques de la forme désirée. De plus, la grammaire générative de Lindenmayer permet de créer rapidement des motifs géométriques complexes particulièrement adapté pour la broderie.

Courbes paramétriques

Les équations paramétriques sont des équations de type (x=f(t), y=g(t)) (dans un espace plan), x et y étant les coordonnées d'un ensemble géométrique dans l'espace vectoriel $(0,e_{1},e_{2})$.

Par exemple l'équation paramétrique d'un cercle de rayon r est $C={\begin{cases}x=r\cos(t)\\y=rsin(t)\end{cases}}t\epsilon [0,2\Pi ]$

Tracer le référentiel

Avant de pouvoir tracer une courbe paramétrique dans inkscape, il est nécessaire de dessiner un rectangle qui représentera le domaine dans laquelle la courbe paramétrique sera tracée. La largeur du rectangle correspondra à l'intervalle sur l'axe des abscisses et la hauteur du rectangle à l'intervalle des ordonnées. Si l'on souhaite que les graduations soient équivalente sur l'abscisse et l'ordonnée, il peut être plus aisé de tracer un carré (maintenir la touche ctrl en traçant le rectangle).

Paramétrer le référentiel

Sélectionner le carré ou le rectangle.

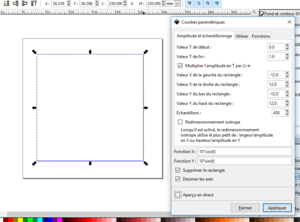
Aller dans le menu extensions -> rendu puis sélectionner courbe paramétrique.Un tableau intitulé courbe paramétrique apparaît.

Tableau de paramétrage des courbes paramétriques sur Inkscape

1. "Valeur X à gauche du rectangle" et "Valeur X à droite du rectangle" permet d'indiquer respectivement la borne inférieur, respectivement la borne supérieure de l'axe des abscisses.
2. "Valeur Y en bas du rectangle" et "Valeur Y en haut du rectangle" permet d'indiquer respectivement la borne inférieur, respectivement la borne supérieure de l'axe des ordonnées.
3. la case à cocher "supprimer le rectangle, permet de supprimer le rectangle qui délimite la courbe paramétrique, une fois celle-ci tracée.
4. la case à cocher "dessiner les axes" permet d'afficher l'axe des abscisses et des ordonnées en même temps que la courbe paramétrique.

Paramètres de la fonction

Sélectionner le carré ou le rectangle.

Aller dans le menu extensions -> rendu puis sélectionner courbe paramétrique.Un tableau intitulé courbe paramétrique apparaît.

1. Valeur de T début et valeur de T fin indique les bornes inférieures et supérieures de votre variable (par exemple pour un cercle T=[0,2 π])
2. Si votre équation est en coordonnées polaires et l'angle est votre variable, il est possible de cocher la case multiplier l'amplitude par 2π. Par exemple , en reprenant l'équation du cercle, nous pouvons sélectionner les bornes [0,1] pour T et cocher la case. Inkscape tracera le cercle pour l'angle compris dans l'intervalle [0x2 π, 1x2 π]=[0,2 π].
3. Dans la case "fonction x", il convient d'écrire l'équation paramétrique des x, puis faire de même dans la case "fonction y", pour l'équation paramétrique des y. Par exemple pour un cercle de rayon 10, il faut mettre dans "fonction x": 10*cos(t). L'onglet fonction indique l'écriture de plusieurs fonctions, à noter que π peut être utilisé en utilisant la notation "pi", de même la constante e sera notée "e".
4. Avant de valider vos paramètre, il est possible de cocher la case "Aperçu en direct" pour regarder le tracé de la courbe.
5. Lorsque la courbe est satisfaisante, il suffit de valider sur le bouton "appliquer" pour qu'Inkscape effectue le tracé.

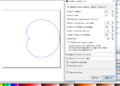
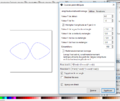
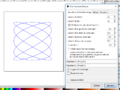
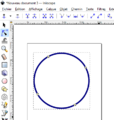
Exemples de courbes paramétriques avec Inkscape

Voici quelques exemples de tracé obtenu avec des équations paramétriques

• 

  Une cardioïde

• 

  Un lemniscate

• 

  Une rosace

• 

  Figure de Lissajou

L-système

Les L-système (ou système de Lindenmayer) sont des fractals créés à part de la grammaire générative inventé par le biologiste Lindenmayer.

Un L-système est composé d'un axiome de départ, d'un ensemble de règle et du nombre d'itérations à effectuer. Inkscape dispose de cette grammaire et il est donc possible de dessiner avec ce logiciel des fractals. Il est recommandé d'utiliser au départ un faible nombre d'itérations (4 ou 5 ) et d'augmenter progressivement sous peine de bloquer Inkscape dû aux calculs à effectuer.

L'avantage de l'utilisation des L-systèmes sur Inkscape est la possibilité de créer des motifs complexes en quelques secondes.

Terminologie

L'axiome représente l'état initial du motif

Les règles sont les règles de tranformation à appliquer à chaque élément du motif à chaque itération.

L'itération est le nombre de fois où la règle est appliqué sur les éléments du motif

Exemple:

Axiome: F

Règles: F=F+F angle 60°

La grammaire se traduit ainsi. Au départ, tracer un segment F (l'axiome). Ensuite à chaque itération, faire la transformation de chaque segment F en un segment F plus un autre segment F ayant un angle de 60° avec le premier.

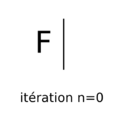
Ainsi à l'itération n=0, nous avons un segment F

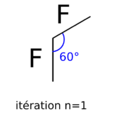
A l'itération n=1, nous avons deux segments de même longueur formant un angle de 60°

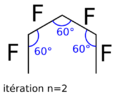
A l'itération n=2, nous avons deux fois deux segments de même longueur formant un angle de 60°,...

• 

  Fractal itération 0

• 

  Un Fractal à l'itération 1

• 

  Un fractal à l'itération 2

Grammaire du système de Lindenmayer dans Inkscape

La grammaire des système de Lindenmayer obéit à un certain nombre de règles. Par exemple, le symbole + indique d'effectuer une rotation d'un angle α.

Voici l'ensemble des règles retenues par Inkscape:

• A,B,C,D,E,F: dessiner d'un pas en avant.
• G,H,I,J,K,L: déplacer d'un pas en avant
• + : tourner dans le sens horaire d'un angle α
• -: tourner dans le sens anti-horaire d'un angle α
• I: tourner de 180°
• [: enregistrer le point
• ]retourner au point enregistré

• 

  Règles de grammaire Lindenmayer dans Inkscape

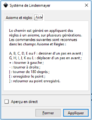
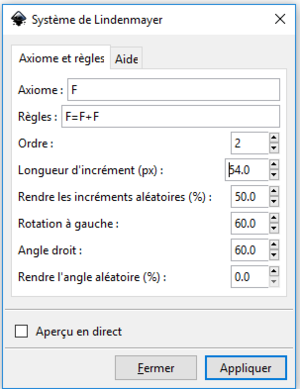
Paramétrer un L-système avec Inkscape

Pour démarrer un fractal, aller dans le menu extensions -> rendu puis sélectionner système de Lindenmayer.Un tableau intitulé système de Lindenmayer apparaît.

Le tableau de paramétrisation des systèmes de Lindenmayer

• Entrez l'axiome dans la case axiome
• Entrez la ou les règles dans la case règles. Si le fractal a plusieurs règles, celles-ci sont séparées d'un point virgule.
• Sélectionnez le nombre d'itérations dans ordre. Attention, il vaut mieux commencer avec de petites itérations (entre 3 et 5), un grand nombre itérations peut geler le programme.
• Entrer la longueur des segments dans "longueur de l'incrément".
• La case "rendre l'incrément aléatoire" permet d'indiquer les chances qu'à chaque itération, un segment change légèrement de longueur.
• "Rotation à gauche" et "Rotation à droite" indique l'angle pour tourner à gauche ou à droite
• La case à cocher "aperçu" permet de regarder le rendu du fractal avant de l'accepter.

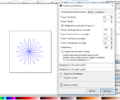
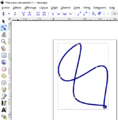
Exemple de motifs

Voici quelques fractals obtenus avec Inkscape

• 

  Triangle de Sierpinski

• 

  Une fougère de Barnsley

• 

  La courbe du dragon

Manipulations de chemins

Transformer un Objet en chemin

Pour transformer un objet en chemin sur Inkscape, il faut:

1. Sélectionner un objet
2. Sélectionner "Editer les noeuds ou les poignées de contrôle d'un chemin" ou touche F2. La souris change alors de forme.
3. Aller dans le menu "chemin" et sélectionner "Objet en chemin" ou touches ctrl+Maj+C. Des noeuds apparaissent sur l'objet sous la forme de petits carrés gris.

En sélectionnant un noeud et en le déplaçant, il entraîne une déformation de l'objet.

Plusieurs opérations sont disponible dans la barre de menu eh haut sur les noeuds. Par exemple, en déplaçant un noeud sur un autre noeud et en les sélectionnant les deux, on peut les fusionner en un seul noeud, en sélectionnant "Joindre les noeuds sélectionnés".

• 

  Transformation du cercle en chemin

• 

  Modification du chemin du cercle

Transformer un Contour en chemin

Pour transformer un contour en chemin, le processus est presque semblable à celui d'objet en chemin.

1. Sélectionner l'objet
2. Sélectionner "Editer les noeuds ou les poignées de contrôle d'un chemin" ou touche F2. La souris change alors de forme.
3. Aller dans le menu "chemin" et sélectionner "Contour en chemin" ou touches ctrl+Alt+C. Des noeuds apparaissent sur le contour de l'objet sous la forme de petits carrés gris.

En sélectionnant un des noeuds, il est possible de modifier le contour de l'objet.

• 

  Modification du contour du cercle transformé en chemin

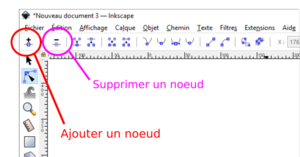
Ajout/supression de noeuds

L'ajout ou la suppression de noeuds sont des opérations très simples.

Suppression de noeuds:

1. Sélectionnez un ou plusieurs noeuds d'un chemin (petit carré gris).
2. Sélectionner dans la barre de menu "supprimer les noeuds sélectionnés". Les noeuds sont supprimés.

Ajout de noeuds de noeuds:

1. Sélectionnez deux noeuds sur un segment.
2. Sélectionner dans la barre de menu "Insérez de nouveaux noeuds au milieu des segments sélectionnés". Un nouveau noeud apparaît entre les deux noeuds sélectionnés.

Ajout-suppression noeuds