Equivalency theorem: Difference between revisions
Jump to navigation
Jump to search
m (→Introduction) |
m (→Introduction) |
||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
According to the [http://equivalencytheorem.info/?page_id=2 Equivalency Theorem] website, the theorem can be summarized with two thesis, of which the first one is more important: | According to the [http://equivalencytheorem.info/?page_id=2 Equivalency Theorem] website, the theorem (also called ''equivalence theorem'') can be summarized with two thesis, of which the first one is more important: | ||
;Thesis 1. | ;Thesis 1. | ||
Revision as of 10:11, 7 April 2015

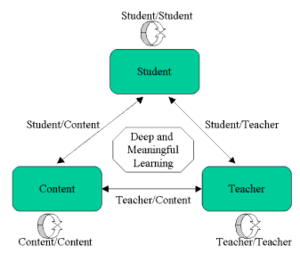
Modes of Interaction in Distance Education from Anderson and Garrison, (1998)
Introduction
According to the Equivalency Theorem website, the theorem (also called equivalence theorem) can be summarized with two thesis, of which the first one is more important:
- Thesis 1.
- Deep and meaningful formal learning is supported as long as one of the three forms of interaction (student–teacher; student–student; student–content) is at a high level. The other two may be offered at minimal levels, or even eliminated, without degrading the educational experience.
- Thesis 2.
- High levels of more than one of these three modes will likely provide a more satisfying educational experience, although these experiences may not be as cost- or time effective as less interactive learning sequences.
See also: Community of inquiry model, a complementary model by the same authors
Tools
Student-teacher (ST), Student-Student (SS) and Student-Content (SC) can be described at three levels: High, mid and low.
The EQuiv Applications includes a few PDFs that include various learning designs modeled after combinations of different interaction patterns and levels.
E.g. the following empty 3x3 matrices allow to visualize 12 different forms (taking into account absence). At least one dimension must be high !
| High | |||
| Mid | |||
| Low | |||
| ST | SS | SC |
|---|
| High | |||
| Mid | |||
| Low | |||
| ST | SS | SC |
|---|
Links
- http://equivalencytheorem.info, the home page
Bibliography
- Anderson, T. (2003). Getting the mix right again: An updated and theoretical rationale for interaction. The International Review of Research in Open and Distance Learning (IRRODL), 4(2). HTML
- Miyazoe, T., & Anderson, T. (2010). The interaction equivalency theorem. Journal of Interactive Online Learning (JIOL), 9(2), 94-104. PDF
- Miyazoe, T. (2012.02.27). Getting the Mix Right Once Again: A Peek into the Interaction Equivalency Theorem and Interaction Design. ALT News Letter. HTML
- Related
- Weerasinghe, Thushani Alwis; Robert Ramberg and Kamalanath Priyantha Hewagamage. (2012). Inquiry-Based Learning With or Without Facilitator Interactions. The Journal of Distance Education (JDE), 26(2). HTML