X3D graphics principles

Draft

Introduction

Principles underlying X3D graphics are similar to other 3D graphic formats and APIs. In this small tutorials we attempt to provide a simplified view useful to beginners.

Representation of an object

This is (roughly) how a 3D object is "built":

1. In 3D Graphics, an object is firstly defined by vertices (i.e. points) in a three dimensional x-y-z space.
2. When those points a are linked together by lines (so-called edges) we can define a wireframe rendering of an object.
3. After the wireframe has been created, a surface or skin can be applied to the object. The surface can have many qualities: color, texture, shininess, reflectivity, etc.
4. Finally, objects are either lit or emit light. Typical objects must be lit by a light source. Rendering a lit object requires shading, a very computer intensive task.

All surfaces can be represented as a set of polygons (that are perfectly flat). Complex Polygons are most often split up into triangles by the rendering machine. In other words, three vertices, connected to the each other by three edges, define a triangle, which is the typical polygon used by rendering engines. An object is then defined by these triangle faces.

Polygons have only one side, the so-called "normal" or outside. Therefore, in X3D even flat objects (such as a sheet of paper) are always represented (as very flat) cubes. For example, a cube is composed of 12 polygons (2 triangles for each side) with their "normals" outside. A quite perfect ball, on the other hand, would be composed by thousands of triangles.

Some further information about polygons and normals are available in the OpenScad beginners tutorial

Position and orientation

The coordinate system

3D space is expressed in terms of x, y and z coordinates.

• X-axis: Width or left(-) / right(+) positioning
• Y-axis: Height or or down(-) / up(+) positioning
• Z-axis: Depth or far(-) / close (+) positioning

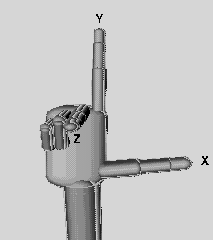
You can picture the coordinate system with the "right hand rule" also called right hand coordinate system: "x" is your thumb, "y" the index finger, and "z" the middle finger.

The right hand rule

In the picture below, the same principle is illustrated with a snapshot of an X3D scene. The blue ball is in the middle (i.e. coordinates x=0, y=0, z=0) and the viewer is positioned a bit to the right and up and looking a bit to the left.

The X3D coordinate system

Other graphics frameworks (e.g. Blender) position these coordinates differently, but an object can be rotated into the same position. Depending on how you hold your hand - fingers always stay stable - you will get a differently oriented coordinate system. To understand the difference between X3D and Blender. Imagine looking into the screen for X3D (so Z is out/in, i.e. "depth"), imagine looking down at a table for Blender (so Z is up/down, i.e. "altitude"). As a general rule it seems that CAD systems use up/down and 3D modelers either up/down or in/out (to be confirmed!)

Yet other systems use a left-hand rule. Read more about the right-hand rule in Wikipedia.

Rotation

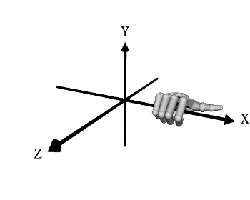
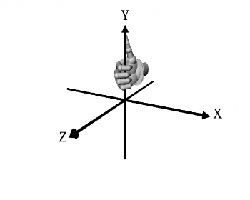
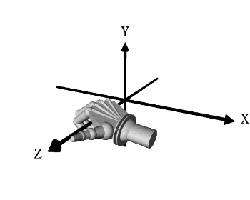
Each object can be rotated around the x, y, or z axis (or two or three of them together). The sense of the rotation is also explained with an other right hand rule.

Imagine to grabbing with your right hand an arrow representing an axis by pointing the thumb into the positive direction. Rotation is in the direction of the curling fingers.

Or as explained by "Floppy": “If you imagine wrapping your hand around one of the axes, with your thumb pointing in the positive direction, the direction of positive rotation is the same as the direction that your fingers wrap around in, i.e. clockwise looking in a positive direction. This is true for rotations about any axis, so if you want to rotate an object 90 degrees away from you around the X axis, you would use a 90 degree negative rotation.”

Rotation according to Ralph Nadau's VRML SIGGraph tutorials (1998).

Measures

• Meters
• Radians
• Seconds

The scene graph

“Scene graphs are data structures used to hierarchically organize and manage the contents of spatially oriented scene data.” (Aaron E. Walsh, 2002)

According to Don Brutzman's slides, Scene graphs are a model-centric approach to 3D that hierarchically defines geometry shape, appearance, position and orientation, etc. etc. The scene graphs has the following features:

• Directed acyclic graph (DAG), meaning a tree with a root node and no loops
• Declarative listing of parameters of interest

This concept is similar to defining a Computer Aided Design (CAD) model and very different from most imperative programming approaches that define a scene with instructions like: draw this triangle, that triangle, recompute, etc.

Since X3D is a delivery format, the scene graph also has a formal definition, in the form of a (W3C) XML DOM tree and which can be manipulated at run time through the EcmaScript API.

Again, according to Brutzman, Scene graph rendering is an iterative drawing process that works in the following way: The browser traverses the scene graph, updating any values within nodes and building an image. The new image then replaces previous screen image in a process known as double buffering. Rapid repetitions are very important, i.e. frame rate faster than 7-10 Hz (cycles per second) provides appearance of smooth motion.

Links

• Understanding Scene Graphs, By Aaron E. Walsh, July 01, 2002, Dr. Dobb's (covers VRML, Extensible 3D, MPEG-4, and Java 3D.)