Methodology tutorial - exploratory data analysis

This article or section is currently under construction

In principle, someone is working on it and there should be a better version in a not so distant future.
If you want to modify this page, please discuss it with the person working on it (see the "history")

<pageby nominor="false" comments="false"/>

This is part of the methodology tutorial (see its table of contents).

Introduction

This tutorial will provide a short introduction to exploratory data analysis and multi-variate data reduction. We will focus on:

• Looking at distributions
• Uncovering structure (both in variables and population)

There exist many techniques, here we plan (to be confirmed!) boxplots, cluster analysis and Factor Analysis (principal components).

Learning goals

• Be able to select a procedure for exploratory data analysis
• ........

Prerequisites

• Methodology tutorial - quantitative data analysis
• Methodology tutorial - descriptive statistics

Moving on

• none

Level and target population

• Beginners

Quality

• Under construction , use with care !!

Exploratory statistics

Exploratory data analysis can be defined as a set of techniques but also as a spirit.

According to NIST handbook,

exploratory Data Analysis (EDA) is an approach/philosophy for data analysis that employs a variety of techniques (mostly graphical) to

1. maximize insight into a data set;

2. uncover underlying structure;

3. extract important variables;

4. detect outliers and anomalies;

5. test underlying assumptions;

6. develop parsimonious models; and

7. determine optimal factor settings.

According to Wikipedia and referring to Tukey,

the objectives of EDA are to:

• Suggest hypotheses about the causes of observed phenomena
• Assess assumptions on which statistical inference will be based
• Support the selection of appropriate statistical tools and techniques
• Provide a basis for further data collection through surveys or experiments

Cluster Analysis

• Cluster analysis or classification refers to a set of multivariate methods for grouping elements (subjects or variables) from some finite set into clusters of similar elements (subjects or variables).

• There different kinds of cluster analysis. The most popular are : hierarchical cluster analysis and K-means cluster.

Typical use case examples: Classify teachers into 4 to 6 different groups regarding ICT usage

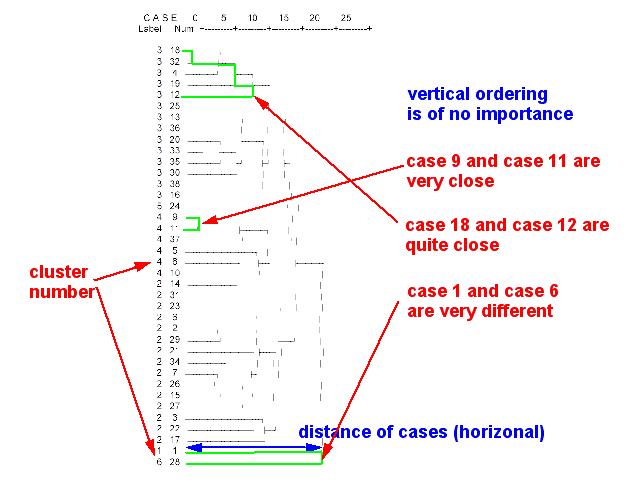
Hierarchical cluster analysis

Tries to identify similar cases in progressive steps. This procedure allows to produce a dendogram (tree diagram of the population)

Example

classification of teachers

• A hierarchical analysis of 36 survey variables allowed to identify 6 major types of teachers with respect to ICT use:
• Type 1 : The "convinced teacher" (l’enseignant convaincu)
• Type 2 : The "active teacher" (les enseignants actifs)
• Type 3 : The "motivated teacher working within a bad environment" (les enseignants motivés ne disposant pas d’un environnement favorable)
• Type 4 : The "willing but not ICT-compentent teacher" (les enseignants volontaires, mais faibles dans le domaine des technologies(
• Type 5 : The "ICT-competent teacher unwilling to use ICT in the class" (l’enseignant techniquement fort mais peu actif en TIC)
• Type 6 : The "Willing and relatively weak in ICT teacher" (l’enseignant à l’aise malgré un niveau moyen de maîtrise)

In order to come up with such labels like "convinced teacher" you have to list the means of all cluster variables and use your imagination.

Descriptive statistics of a subset of the 36 variables used for analysis:

(sorry this is hardly readable)

Links and references

• NIST/SEMATECH e-Handbook of Statistical Methods Exploratory Data Analysis, retrieved 18:22, 5 March 2009 (UTC)
• Exploratory data analysis (Wikipedia)
• Tukey, John Wilder (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 0-201-07616-0.