Equivalency theorem
Jump to navigation
Jump to search
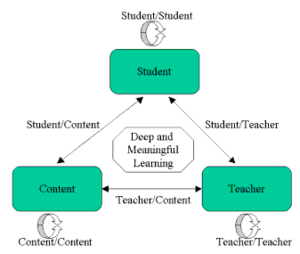
Modes of Interaction in Distance Education from Anderson and Garrison, (1998)
Introduction
According to the Equivalency Theorem website, the theorem (also called equivalence theorem) can be summarized with two thesis, of which the first one is more important:
- Thesis 1.
- Deep and meaningful formal learning is supported as long as one of the three forms of interaction (student–teacher; student–student; student–content) is at a high level. The other two may be offered at minimal levels, or even eliminated, without degrading the educational experience.
- Thesis 2.
- High levels of more than one of these three modes will likely provide a more satisfying educational experience, although these experiences may not be as cost- or time effective as less interactive learning sequences.
See also:
- Iron triangle model
- Community of inquiry model, a complementary model by the same authors
Tools
Student-teacher (ST), Student-Student (SS) and Student-Content (SC) can be described at three levels: High, mid and low.
The EQuiv Applications includes a few PDFs that include various learning designs modeled after combinations of different interaction patterns and levels.
E.g. the following empty 3x3 matrices allow to visualize 12 different forms (taking into account absence). At least one dimension must be high !
| High | |||
| Mid | |||
| Low | |||
| ST | SS | SC |
|---|
| High | |||
| Mid | |||
| Low | |||
| ST | SS | SC |
|---|
Links
- http://equivalencytheorem.info, the home page
Bibliography
- Anderson, T. (2003). Getting the mix right again: An updated and theoretical rationale for interaction. The International Review of Research in Open and Distance Learning (IRRODL), 4(2). HTML
- Lane, A 2014. Placing Students at the Heart of the Iron Triangle and the Interaction Equivalence Theorem Models. Journal of Interactive Media in Education 2014(2):5, DOI: http://dx.doi.org/10.5334/jime.ac
- Miyazoe, T., & Anderson, T. (2010). The interaction equivalency theorem. Journal of Interactive Online Learning (JIOL), 9(2), 94-104. PDF
- Miyazoe, T. (2012.02.27). Getting the Mix Right Once Again: A Peek into the Interaction Equivalency Theorem and Interaction Design. ALT News Letter. HTML
- Miyazoe, D. and Anderson, T. 2013 Interaction Equivalency in an OER, MOOCS and Informal Learning Era. Journal of Interactive Media in Education, Sep 2013: 15.
- Related
- Weerasinghe, Thushani Alwis; Robert Ramberg and Kamalanath Priyantha Hewagamage. (2012). Inquiry-Based Learning With or Without Facilitator Interactions. The Journal of Distance Education (JDE), 26(2). HTML