X3D graphics principles

Introduction

Principles underlying X3D graphics are similar to other 3D graphic formats and APIs. In this small tutorials we attempt to provide a simplified view useful to beginners.

Representation of an object

This is (roughly) how an object is built up:

1. In 3D Graphics, an object is first defined by its edges (points) in a three dimensional x-y-z space.

1. When those points a are linked together by lines we get a wireframe rendering of an object.

1. After the frame has been created, a surface or skin is applied to the object. The surface can have many qualities: color, texture, shininess, reflectivity, etc.

1. Finally, objects are either lit or emit light. Most objects have been lit by a light source and must be shaded. Shading is the most computer intensive task.

All surfaces can be represented as a set of polygons (that are perfectly flat). Complex Polygons are always split up into triangles by the rendering machine.

Polygons have only one side, the so-called "normal" or outside. Therefore, in X3D even flat objects (such as a sheet of paper) are always represented (as very flat) cubes. For example, a cube is composed of 12 polygons (2 triangles for each side) with their "normals" outside.

Position and orientation

The coordinate system

• Width (x axis) or left(-) / right(+)
• Height (y axis) or down(-) / up(+)
• Depth (z axis) or far(-) / close (+)

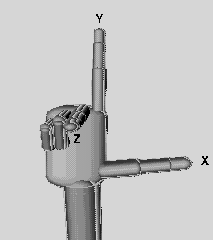
You can picture the coordinate system with the "right hand rule": "x" is your thumb, "y" the index finger, and "z" the middle finger.

The right hand rule

In the picture below, the same principle is illustrated with a snapshot of an X3D scene. The blue ball is in the middle (i.e. coordinates x=0, y=0, z=0) and the viewer is positioned a bit to the right and up and looking a bit to the left.

The X3D coordinate system

Other graphics frameworks (e.g. Blender) position these coordinates differently, but an object can be rotated into the same position. Depending on how you hold your hand - fingers always stay stable - you will get a differently oriented coordinate system. To understand the difference between X3D and Blender. Imagine looking into the screen for X3D (so Z is out/in, i.e. "depth"), imagine looking down at a table for Blender (so Z is up/down, i.e. "altitude"). As a general rule it seems that CAD systems use up/down and 3D modelers either up/down or in/out (to be confirmed!)

Yet other systems use a left-hand rule. Read more about the right-hand rule in Wikipedia.

Rotation

Each object can be rotated around the x, y, or z axis (or two or three of them together). The sense of the rotation is also explained with a right hand rule.

Imagine to graph an arrow representing an axis and turn in the direction of the closing hand (curled fingers)