Analyse de données quantitatives
| Manuel de recherche en technologie éducative | |
|---|---|
| Page d'entrée du module Analyse de données quantitatives |
|
| ◀▬▬▶ | |
| ⚐ brouillon | ☸ débutant |
| ⚒ 2018/10/01 | ⚒⚒ 2015/08/27 |
| Autres pages du module | |
Introduction
Ce module présente des analyses statistiques bivariées simples. Ces statistiques inférentielles, telles qu’on les appelle, ont pour objectif de tester les relations entre deux variables ou plus. Nous allons présenter les trois méthodes les plus utilisées pour l’analyse des relations entre deux variables.
Objectifs d’apprentissage
- Comprendre l’importance des hypothèses relatives aux données et de la mauvaise influence des valeurs atypiques éventuelles
- Comprendre le principe d’analyse statistique consistant à « révéler la structure » des données
- Être capable d’identifier les étapes importantes de l’analyse statistique (simple)
- Connaître les différences entre les quatre types de coefficients statistiques
- Être capable de choisir une procédure pour une analyse bivariée en fonction des types de données
- Être capable d’interpréter et de créer des tableaux croisés
- Être capable de comprendre et de créer des analyses de variance
- Être capable de comprendre et de créer des analyses de régression simples
Avant de se lancer dans les principes d'analyses, nous faisons un détour vers les données. En effect, un type d'analyse statistique donnée ne fonctionne pas avec toutes sortes de distributions, out dit positivent, exige un certain "modèle de données" pour correctement renseigner.
Echelles et hypothèses relatives aux données
Comme nous l’avons vu précédemment, il existe différents types de données quantitatives. Voici un rappel de ces trois types de données quantitatives:
- données nominales, i.e. les observations catégorisées (e.g. noms de pays)
- données ordinales, i.e. les classements
- données à intervalles, i.e. les observations quantitatives à l'aide d'échelles comprenant des intervalles réguliers (e.g. le résultat d’un test)
Pour chaque combinaison de types de mesures, vous devrez utiliser des techniques d’analyse spécifiques. En d’autres termes, les procédures statistiques fonctionnent pour la plupart uniquement avec certains types de données. Il existe un plus grand choix de techniques statistiques pour des variables quantitatives (à intervalles). Par conséquent, des échelles telles que (1) tout à fait d’accord, (2) d’accord, (3) plus ou moins d’accord, etc. sont généralement considérées comme des variables à intervalles, bien que cela ne soit pas tout à fait adéquat.
Les types de données ne sont pas les seules contraintes techniques pour le choix d’une procédure statistique: la taille d’échantillon et les hypothèses relatives aux données sont d’autres contraintes. Nous allons à présent nous intéresser aux hypothèses relatives aux données. Outre leurs types de données, de nombreux types d’analyse statistique fonctionnent uniquement pour des ensembles de distributions de données et des relations entre des variables spécifiques. D’un point de vue pratique, cela signifie que vous devez non seulement adapter vos techniques d’analyse aux types de mesure, mais également respecter (en gros) d’autres hypothèses relatives aux données.
La linéarité
Selon une hypothèse fréquente, les relations entre variables seraient linéaires.
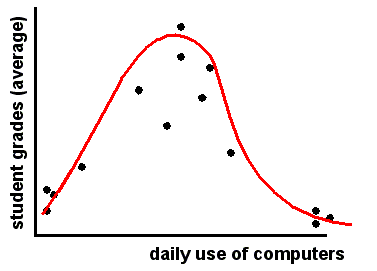
Dans la figure ci-dessous, la relation est non-linéaire: les étudiants qui ont un faible usage quotidien de leur ordinateur ont de mauvaises notes, tout comme ceux qui utilisent beaucoup leur ordinateur. Les mesures couramment utilisées telles que la corrélation de Pearson ne fonctionnent pas, i.e. elles montrent une corrélation très faible: vous passerez à côté de cette relation non-linéaire.
Distribution normale
La plupart des méthodes pour des données à intervalles nécessitent également une distribution normale (voir le chapitre précédent sur les statistiques descriptives). Si vos données incluent des « cas extrêmes » et/ou sont biaisées (asymétriques), certaines données individuelles ont bien plus de poids que les autres.
Exemple hypothétique :
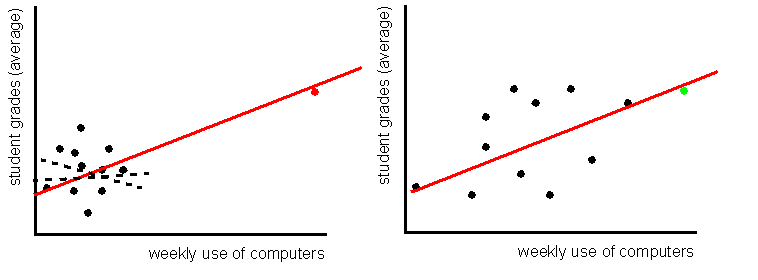
En raison du cas extrême de l’étudiant dans le graphique de gauche (point rouge) qui passe de nombreuses heures sur son ordinateur, nous obtenons une corrélation positive et un taux de régression positif, alors que tous les autres points suggèrent une absence de corrélation. Dans ce cas, l’utilisation moyenne de l’ordinateur ne représente pas une utilisation « type », car l’étudiant « rouge » tire la moyenne « vers le haut ».
Le cas extrême de l’étudiant dans le graphique de droite (point vert) n’a pas un impact important sur le résultat, car les autres données sont bien réparties sur les deux axes. Dans ce deuxième cas, la moyenne représente un étudiant type.
En outre, vous devez également comprendre que les valeurs extrêmes ont déjà plus de poids avec des méthodes d’analyse fondées sur la variance (i.e. analyse de régression, analyse de la variance, analyse des facteurs, etc.), car les distances sont calculées en tant que carrés.