STIC:STIC IV (2015)/Cubricks
Description
| Je souhaite réaliser un cube à assembler à la manière d'un tetris en 3D.
Le but est d'entrainer, par la manipulation des différentes pièces, la rotation mentale et la compréhension de la géométrie, en sollicitant des emboîtages selon des angles, des arêtes, et des surfaces définies, lors d'un cours de géométrie pour les petits. Chaque unité cubique créée peut devenir la base de construction d'unités plus grandes (comme un maçon, l'enfant fabrique ses briques (cubes) pour construire ensuite un ouvrage plus grand). |
Public cible
Le Cubricks s'adresse à des enfants de classe de 5p à 8p, de 9 à 12 ans. Selon le Plan d'Etude Romand (PER) cet objet pourrait s'inscrire dans une activité plutôt ludique en lien avec les cours de Mathématiques et Sciences de la nature, notion de repérage dans l'Espace du Cycle 2:
MSN 21 — Poser et résoudre des problèmes pour structurer le plan et l'espace…
- en imaginant et en utilisant divers outils de représentation
- en menant des observations répétées
- en se référant à diverses sources
- en triant et organisant des données
- en confrontant et en communiquant ses observations, ses résultats, ses constats, ses interprétations
- en mobilisant, selon la situation, la mesure et/ou des outils mathématiques
- en se posant des questions et en exprimant ses conceptions
Progression des apprentissages: Éléments pour la résolution de problèmes géométriques en lien avec le repérage, ainsi que les figures et les transformations étudiées:
- tri et organisation des informations
- mise en œuvre d'une démarche de résolution
- ajustement d'essais successifs
- pose d'une conjecture, puis validation ou réfutation
- déduction d'une ou plusieurs informations nouvelles à partir de celles qui sont connues
- vérification, puis communication d'une démarche et d'un résultat en utilisant un vocabulaire ainsi que des symboles adéquats
Attentes fondamentales: résolution des problèmes géométriques en faisant appel à une ou plusieurs des composantes suivantes :
- choix et mise en relation des données nécessaires à la résolution
- mobilisation de propriétés de figures et de transformations
- utilisation d'un système de repérage pour situer des objets dans le plan
- utilisation d'outils de construction appropriés
- vérification de la pertinence du résultat
- communication de la démarche et du résultat en utilisant un vocabulaire adéquat
Bases théoriques
Il s'agit d'un objet d'apprentissage physique, conçu pour promouvoir l'apprentissage à travers les interactions et peut être utilisé en milieu scolaire et à la maison. Il tente de s'inscrire dans la logique des objets d'apprentissage constructionnistes selon différents auteurs (éléments basés sur le texte de référence):
- la connaissance découle de l'expérience (John Locke, 1690)
- l'éducation est possible à travers les entraînements sensoriels et la stimulation (Itard, 1962)
- l'élève tire ses propres conclusions basées sur ses propres expériences avec une importance pour l'éducation individualisée (Rousseau, 1762)
- Selon Froebel and Montessori, il est important d'utiliser des objets qui sont cohérent avec le niveau de développement de l'apprenant, qui sont hautement modulables et qui permettent des interactions sensorielles. Les catégories de Froebel déterminent l'importance que peuvent représenter les kit de construction car ils aident l'apprenant à comprendre le monde physique et à s'engager dans une activité d'expression de leur propres idées. Les artefacts de Froebel permettent par exemple d'apprendre la géométrie de manière indirecte; c'est en construisant et assemblant des bloques différents que l'apprenant va inférer des lois géométriques.
Réalisation
Maquettage
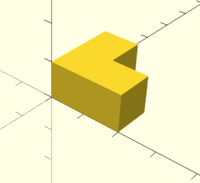
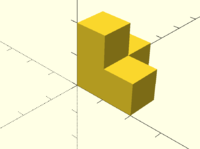
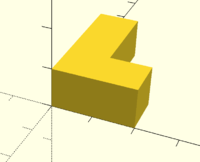
J'ai créé une maquette constituée de 27 unités cubiques de base formant le cube final. Cela m'a permis de décomposer petit à petit mon cube, et ainsi de déterminer la forme de sept pièces nécessaires à la résolution du puzzle 3D.
Caractéristiques
Le kit est constitué de sept pièces.
J'ai réalisé un cube de 3 cm3, c'est-à-dire qu'une arrête mesure 3 cm de long. C'est un cube en 3 par 3, il est donc composé de 3 unités de longueurs de 1 cm. Je voulais que chaque pièces soit différentes (pas de doublons).
J'ai été contraint pour l'impression 3d de bien penser à la forme de mes pièces. En effet, il était important d'avoir des formes régulières et lisse pour permettre un emboitement optimal. C'est pourquoi je ne voulais pas utiliser de mèches pour tenir des parties qui auraient du être "imprimée dans le vide". Je ne pouvais donc pas utiliser de formes trop biscornues et j'ai du les orienter correctement pour trouver l'angle d'impression le plus approprié.
Fichiers
fichiers openscad
fichiers stl
Production
Impression 3D
- Lieu: Uni Pignon
- Imprimante: Felix 2.0
- Plastique: rouge
- Temps: environ 1h10 (et à peu près entre huit et dix minutes par pièce)
- Quantité: les sept pièces simultanément
- Température lit: 55°
- Température extruder: 200°
- Ventilateur: 100%
- Positionnement et réparations: pas besoin
- Logiciel de commande: Repetier-Host
- Trancheur (slicer): SFACT
Statut
- Statut d'impression: terminé
Mes 7 pièces ont correctement été imprimées.
Règles
Le but du kit est de reconstituer un cube en imbriquant les pièces entre-elles. Il est obligatoire d'utiliser toutes les pièces du puzzle. Il existe plusieurs solutions possibles... Quelle sera la votre?
Il est possible de se servire de la maquette virtuelle animée, réalisée avec le logiciel d'édition de jeux vidéo "Craftstudio",
comme mode d'emploi dynamique et découvrir des indices précieux pour la résolution du kit pédagogique.
vidéo solution (cliquer sur la zone de vidéo, puis pressez la touche espace du clavier pour lancer l'animation)
Test utilisateur
- Age: 11 ans
- Niveau scolaire: 8p
- sexe: Home
- niveau en maths et géométrie: ok
- temps de résolution: 30min
Méthodologie
Passation individuelle. Dans une zone tranquille de la classe, le participant est assis à une table, sur laquelle sont présentées les sept pièces du cube à assembler. La consigne suivantes lui est donnée: « tu dois assembler ces pièces afin de former un cube. Attention, tu dois te servir de toutes les pièces, tu peux avancer à ton rythme et faire autant d’essai que tu veux. Je reste à côté et suis disponible si tu as des questions.» Ensuite l’enseignant lui demande s’il a compris et s’il a des questions. La passation débute car tout est claire pour l’enfant.
1ère phase: exploration et manipulation sans intervention de l’enseignant.
2ème phase: explicitation des stratégies par l’élève pendant la résolution + Aides éventuelles de l'enseignant
3ème phase: discussion.
Connaissances préalables
- La classe est en train d’étudier le thème huit de mathématique (cf. PER): Les surfaces et les solides (ils sont en trains de voir les propriétés des quadrilatères, des formes en trois dimensions et des cubes en particulier.)
- Il adore les casse-têtes et dit en résoudre parfois grâce à une application sur le téléphone à sa mère.
Passation
Stratégie de résolution:
- Il fait des groupes d'emboitement de 2 pièces et ensuite mettre ensemble les groupes.
- Il explique qu'il essai de voir quel pièces s'emboitent entre-elles
- Il persiste dans des stratégies non-productives.
commentaire: Il faisait souvent les mêmes stratégies non productive sans s'en rendre compte, il dit qu'il ne se souvient plus de ce qu'il a pu faire avant.
Difficultés:
- Il finissait tout le temps le cube mais avec un trou et une pièce qui dépasse et se sentait découragé.
- Il défait tout et recommence à zéro.
- Ne comprend pas que c'est un cube trois par trois et faisait des colonnes hautes ou lignes trop longues.
Aide de l’enseignant: "Qu’est ce qu’un cube?" l'enseignant explique ce qu'est un cube et lui montre ces erreurs. Il comprend que ce n'est pas la même longueur partout et que ça ne peut pas marcher ainsi.
Aide de l’enseignant: "Tu penses que le cube est de combien sur combien?" le participent avait du mal à répondre alors l'enseignant dit: "de 3 sur 3". Le participant répond que c’est logique et que ça va beaucoup l'aider de savoir ça. Il ajoute "maintenant, je connais la hauteur et la largeur maximum"
commentaire:les pièces (6 et 7) sont considérées comme étant les plus complexe. Le participant ne savait pas où les mettre alors il les gardait pour la fin. Il se justifie en disant qu’il n’a jamais vu ce genre de pièces et cite le jeu Tetris. Puis, en les manipulant, il parvient à s’y habituer et elles ne présentent plus de difficulté particulière pour lui.
Évolution des stratégies:
(après quelques minutes) :
- Essai de trouver ou les pièces peuvent aller (dans un coin, au centre etc.)
- Quand il voyait que ça ne jouait pas il essayait de remplacer une pièce en gardant une base sans tout défaire.
Évaluation du cube
Q: Penses-tu que cet exercice est utile pour comprendre la géométrie ?
R: Oui parce qu'on arrive mieux à se rendre compte de la troisième dimension et des propriétés du cube
Q: Qu'as-tu appris ?
R: j'ai pu me souvenir de notions qu'on a déjà vu comme les propriétés du cube MAIS AUSSI que lors d'une tâche comme celle-ci, il ne faut pas se lancer sans réfléchir et faire au hasard. Il faut avoir des stratégies et se souvenir des combinaisons déjà effectuées.
Q: Qu'as-tu trouvé de difficile ?
R: Trouver les bons emboîtements et la disposition dans le cube ET ne pas se laisser décourager notamment quand on y est presque (en référence avec le cube avec un trou et une pièce qui dépasse)
Q: Qu'as-tu trouvé de facile?
R: les pièces sont faciles à manipuler. le nombre de pièces est bien car plus de pièces aurait ajouté de la difficulté. La taille des pièces est bien, car les casse-tête qu'il résoud sont de cette taille, ajoute-t-il. Il dit: "Je préfère résoudre des casse-tête en vrai car c'est plus concret qu'avec des applications sur le natel." Il précise qu'il se représente mieux la 3D ainsi.
Q: As-tu apprécié travailler avec l'objet?
R: Oui cela m'a beaucoup intéressé de travailler différemment.
Q: Aurais-tu besoin d'autres aides que l'enseignant?
R: D'avoir plus d'indices sur la disposition des pièces ET peut-être pouvoir dessiner les étapes afin de ne pas refaire les mêmes combinaisons.
References
- imprimante 3D Felix 2.0 Tuto
- Plan d'Etude Romand
- Zuckerman, Oren (2006, in preparation), Historical Overview and Classification of Traditional and Digital Learning Objects MIT Media Laboratory, 20 Ames Street, Cambridge, MA 02139.